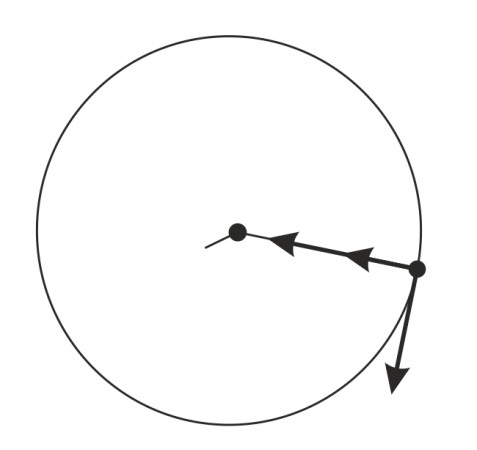
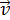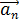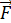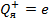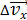Энергия электрона в атоме водорода.
Энергия электрона представляет собой сумму кинетической энергии 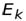 и потенциальной
и потенциальной 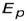 .
.
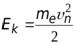 и
и 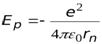 .
.
Потенциальная энергия – это энергия электрона с зарядом 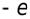 в электрическом поле ядра. Из уравнения (4) видно, что
в электрическом поле ядра. Из уравнения (4) видно, что
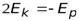 .
.
Тогда на n –ой орбите энергия электрона равна
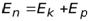 =
= 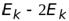 =
=  .
.
Т.е. кинетическая энергия электрона равна полной энергии, взятой со знаком «-».
Также полную энергию можно записать через потенциальную:
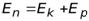 =
= 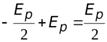 , или
, или
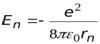 .
.
Подставим 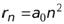 . Тогда
. Тогда
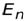 =
= 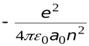 .
.
Энергия на первой орбите (на первом энергетическом уровне) равна
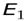 =
= 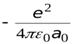 = -13,6 эВ.
= -13,6 эВ.
Величину 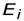 = 13,6 эВ = 2,18∙10-18 Джназываютэнергией ионизации (эта энергия необходима, чтобы перевести электрон, находящийся на первом уровне, в свободное состояние, т.е. чтобы ионизовать атом). Окончательно, энергия электрона на n –ом энергетическом уровне (на n –ой орбите) записывается как
= 13,6 эВ = 2,18∙10-18 Джназываютэнергией ионизации (эта энергия необходима, чтобы перевести электрон, находящийся на первом уровне, в свободное состояние, т.е. чтобы ионизовать атом). Окончательно, энергия электрона на n –ом энергетическом уровне (на n –ой орбите) записывается как
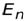 =
= 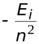 .
.
Спектр излучения водорода.
Энергия излучаемого или поглощаемого кванта:
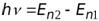 .
.
Частота 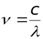 ,
, 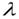 длина волны,
длина волны, 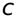 - скорость света в вакууме.
- скорость света в вакууме.
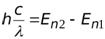 =
= 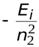 +
+ 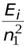 =
= 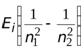 ,
,
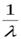 =
= 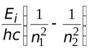 .
.
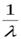 =
= 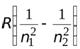 - формула Бальмера,
- формула Бальмера,
определяет длины волн в спектре атома водорода.
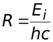 = 1,1∙107 м-1 - постоянная Ридберга.
= 1,1∙107 м-1 - постоянная Ридберга.
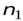 и
и 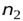 - номера энергетических состояний (номера орбит) электрона.
- номера энергетических состояний (номера орбит) электрона.
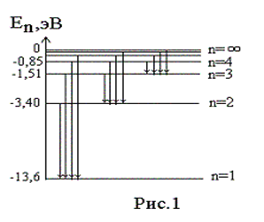
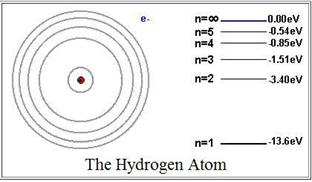
Переходы электрона с возбужденных энергетических состояний на основной энергетический уровень ( 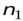 = 1) сопровождаются излучением вУФ области спектра (серия линий Лаймана),
= 1) сопровождаются излучением вУФ области спектра (серия линий Лаймана),
переходы на уровень с 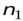 = 2 приводят к линиямв видимой области (серия Бальмера),
= 2 приводят к линиямв видимой области (серия Бальмера),
переходы на уровень с 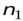 = 3, 4, 5, … приводят излучению вИК области.
= 3, 4, 5, … приводят излучению вИК области.
Теория Бора не смогла объяснить строение сложных атомов. Для объяснения поведения микрочастиц была развита квантовая механика.
Она основана на том, что любая микрочастица, наряду с корпускулярными, обладает также волновыми свойствами (гипотеза де Бройля).
Для фотона, импульс
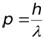 .
.
По аналогии с фотоном, любую микрочастицу можно рассматривать как волну с длиной волны
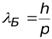 ,
,
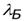 - длина волны де Бройля.
- длина волны де Бройля.
Гипотеза де Бройля подтверждена экспериментально наблюдением дифракции электронов, а затем и протонов.
Принцип неопределенностей.
Первая попытка создания на основе накопленных экспериментальных данных модели атома принадлежит Дж. Дж. Томсону (1903). Согласно этой модели, атом представляет собой непрерывно заряженный положительным зарядом шар радиусом порядка 10-10 м, внутри которого около своих положений равновесия колеблются электроны; суммарный отрицательный заряд электронов равен положительному заряду шара, поэтому атом в целом нейтрален. Через несколько лет было доказано, что представление о непрерывно распределенном внутри атома положительном заряде ошибочно.
Рис. 3.6
В развитии представлений о строении атома велико значение опытов английского физика Э. Резерфорда (1871 —1937) по рассеянию a-частиц в веществе. Альфа-частицы возникают при радиоактивных превращениях; они являются положительно заряженными частицами с зарядом 2е и массой, примерно в 7300 раз большей массы электрона. Резерфорд, исследуя прохождение a-частиц в веществе, показал, что основная их часть испытывает незначительные отклонения, но некоторые a-частицы (примерно одна из 20 000) резко отклоняются от первоначального направления (углы отклонения достигали даже 180°). Резерфордом был сделан вывод, что значительное отклонение a-частиц обусловлено их взаимодействием с положительным зарядом большой массы, которая сосредоточен в объеме, очень малом по сравнению с объемом атома.
На основании своих исследований Резерфорд в 1911 г. предложил ядерную (планетарную) модель атома. Согласно этой модели, вокруг положительного ядра, имеющего заряд Ze (Z — порядковый номер элемента в системе Менделеева, е — элементарный заряд), размер 10-15- 10-14 м и массу, практически равную массе атома, в области с линейными размерами порядка 10-10 м по замкнутым орбитам движутся электроны, образуя электронную оболочку атома. Так как атомы нейтральны, то заряд ядра равен суммарному заряду электронов, т. е. вокруг ядра должно вращаться Z электронов.
Однако электрон, движущийся ускоренно по окружности под действием кулоновской силы, согласно электродинамике, должен излучать электромагнитные волны и вследствие этого непрерывно терять энергию. В результате электрон будет приближаться к ядру и в конце концов упадет на него. Атом Резерфорда, с точки зрения классической физики, оказывается неустойчивой системой, что противоречит действительности.
Первая попытка построить качественно новую — квантовую — теорию атома была предпринята в 1913 г. датским физиком Нильсом Бором. Он поставил перед собой цель связать в единое целое эмпирические закономерности линейчатых спектров, ядерную модель атома Резерфорда и квантовый характер излучения и поглощения света.
Чтобы объяснить устойчивость атома датский физик Нильс Бор постулировал основные положения (постулаты Бора), которые явили собой первую квантовую модель атома.
 Постулаты Бора:
Постулаты Бора:
1. Электроны в атоме движутся по некоторым стационарным орбитам. Движение электронов по стационарным орбитам не сопровождается излучением электромагнитных волн.
2. В стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь дискретные квантованные значения момента импульса, удовлетворяющие условию квантования момента импульса электрона
Рис.3.7
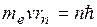 (3.5.1)
(3.5.1)
n = 1,2,3…– главное квантовое число (номер орбиты-уровня), me - масса элетрона, v — его скорость на n-ой орбите радиуса rn, 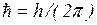 , h = 6,62·10-34 Дж·с – постоянная Планка;
, h = 6,62·10-34 Дж·с – постоянная Планка;
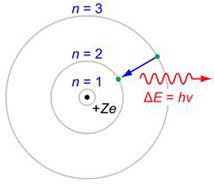
3. При переходе электрона с одной стационарной орбиты на другую излучается (поглощается) один фотон с энергией:
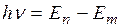 (3.5.2)
(3.5.2)
равной разности энергий соответствующих стационарных состояний (Еn и Еm — соответственно энергии стационарных состояний атома до и после излучения (поглощения). При Еn>Еm происходит излучение фотона (переход атома из состояния с большей энергией в состояние меньшей энергией, т. е. переход электрона с более удаленной от ядра орбиты на более близлежащую), при Еn<Еm — его поглощение (переход атома в состояние большей энергией, т. е. переход электрона на более удаленную от ядра орбиту). Набор возможных дискретных частот
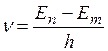 (3.5.3)
(3.5.3)
квантовых переходов определяет линейчатый спектр атома. Излучение атома представляет не непрерывный спектр, а спектр, состоящий из отдельных линий, соответствующих определенным частотам.
Используя постулаты Бора, закон Кулона и вращение электрона по круговой орбите, можно рассчитать величину радиуса орбиты rn и скорость электрона на ней vn:
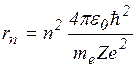 n=1,2,3… (3.5.4)
n=1,2,3… (3.5.4)
, (3.5.5)
где m – масса электрона;
ε0 – электрическая постоянная:
z – порядковый номер элемента;
е – заряд ядра.
Полная энергия Е орбитального электрона равна сумме его кинетической и потенциальной энергий:
Еn = Екинn + Епотn
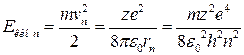
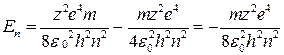 (3.5.6)
(3.5.6)
Для атома водорода (Z=1) радиус первой орбиты электрона при n=1, называемый первым боровским радиусом, равен r1 = 0,528 10-10 м. Энергия электрона в водородоподобном атоме может принимать следующие дискретные значения:
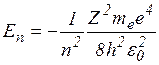 n=1,2,3… (3.5.7)
n=1,2,3… (3.5.7)
Полная энергия электрона в атоме – величина отрицательная (Еn<0), т.е. электроны в атоме движутся как в потенциальной яме.
Электроны, находясь на стационарных орбитах, обладают потенциальной энергией, максимальная величина которой будет ¥, то есть будет соответствовать ионизованному атому. Там она будет равна нулю, следовательно, потенциальная энергия электрона в атоме отрицательна.
Целое число n в выражении, определяющее энергетические уровни атома, называется главным квантовым числом. Энергетический уровень с n = 1 является основным (нормальным); состояния с n>1 являются возбужденными.
Из представленных выше формул можно получить выражение для частоты излучения при переходе электрона с одного энергетического уровня на другой
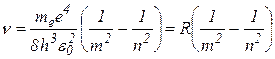
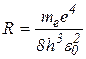 (3.5.8)
(3.5.8)
R – постоянная Ридберга, для атома водорода R=3.29 1015 c-1.
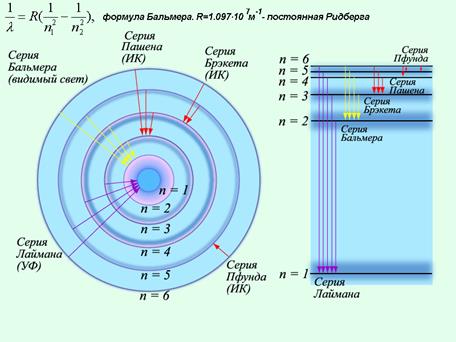
Рис. 3.8.
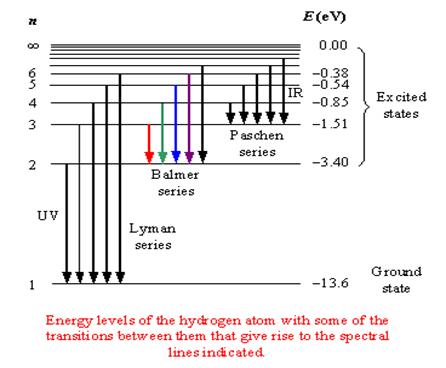
При переходе электрона с произвольного возбужденного уровня на уровень с фиксированным значением m получим набор частот (группу линий в спектре атома) который называется серией. Так в атоме водорода переход на основной уровень (m=1) c произвольного возбужденного уровня (n=2,3,4…) определяет серию Лаймана; переход на уровень с m=2 c уровня n=3,4,5… определяет серию Бальмера; переход на уровень с m=3 c уровня n=4,5,6… определяет серию Пашена и т.д.
Переход с более удаленной орбиты на более близкую связан с испусканием одного фотона – такова причина возникновения линейчатого спектра испускания, а переход электрона на более дальнюю орбиту при поглощении фотона соответствует возникновению линейчатогоспектра поглощения.
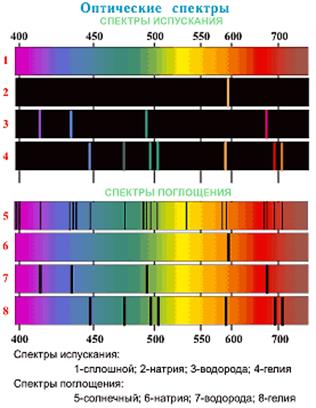 Атомные спектры обладают ярко выраженной индивидуальностью, причем их вид определяется не только атомом данного элемента, но и его строением, внешними факторами: температурой, давлением, электрическими и магнитными полями и др.
Атомные спектры обладают ярко выраженной индивидуальностью, причем их вид определяется не только атомом данного элемента, но и его строением, внешними факторами: температурой, давлением, электрическими и магнитными полями и др.
Получение и анализ спектров играют огромную роль в теоретической и прикладной физике и технике. Изучение спектров испускания и поглощения веществ позволяет установить энергетические уровни и тончайшие детали строения атомов. Знание же спектров атомов и молекул различных химических соединений позволяет проводить спектральный анализ, т.е. устанавливать состав исследуемых тел.
План решения задач по теме «Теория атома водорода по Бору»
1. Следует обратить внимание, что созданная Бором теория атома водорода – первая квантовая теория атома, согласно которой электрон в атоме может находиться только в определенных стационарных состояниях. Параметры электрона в атоме: радиус круговой орбиты, скорость и его момент импульса, период обращения, энергия электрона, – имеют в этих состояниях дискретные значения, которые определяются главным квантовым числом 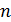 (номер орбиты). Эта зависимость отражается индексом величин:
(номер орбиты). Эта зависимость отражается индексом величин: 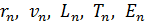 .
.
2. По мере увеличения номера орбиты 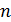 ее радиус увеличивается
ее радиус увеличивается 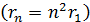 , а скорость электрона уменьшается
, а скорость электрона уменьшается 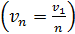 ; в результате период обращения растет
; в результате период обращения растет 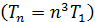 , возрастает момент импульса электрона
, возрастает момент импульса электрона 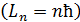 и увеличивается его энергия
и увеличивается его энергия 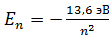 .
.
3. Порядок величин параметров электрона в атоме водорода можно оценить по указанным зависимостям и значениям величин для основного состояния 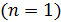 . В этом состоянии радиус орбиты
. В этом состоянии радиус орбиты 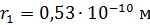 , скорость электрона
, скорость электрона 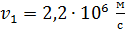 , период обращения
, период обращения 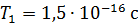 , момент импульса
, момент импульса 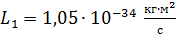 , и полная энергия электрона
, и полная энергия электрона 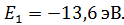
Задача 30. Для электрона, находящегося на первой орбите ( 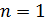 ) атома водорода, определите радиус орбиты
) атома водорода, определите радиус орбиты 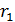 , момент импульса электрона
, момент импульса электрона 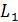 и его скорость
и его скорость 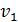 .
.
Дано Электрон в атоме 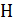 : : 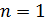 . . 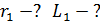 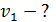 | Решение По теории Бора электрон в атоме водорода движется по окружности радиусом 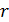 . На орбите электрон удерживается кулоновской силой . На орбите электрон удерживается кулоновской силой 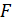 притяжения к ядру, имеющему положительный заряд. Эта сила создает нормальное (центростремительное) ускорение, которое, в соответствии со вторым законом Ньютона: притяжения к ядру, имеющему положительный заряд. Эта сила создает нормальное (центростремительное) ускорение, которое, в соответствии со вторым законом Ньютона: |
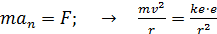 . (1)
. (1)
Здесь 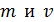 – масса и скорость электрона;
– масса и скорость электрона; 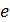 – заряд электрона и ядра (
– заряд электрона и ядра ( 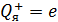 );
); 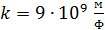 – коэффициент пропорциональности в законе Кулона.
– коэффициент пропорциональности в законе Кулона.
В уравнении (1) две неизвестные величины: 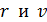 . Другое уравнение, которое также содержит эти величины, – первый постулат Бора, определяющий условие квантования момента импульса электрона:
. Другое уравнение, которое также содержит эти величины, – первый постулат Бора, определяющий условие квантования момента импульса электрона:
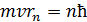 . (2)
. (2)
Здесь 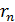 – радиус -ой стационарной орбиты;
– радиус -ой стационарной орбиты; 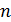 – главное квантовое число;
– главное квантовое число; 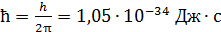 – постоянная Планка.
– постоянная Планка.
Выразим из уравнения (2) скорость электрона:
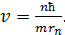 (3)
(3)
Подставим это значение скорости 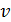 в уравнение (1) и определим из него радиус -ой орбиты электрона:
в уравнение (1) и определим из него радиус -ой орбиты электрона:
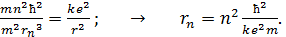 (4)
(4)
Полученную формулу представим в следующем виде:
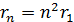 , (5)
, (5)
где 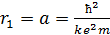 – первый боровский радиус.
– первый боровский радиус.
Вычисляем величину радиуса первой орбиты электрона в атоме водорода:
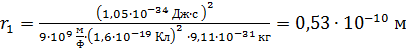 .
.
Момент импульса электрона 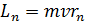 вычисляем по уравнению (2) первого постулата Бора:
вычисляем по уравнению (2) первого постулата Бора:
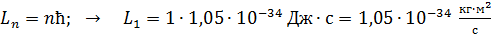 .
.
Скорость электрона на первой орбите в атоме водорода определим по величине момента импульса электрона (согласно уравнению (3)):
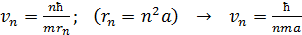 . (6)
. (6)
Вычисляем скорость электрона на первой орбите в атоме водорода:
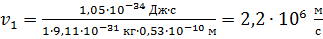 .
.
Задача 31.Для электрона, находящегося на третьей орбите ( 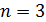 ) атома водорода, определите радиус орбиты
) атома водорода, определите радиус орбиты 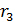 , скорость электрона на этой орбите
, скорость электрона на этой орбите 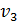 и период его обращения
и период его обращения 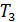 .
.
Дано Электрон в атоме 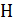 : : 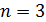 . . 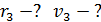 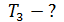 | Решение Запишем второй закон Ньютона для движения электрона по окружности радиусом 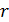 вокруг ядра атома водорода, заряд которого вокруг ядра атома водорода, заряд которого 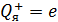 (рис. 51). Сила Кулона (рис. 51). Сила Кулона 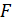 направлена по радиусу окружности к ее центру и является центростремительной, поэтому уравнение закона Ньютона запишем в проекции на нормаль к траектории: направлена по радиусу окружности к ее центру и является центростремительной, поэтому уравнение закона Ньютона запишем в проекции на нормаль к траектории: |
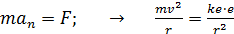 . (1)
. (1)
Здесь 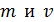 – масса и скорость электрона;
– масса и скорость электрона; 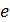 – заряд электрона и ядра;
– заряд электрона и ядра; 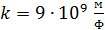 – кулоновская постоянная в системе единиц СИ.
– кулоновская постоянная в системе единиц СИ.
Рис. 51 | Так как уравнение (1) содержит две неизвестные величины: скорость 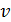 движения электрона и радиус его орбиты движения электрона и радиус его орбиты 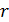 , – то используем еще одно уравнение, которое связывает эти величины, – первый постулат Бора (условие квантования момента импульса электрона): , – то используем еще одно уравнение, которое связывает эти величины, – первый постулат Бора (условие квантования момента импульса электрона): 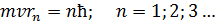 . (2) Выразим скорость электрона из уравнения (2), подставим ее значение в уравнение (1), и определим из него радиус -ной стационарной орбиты . (2) Выразим скорость электрона из уравнения (2), подставим ее значение в уравнение (1), и определим из него радиус -ной стационарной орбиты 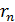 : : |
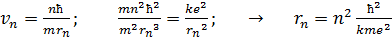 . (3)
. (3)
Формулу (3) представим в следующем виде:
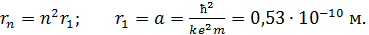 (4)
(4)
Здесь 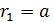 – первый боровский радиус (согласно формуле (4)
– первый боровский радиус (согласно формуле (4) 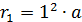 ). Вычисляем радиус
). Вычисляем радиус 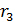 третьей боровской орбиты электрона в атоме водорода:
третьей боровской орбиты электрона в атоме водорода:
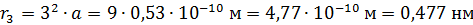 .
.
Вычисляем скорость электрона на третьей орбите, используя первый постулат Бора, по формуле (3):
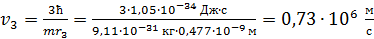 .
.
Период обращения 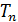 электрона на -ной орбите: время одного оборота, – определим по формуле пути
электрона на -ной орбите: время одного оборота, – определим по формуле пути 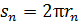 для равномерного движения электрона со скорость
для равномерного движения электрона со скорость 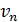 :
:
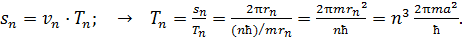 (5)
(5)
Формулу (5) представим в следующем виде:
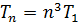 , (6)
, (6)
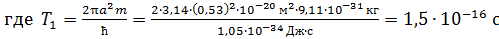 , – период обращения электрона на первой орбите.
, – период обращения электрона на первой орбите.
Вычисляем период обращения электрона на третьей боровской орбите атома водорода по формуле (6):
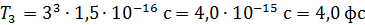 .
.
Полученная величина периода обращения 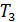 показывает, что число оборотов в одну секунду, которое совершает электрон при движении в поле ядра атома водорода:
показывает, что число оборотов в одну секунду, которое совершает электрон при движении в поле ядра атома водорода: 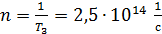 .
.
Задача 32.Для атома водорода определите 1) полную энергию электрона 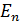 на орбитах с главным квантовым числом
на орбитах с главным квантовым числом 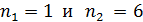 и 2) длину волны λ фотона, излучаемого при переходе электрона с шестого энергетического уровня на первый – в серии Лаймана (ультрафиолетовой).
и 2) длину волны λ фотона, излучаемого при переходе электрона с шестого энергетического уровня на первый – в серии Лаймана (ультрафиолетовой).
Дано Электрон в атоме 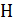 : : 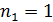 ; ; 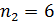 . . 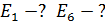 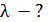 | Решение Полная энергия 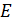 электрона в атоме водорода (и в любом другом атоме) равна сумме кинетической энергии электрона в атоме водорода (и в любом другом атоме) равна сумме кинетической энергии 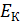 электрона и потенциальной энергии его взаимодействия с зарядом ядра электрона и потенциальной энергии его взаимодействия с зарядом ядра 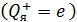 : : 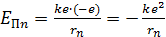 . Таким образом, величина полной энергии . Таким образом, величина полной энергии 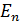 атома водорода в состоянии с главным квантовым числом атома водорода в состоянии с главным квантовым числом 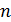 |
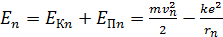 . (1)
. (1)
Здесь 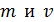 – масса электрона и его скорость на -ной орбите;
– масса электрона и его скорость на -ной орбите; 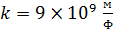 – кулоновская постоянная в системе единиц СИ;
– кулоновская постоянная в системе единиц СИ; 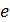 – заряд электрона и ядра
– заряд электрона и ядра 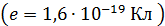 ;
; 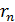 – радиус орбиты с номером
– радиус орбиты с номером 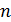 .
.
Скорость электрона определим из закона динамики движения по круговой орбите (из второго закона Ньютона, записанного в проекции на нормаль):
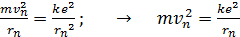 . (2)
. (2)
Подставим найденное значение 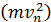 в формулу энергии электрона (1):
в формулу энергии электрона (1):
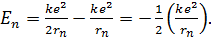 (3)
(3)
Сравнивая уравнения (1) и (3), отметим соотношение энергий электрона, движущегося в атоме водорода:
1) потенциальная энергия 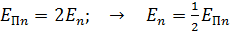 ;
;
2) кинетическая энергия 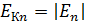 .
.
Полная энергия 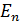 электрона в атоме отрицательна; это означает, что электрон находится в связанном состоянии благодаря электростатическому взаимодействию с заряженным ядром атома.
электрона в атоме отрицательна; это означает, что электрон находится в связанном состоянии благодаря электростатическому взаимодействию с заряженным ядром атома.
Для получения расчетной формулы полной энергии электрона 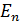 в формулу (3) подставим значение радиуса орбиты
в формулу (3) подставим значение радиуса орбиты 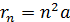 ; при этом энергия электрона в состоянии с главным квантовым числом
; при этом энергия электрона в состоянии с главным квантовым числом 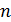
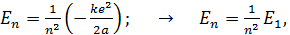 (4)
(4)
где 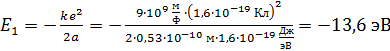 – энергия электрона в состоянии с квантовым числом
– энергия электрона в состоянии с квантовым числом 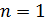 (одна из искомых величин). Величина
(одна из искомых величин). Величина 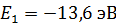 является минимальной энергией, которой обладает атом водорода в основном состоянии (
является минимальной энергией, которой обладает атом водорода в основном состоянии ( 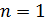 ). Максимальная энергия (согласно формуле (4)
). Максимальная энергия (согласно формуле (4) 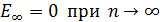 ) соответствует ионизации атома путем отрыва электрона от ядра.
) соответствует ионизации атома путем отрыва электрона от ядра.
Вычислим по формуле (4) энергию атома в возбужденном состоянии, соответствующем движению электрона по шестой стационарной орбите:
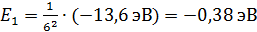 .
.
Чтобы определить длину волны фотона, испускаемого при переходе электрона с 6-го энергетического уровня на 1-й, используем второй постулат Бора: при переходе электрона с одной стационарной орбиты на другую излучается фотон с энергией, равной разности энергий электрона на этих орбитах:
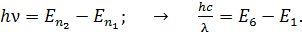 (5)
(5)
Уравнение (5) дает следующую расчетную формулу длины волны излучаемого фотона:
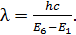 (6)
(6)
Вычисляем по этой формуле длину волны спектральной линии, соответствующей переходу электрона в атоме водорода с 6-й стационарной орбиты на 1-ю (в основное состояние):
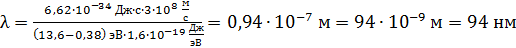 .
.
Это длина волны ультрафиолетового (УФ) излучения, так как величина 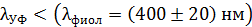 .
.
План решения задач по теме «Элементы квантовой механики»
1. Длина волны де Бройля для частиц вычисляется по формуле 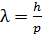 , где импульс частицы
, где импульс частицы 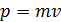 . Если известна кинетическая энергия частицы
. Если известна кинетическая энергия частицы 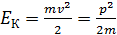 , то импульс выражают через энергию:
, то импульс выражают через энергию: 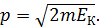
Если заряженная частица (электрон, протон, 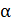 -частица) ускорена электрическим полем, совершившим работу
-частица) ускорена электрическим полем, совершившим работу 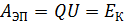 , то кинетическая энергия определяется величиной ускоряющей разности потенциалов
, то кинетическая энергия определяется величиной ускоряющей разности потенциалов 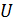 . Привычную формулу классической механики
. Привычную формулу классической механики 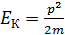 можно использовать для частиц, кинетическая энергия которых мала по сравнению с их энергией покоя
можно использовать для частиц, кинетическая энергия которых мала по сравнению с их энергией покоя 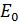 :
: 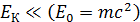 . Приведем значения энергии покоя некоторых частиц: для электрона
. Приведем значения энергии покоя некоторых частиц: для электрона 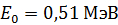 ; для протона
; для протона 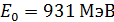 ; для
; для 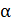 -частицы
-частицы 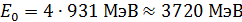 .
.
2. Длину волны де Бройля можно определить из дифракционного эксперимента, используя для параллельного пучка частиц такие же условия максимумов и минимумов дифракции, как и для потока фотонов видимого или рентгеновского излучения. Приведем эти формулы:
1) для дифракции на щели: а) условие 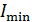 –
– 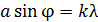 ;
;
б) условие 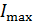 –
– 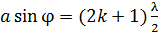 ;
;
2) для дифракции на кристалле – формула Вульфа – Брэггов:
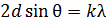 .
.
3. Для микрочастиц, находящихся в ограниченной области пространства (в атоме, в ядре, в узкой потенциальной яме), характерна ненулевая минимальная кинетическая энергия: 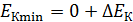 и ненулевое значение минимального импульса:
и ненулевое значение минимального импульса: 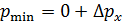 , так как такая частица, согласно соотношению неопределенностей, не может иметь точные нулевые значения. Поскольку неопределенность координаты частицы
, так как такая частица, согласно соотношению неопределенностей, не может иметь точные нулевые значения. Поскольку неопределенность координаты частицы 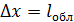 , – определяется характерным размером области, то, используя соотношение
, – определяется характерным размером области, то, используя соотношение 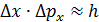 , можно получить формулу, связывающую минимальную кинетическую энергию частицы с размером области:
, можно получить формулу, связывающую минимальную кинетическую энергию частицы с размером области: 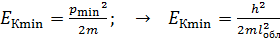 .
.
Задача 33.Электрон движется со скоростью 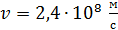 . Определите длину волны де Бройля
. Определите длину волны де Бройля 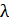 электрона, учитывая зависимость его массы от скорости.
электрона, учитывая зависимость его массы от скорости.
Дано Электрон: 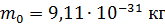 ; ; 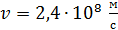 ; ;  . . 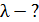 | Решение Длина волны де Бройля 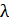 свободно движущейся частицы определяется формулой: свободно движущейся частицы определяется формулой: 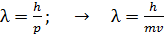 , (1) где , (1) где 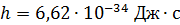 – постоянная Планка; – постоянная Планка; 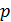 – импульс частицы; – импульс частицы; 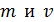 – ее масса и скорость. При скоростях, сравнимых со скоростью света – ее масса и скорость. При скоростях, сравнимых со скоростью света 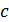 , , |
масса частиц зависит от их скорости. Увеличение массы частицы в зависимости от ее скорости 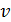 описывается формулой специальной теории относительности:
описывается формулой специальной теории относительности:
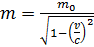 , (2)
, (2)
где 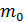 – масса покоя электрона;
– масса покоя электрона; 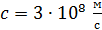 – скорость света в вакууме.
– скорость света в вакууме.
Подстановкой выражения (2) для массы электрона в формулу (1) получаем следующую расчетную формулу длины волны де Бройля релятивистского электрона:
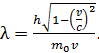 (3)
(3)
Вычисляем величину 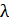 :
:
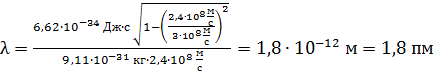 .
.
Задача 34.Электрон прошел в электростатическом поле (ЭСП) ускоряющую разность потенциалов: 1) 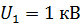 ; 2)
; 2) 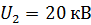 . Определите длины волн де Бройля
. Определите длины волн де Бройля 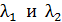 электрона при
электрона при 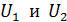 .
.
Дано Электрон: 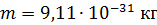 ; 1) ; 1) 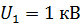 ; 2) ; 2) 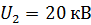 . . 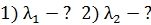 | Решение Длина волны де Бройля 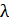 свободно движущейся частицы определяется формулой: свободно движущейся частицы определяется формулой: 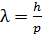 , (1) где , (1) где 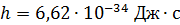 – постоянная Планка; – постоянная Планка; 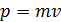 – импульс частицы; – импульс частицы; 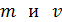 – ее масса и скорость. – ее масса и скорость. |
Пройдя в ЭСП ускоряющую разность потенциалов 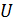 , электрон приобрел кинетическую энергию
, электрон приобрел кинетическую энергию 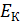 , равную работе электрического поля:
, равную работе электрического поля:
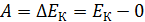 .
.
Величина работы, совершенной полем, 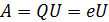 .
.
Приравнивая две последние формулы, определяем кинетическую энергию:
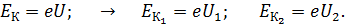 (2)
(2)
Вычисляем кинетическую энергию электрона для обоих случаев:
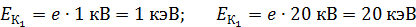 .
.
Сравним найденные величины энергии с энергией покоя электрона
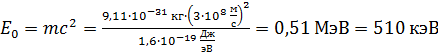 .
.
Отмечаем, что 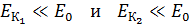 . Следовательно, электрон не является релятивистским и для его импульса и кинетической энергии справедливы формулы классической механики:
. Следовательно, электрон не является релятивистским и для его импульса и кинетической энергии справедливы формулы классической механики:
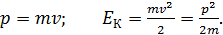 (3)
(3)
Проверим, что это так, вычислив скорость электрона при 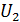 из равенства
из равенства 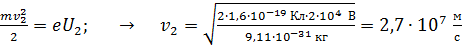 . Релятивистская поправка (множитель) в этом случае равна
. Релятивистская поправка (множитель) в этом случае равна 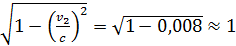 .
.
Используя для кинетической энергии формулу (2), определяем по формуле (3) импульс электрона:
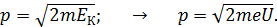 (4)
(4)
Подстановкой полученной величины импульса электрона в формулу (1) получаем следующую расчетную формулу длины волны электрона:
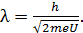 (5)
(5)
Вычисляем 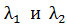 по формуле (5):
по формуле (5):
 .
.
Вычислим величину 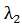 следующим путем: согласно формуле (5)
следующим путем: согласно формуле (5)
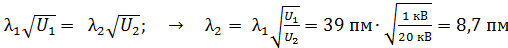 .
.
Задача 35.Параллельный пучок атомов водорода, падающий под углом скольжения 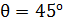 к поверхности монокристалла, дает дифракционный максимум 1-го порядка при отражении от плоскостей с межатомным расстоянием
к поверхности монокристалла, дает дифракционный максимум 1-го порядка при отражении от плоскостей с межатомным расстоянием 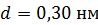 . Определите длину волны де Бройля
. Определите длину волны де Бройля 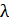 атомов водорода и их скорость
атомов водорода и их скорость 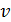 .
.
Дано Атом 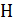 : : 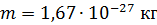 ; ; 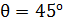 ; ; 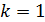 ; ; 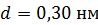 . . 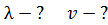 | Решение Для дифракции на кристалле легких частиц: электронов, 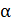 - частиц, протонов, нейтронов, атомов водорода и гелия и др., – справедлива формула Вульфа – Брэггов, полученная для дифракции рентгеновских лучей (потока фотонов): - частиц, протонов, нейтронов, атомов водорода и гелия и др., – справедлива формула Вульфа – Брэггов, полученная для дифракции рентгеновских лучей (потока фотонов): 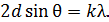 (1) Осуществляя дифракцию атомов водорода на монокристалле с известным расстоянием (1) Осуществляя дифракцию атомов водорода на монокристалле с известным расстоянием 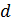 |
между атомными плоскостями, и измеряя угол скольжения 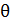 для максимума 1-го порядка, по формуле (1) определяем длину волны атомов водорода:
для максимума 1-го порядка, по формуле (1) определяем длину волны атомов водорода:
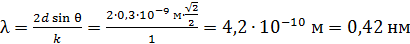 .
.
Эта величина 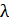 атомов водорода попадает в диапазон длин волн мягких рентгеновских лучей.
атомов водорода попадает в диапазон длин волн мягких рентгеновских лучей.
Для определения скорости атомов водорода воспользуемся формулой длины волны де Бройля свободно движущейся частицы:
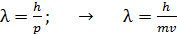 , (2)
, (2)
где 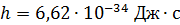 – постоянная Планка;
– постоянная Планка; 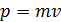 – импульс частицы;
– импульс частицы; 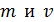 – ее масса и скорость.
– ее масса и скорость.
Из этой формулы получаем расчетную формулу скорости атомов водорода и вычисляем величину 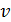 :
:
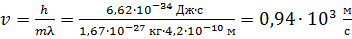 .
.
Задача 36. Электрон, имеющий кинетическую энергию 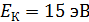 , находится в металлической пылинке диаметром
, находится в металлической пылинке диаметром 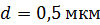 . Оцените относительную неопределенность (точность)
. Оцените относительную неопределенность (точность) 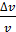 , с которой можно найти скорость электрона
, с которой можно найти скорость электрона 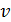 .
.
Дано Электрон: 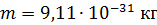 ; ; 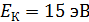 ; ; 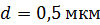 . . 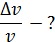 | Решение
|