Масса и импульс фотона. Световое давление.

Так как фотон обладает энергией Е=hν, то он должен иметь массу 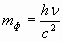. Фотон движется со скоростью света с, поэтому его импульс

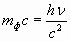(4.2.26)

Видно, что с увеличением частоты излучения ν масса и импульс фотона возрастают.

Масса фотона оказывается крайне малой, однако для жесткого рентгеновского излучения она уже сравнима с массой электрона, а для гамма-излучения даже превышает массу электрона.

Поскольку фотоны обладают импульсом, световой поток должен оказывать давление на преграды, встречающиеся на его пути. Световое давление обычно рассчитывается на основе квантовой теории, рассматривая свет как поток фотонов. Расчет дает следующее выражение для светового давления р:

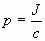(4.2.27)

где J- интенсивность монохроматического пучка света J = Nhν (N- число фотонов, падающих на площадь 1 м² за 1 с.)

Экспериментально световое давление было впервые обнаружено и измерено в 1900г П.Н.Лебедевым.

Значения светового давления, полученные Лебедевым на опыте, совпали с теоретически рассчитанными значениями. В частности оказалось, что давление света на отражающую поверхность (блестящую пластинку) вдвое больше, чем на поглощающую (зачерненную пластинку).

Эффект Комптона

Взаимодействие фотонов с электронами впервые наблюдалось на опыте в 1923г., американским физиком А.Х.Комптоном. Он обнаружил, что

При рентгеновском облучении вещества, содержащего свободные или слабо связанные электроны, происходит рассеяние рентгеновских лучей, сопровождающееся увеличением длины волны рассеянного излучения (эффект Комптона или комптоновское рассеяние).

Схема эффекта Комптона изображена на рис.4.2.8 Фотон, имеющий энергию hν₀, сталкиваясь с электроном e, передает ему часть своей энергии. В результате электрон отскакивает в сторону, а фотон изменяет направление своего движения (рассеивается). Очевидно, что энергия рассеянного фотона hν< hν₀ (поскольку часть энергии фотон передал электрону). Следовательно, ν< ν₀, а λ>λ₀ (где λ и λ₀-длины волн рассеянного и падающего фотонов)

Опыт и теории показывают, что увеличение длины волны рассеянного фотона Δλ = λ- λ₀ зависит только от угла рассеяния Θ:

Δλ = 2λкsin2(Θ/2),

(4.2.28)

где постоянная λ _к называется комптоновской длиной волны и равна

λ_к=2,43·10^-12м.

Комптоновское рассеяние, подобно фотоэффекту, не укладывается в рамки классической теории, согласно которой длина волны излучения при рассеянии остается без изменения. Если же фотон рассматривать с точки зрения квантовой теории как частицу с импульсом 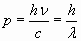и взаимодействие с электронами по закону упругого соударения, то явление получает удовлетворительное объяснение.

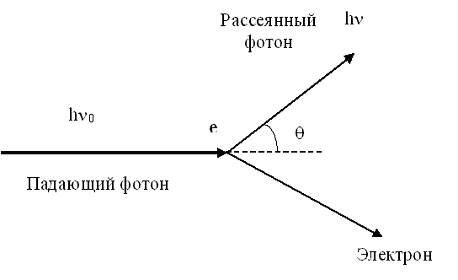
Рис.4.2.8. Схема эффекта Комптона

Модель атома Бора

Электромагнитные излучения - видимый свет, радиоволны, инфракрасное и ультрафиолетовое излучения - могут поглощаться и испускаться атомами. Этим, в частности, объясняется окраска окружающих нас тел.

Если нагреть газ, то окажется, что такое тело обладает линейчатым спектром испускания (излучаемые электромагнитные волны занимают узкие полоски в спектре). Спектром обычно называют зависимость интенсивности излучения от длины или частоты волны. Газ того или иного сорта представляет собой совокупность атомов данного вещества, слабо взаимодействующих друг с другом. Швейцарский ученый И.Бальмер установил (1885), что длины волн известных в то время девяти линий спектра водорода удовлетворяют формуле:

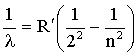(4.2.28)

где R' = 10973731,77 м^-1 - постоянная Ридберга, n = 3, 4, 5, …

Так как 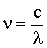, то для частот соотношение (4.2.28) примет вид:

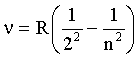(4.2.29)

где R = R'·с.

Все линии спектра, определяемые формулой (4.2.29), называются серией Бальмера. Формулы вида (4.2.29) могут быть записаны и для линий других частей спектра (серии ПашенадляИК части спектра, серией Лаймана для УФ части спектра и др.). Поэтому для всех спектральных линий водорода были предложены единые формулы:

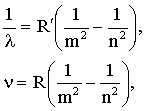(4.2.30)

где m и n - целые числа, причем для данной серии n = m + 1, m + 2, m + 3, … и т.д.

Для серии Лаймана m = 1, для серии Бальмера m = 2, для серии Пашена m = 3 и т.д.

Исторически первой моделью строения атома была планетарная классическая модель Резерфорда. Опираясь на данные экспериментальных исследований рассеяния быстрых частиц в веществе, Резерфорд пришел к выводу, что строение атома можно уподобить планетной системе, где в центре находится компактное положительно заряженное ядро, в котором сосредоточена почти вся масса атома, а по орбитам вокруг ядра вращаются электроны. Число электронов равно порядковому номеру элемента в таблице Менделеева. Силы, связывающие между собой ядро и электроны - электрической природы.

Однако модель Резерфорда несла в себе серьезные противоречия. Согласно законам классической электродинамики, электрон, вращающийся по орбите, представляет собой высокочастотный переменный ток, который порождает переменное магнитное поле. Следовательно, должна возникать электромагнитная волна, которая будет уносить энергию электрона в атоме. Такой электрон тогда должен непрерывно изменять (уменьшать) свою орбиту и в конечном счете упасть на ядро. Спектр излучения должен быть не дискретным (линейчатым), а сплошным, что на практике не наблюдается.

Поэтому Нильс Бор предложил (1913) более последовательную квантовую модель строения атома водорода. Он развил модель Резерфорда, дополнив ее рядом положений, опирающихся на опытные данные - постулатов.

Первый постулат Бора (постулат стационарных состояний): существуют стационарные состояния электронов в атоме, находясь в которых, они не излучают энергию.

Этим состояниям соответствуют стационарные электронные орбиты. Для таких орбит справедливо правило квантования Бора: в стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь квантованные (дискретные) значения момента импульса:

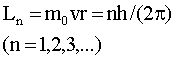(4.2.31)

где m₀ и v - масса и скорость электрона, r - радиус его орбиты.

Второй постулат (правило частот): при переходе атома из одного стационарного состояния в другое испускается или поглощается один фотон.

Излучение происходит при переходе атома из состояния с большей энергией в состояние с меньшей энергией, т.е. при переходе электрона с орбиты более удаленной от ядра на ближнюю к ядру стационарную орбиту. Поглощение фотона сопровождается переходом атома в состояние с большей энергией, в результате электрон переходит на более удаленную от ядра стационарную орбиту. Изменение энергии атома, связанное с излучением или поглощением фотона, пропорционально частоте:

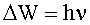(4.2.32)

Если W_m и W_n - энергия атома в двух стационарных состояниях, то формулу (4.2.32) можно представить так:

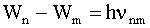(4.2.33)

В атоме водорода вокруг положительно заряженного ядра движется один электрон. Ядро, в силу его большой, по сравнению с электроном, массы, можно считать неподвижным, а орбиту электрона - круговой. Центростремительной силой, удерживающей электрон в атоме, является кулоновская сила притяжения ядра и электрона:

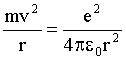(4.2.34)

Используя (4.2.31) и (4.2.34), имеем для радиуса орбиты электрона в атоме водорода:

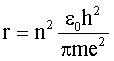(4.2.35)

Ясно, что этот радиус зависит от квантового числа n = 1, 2, 3,…. Для ближайшей к ядру орбиты (n = 1) получим r₁ = 0,53 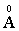. По сути, эта величина определяет размер атома водорода в основном состоянии.

Радиусы стационарных орбит относятся между собой как квадраты чисел натурального ряда: 1:4:9:16 и т.д.

Определим сейчас полную энергию электрона в атоме. Она слагается из кинетической энергии движения электрона по орбите и потенциальной энергии притяжения электрона к ядру. Используя (4.2.34), получим для кинетической энергии:

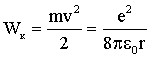(4.2.36)

Потенциальная энергия притяжения двух разноименных зарядов равна:

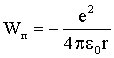(4.2.37)

Суммируя (4.2.36) и (4.2.37), получаем:

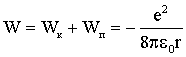(4.2.38)

Подставляя в (4.2.38) выражение для радиуса (4.2.35), имеем:

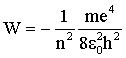(4.2.39)

Согласно этому выражению, можно рассчитать энергию электрона для любой стационарной орбиты. Для n = 1 W₁ = –13,55 эВ. Полная энергия электрона, находящегося на стационарной орбите, называется уровнем энергии атома. Минимум энергии атома - значение W₁ = –13,55 эВ, максимум энергии W = 0 - при движении электрона по столь далекой орбите (n = ∞), на которой электрон уже не связан с ядром (атом превращается в ион).

Самопроизвольный переход электрона на более далекую орбиту (более высокий энергетический уровень) невозможен. Для такого перехода атому извне необходимо сообщить определенную энергию (возбудить атом). Так, переход электрона с первой стационарной орбиты на вторую происходит при поглощении атомом кванта с энергией 10,17 эВ. Таким образом, атом может излучать или поглощать волны только вполне определенных частот, чем и обусловлен линейчатый характер спектра атома водорода.

Нормальным состоянием атома является такое, при котором электрон движется по ближайшей к ядру орбите. Атом в этом состоянии не может излучать энергию. Все остальные уровни энергии атома водорода называются возбужденными.