Повышающий и понижающий операторы

,

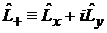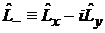. (7.9)

Действуя на сферическую функцию 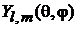, операторы 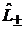изменяют на единицу число m, т. е. проекцию вектора момента импульса на ось z.

Выполняются

,

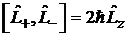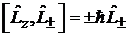, (7.11)

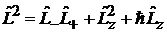. (7.12)

Доказательство (7.12):

,

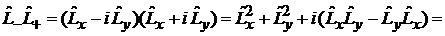
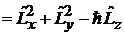где использовано

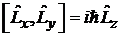. (7.8)

УРАВНЕНИЕ СферическОЙ функциИ

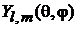является собственной функцией оператора квадрата момента импульса

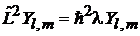, (7.13)

где 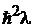– собственное значение оператора 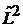. Если объект находится в состоянии 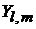, то квадрат момента импульса равен .

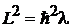С учетом

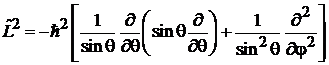, (7.5)

уравнение для сферической функции

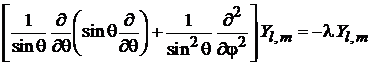. (7.14)

Ищем решение уравнения 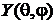и собственное значение λ.

Разделение переменных

Слагаемые (7.14) имеют производные от разных аргументов, поэтому аргументы решения разделяются

.

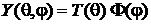Подставляем в уравнение, умноженное слева на 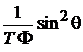, и группируем слагаемые по их аргументам

.

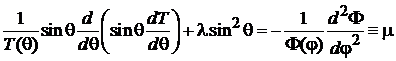Левая и правая стороны зависят от разных аргументов, поэтому они равны постоянной m. В результате получаем независимые уравнения

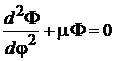, (7.15)

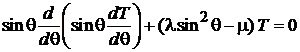. (7.16)

Решение уравнения (7.15)

1. Уравнение (7.15) является уравнением Гельмгольца и имеет решение

.

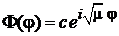2. Однозначность решения накладывает условие периодичности по углу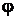

.

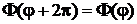Получаем

,

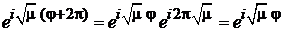откуда

, ,

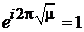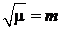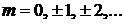– магнитное число,

.

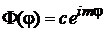3. Квадрат модуля функции состояния является плотностью вероятности состояния и удовлетворяет условию нормировки

,

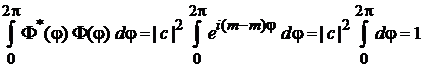тогда

,

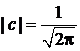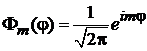. (7.17)

На основании

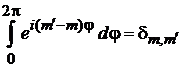(1.43)

выполняется условие ортонормированности

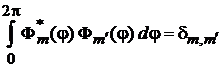. (7.18)

4. Для оператора проекции момента импульса

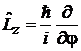, (7.4)

выполняется

,

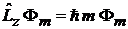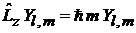. (7.19)

Следовательно, 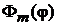и 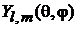– собственные функции оператора проекции момента импульса на ось z с собственным значением 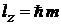. В состоянии, описываемом функцией 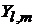, измерение проекции момента импульса на ось z дает

.

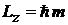Значение l в уравнении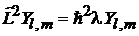

1. Оператором

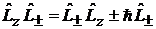(7.11)

действуем на 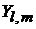и используем

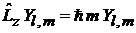, (7.19)

получаем

.

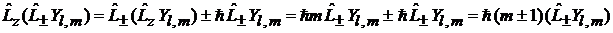Операторы 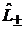переводят состояние с собственным значением m в состояния с собственными значениями 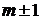, т. е. 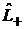– повышающий оператор, 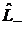– понижающий оператор.

2. Проекция вектора не превышает его модуль. Если

,

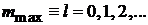то нет состояний с 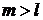, тогда действие повышающего оператора на состояние с максимальной проекцией

.

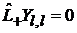3. Действуем на 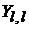оператором

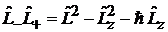. (7.12)

Используем

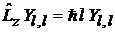(7.19)

и

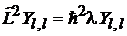, (7.13)

тогда

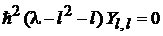
и находим

.

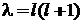4. В результате

,

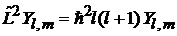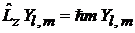, (7.20)

где

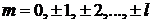– магнитное число;

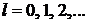– орбитальное число;

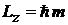– проекция орбитального момента на ось z;

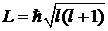– модуль орбитального момента.

Пространственное квантование орбитального момента

При l = 3 получаем

,

,

.

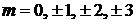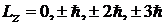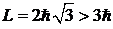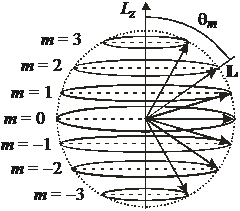
Угол ориентации L квантуется

, ;

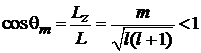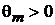число возможных проекций равно ;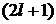

Вектор момента импульса L не может быть направлен вдоль Оz.

Решение уравнения (7.16)

С учетом 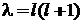уравнение

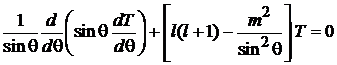(7.16)

совпадает с уравнением (6.116) для присоединенной функции Лежандра, тогда

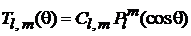. (7.21)

С учетом

,

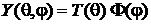получаем

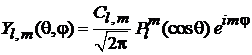. (7.22)

Накладываем условие нормировки

,

.

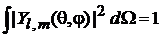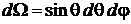Учитываем

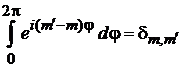, (1.43)

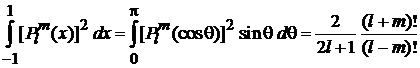, (6.123)

получаем

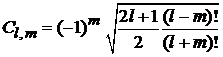. (7.23)

Сферическая функция

В результате

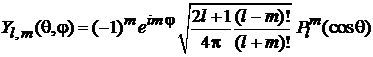, (7.24)

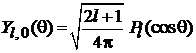. (7.24а)

Из

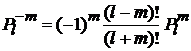(6.120)

следует соотношение между состояниями с противоположными проекциями

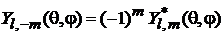. (7.25)

Используем

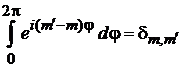, (1.43)

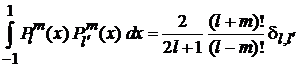, (6.123)

получаем условие ортонормированности

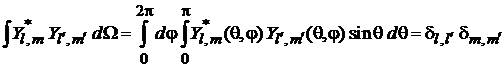. (7.27)

Инверсия координат

Заменяем

,

,

,

, ,

,

,

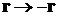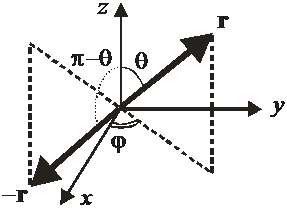
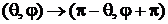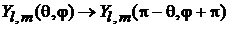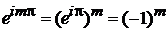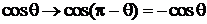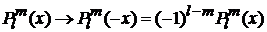получаем

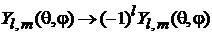. (7.28)

Четность состояния, описываемого сферической функцией, совпадает с четностью орбитального числа l.

Частные выражения

Используем

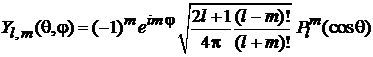, (7.24)

и находим

,

,

,

,

,

,

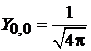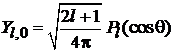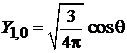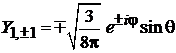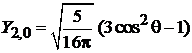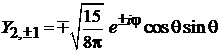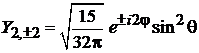. (7.29)

При 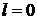нет зависимости от углов – центрально-симметричное распределение;

При 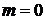нет зависимости от угла φ – осесимметричное распределение.

Плотность вероятности