Полиномиальное представление

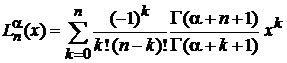, (6.44)

где n – высшая степень полинома .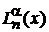

Доказательство (6.44):

Дифференцирование в (6.42) проводим по формуле Лейбница

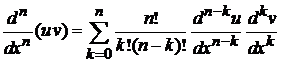. (6.45)

Например, при 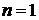получаем известную формулу

.

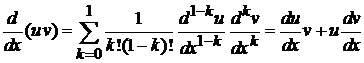В (6.45) полагаем 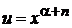, 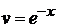и учитываем

.

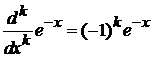Соотношение

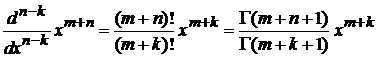
обобщаем на случай 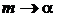– не целое

.

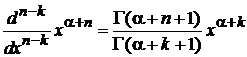В результате

.

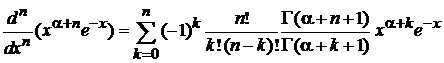Подставляем в

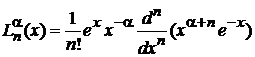, (6.42)

получаем полином порядка n

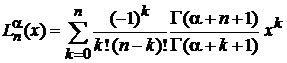. (6.44)

Из (6.44)

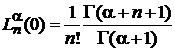. (6.47)

Полиномы низших степеней

Из (6.42) и (6.44) получаем:

,

,

,

.

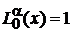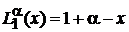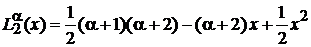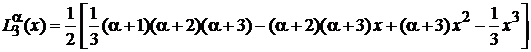При :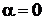

,

,

,

.

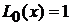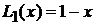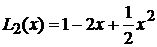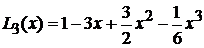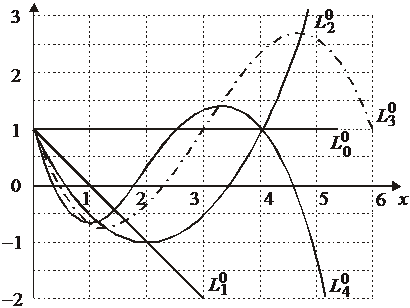
Производящая функция

Методом факторизации ранее получено

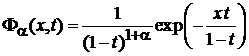. (6.52)

По определению

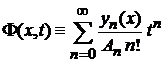(5.14)

с учетом 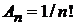получаем

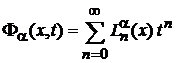. (6.53)

Рекуррентные соотношения

1. Дифференцируем по x (6.52)

.

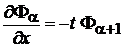Подставляем (6.53)

.

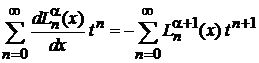Приравниваем коэффициенты при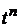

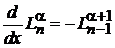. (6.54)

Дифференцируя далее (6.54), получаем

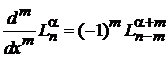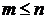, . (6.55)

В (6.55) при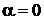

,

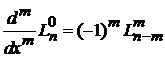заменяем 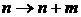и получаем выражение обобщенного полинома Лагерра через полином Лагерра

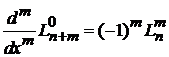. (6.56)

3. Из уравнения Лагерра

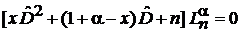, (6.41)

используя

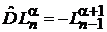, (6.54)

,

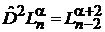получаем

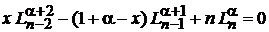. (6.57)

4. Выражение

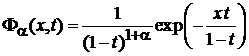, (6.52)

дифференцируем по t

.

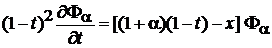Подставляем

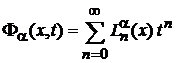, (6.53)

получаем

.

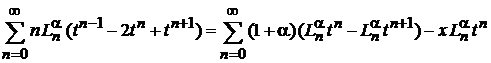Приравниваем коэффициенты при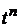

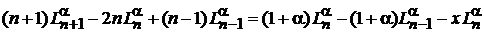
находим

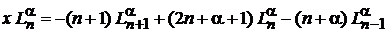. (6.58)

5. Из

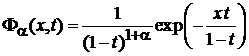(6.52)

Следует

.

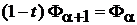Подставляем

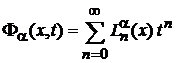, (6.53)

получаем

.

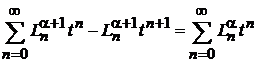Приравниваем коэффициенты при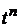

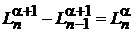. (6.59)

Из (6.58) в виде

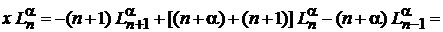
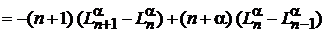
С учетом (6.59)

,

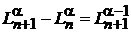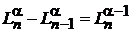
Получаем

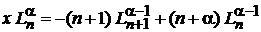. (6.60)

Заменяем 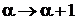и

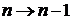
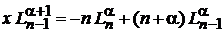. (6.61)

Из (6.58) в виде

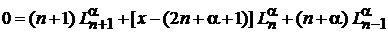
вычитаем (6.61) и получаем

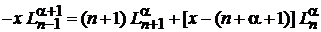. (6.64)

Условие ортонормированности

Методом факторизации ранее получено (П.3.11). Доопределяем 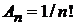и получаем

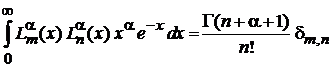. (6.67)

Разложение функции по ортонормированному базису

Функцию 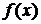, определенную при 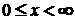, разлагаем по базису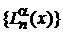

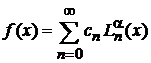. (6.68)

Находим коэффициенты разложения. Умножаем (6.68) на 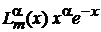, интегрируем, учитываем (6.67). В сумме остается лишь одно слагаемое за счет символа Кронекера. После замены 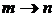получаем

.

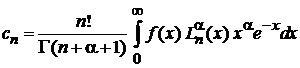Подставляем

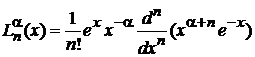, (6.42)

интегрируем по частям n раз, находим коэффициент

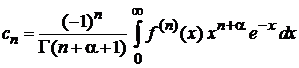. (6.69)

Интегралы с полиномами Лагерра

1. Вычисляем

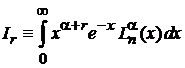, r – целое.

Подставляем

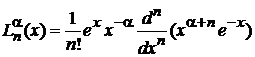(6.42)

тогда

.

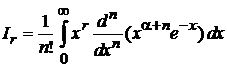Интегрируем по частям n раз

,

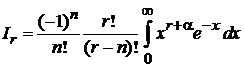где учтено

.

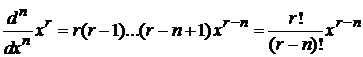Используем определение гамма-функции

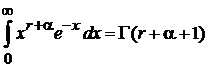, (4.1)

находим

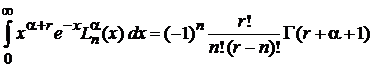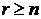, , (6.70)

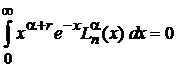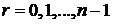, . (6.71)

Из (6.70) пр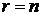и и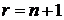

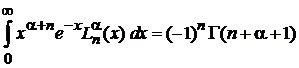, (6.72)

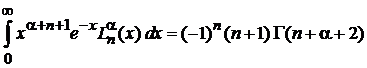. (6.73)

2. Вычисляем

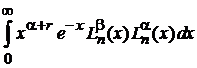, r – целое.

Подставляем

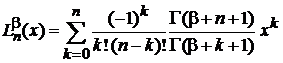. (6.44)

Интегралы сводятся к

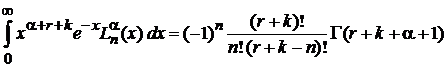, (6.70)

тогда

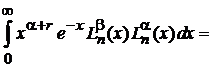
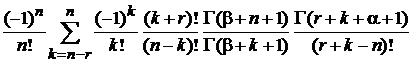= . (6.74)

При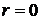

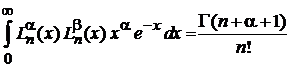, (6.75)

что дает условие нормировки (6.67).

При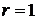

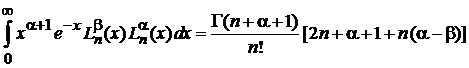. (6.76)

3. Вычисляем интеграл, отличающийся от (6.70) знаком перед r:

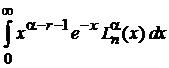, r – целое, .

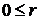В формуле

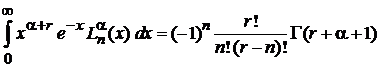(6.70)

заменяем 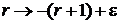, где :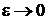

,

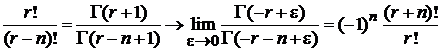где использовано

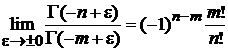. (4.4)

Тогда из (6.70) после указанной замены

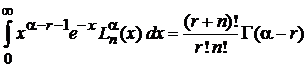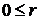, . (6.77)

Пр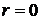и и 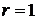из (6.77) получаем

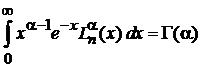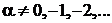, , (6.79)

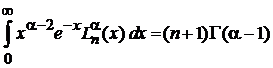. (6.80)

4. Вычисляем

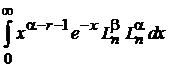, r – целое.

Для 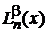используем

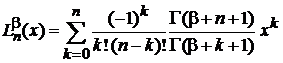. (6.44)

Интегралы сводятся к (6.77) в виде

,

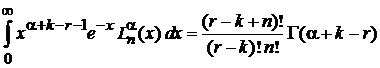тогда

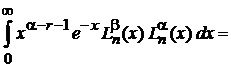
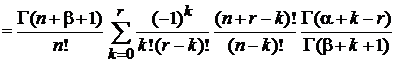. (6.81)

Пр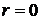и и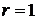

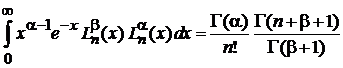, (6.82)

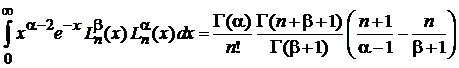. (6.83)

Связанные состояния электрона в АтомЕ водорода

Характеристики атома протия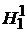

1. Тяжелый протон с зарядом +е. Легкий электрон с массой μ и с зарядом –е. Движение электрона описываем в сферических координатах, в центре – протон.

2. Потенциальная энергия электрона в СГС

, .

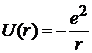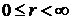3. Кинетическая энергия радиального движения

,

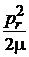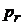– радиальный импульс.

4. Кинетическая энергия углового движения

,

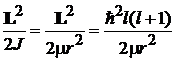L – орбитальный момент;

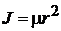– момент инерции электрона;

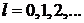– орбитальное квантовое число.

5. Полная энергия электрона

.

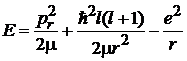Для связанного состояния .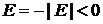

6. Выражаем квадрат радиального импульса

.

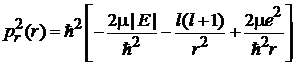Уравнение Шредингера для радиальной части волновой функции 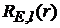электрона

.

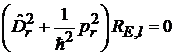В сферических координатах

,

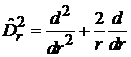тогда

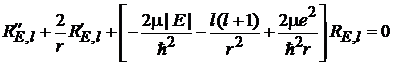. (6.84)

Упрощаем уравнение

Вводим боровский радиус

.

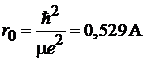Заменяем 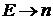– безразмерная величина:

,

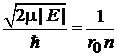тогда

.

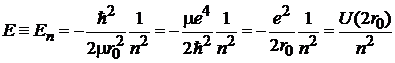Будет доказано, что n квантуется – 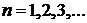, тогда получаем дискретный спектр

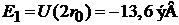– основное состояние,

,

.

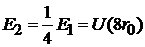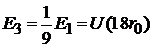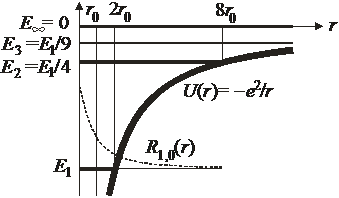
Исходное уравнение

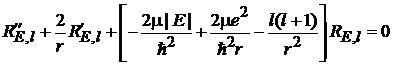(6.84)

получает вид

, .

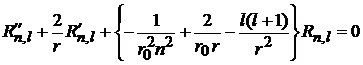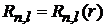Переходим к безразмерной x

, , , .

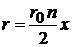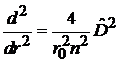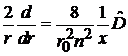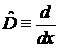Уравнение умножаем на 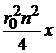и получаем

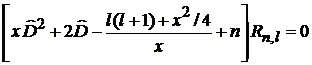, (6.85)

, .
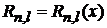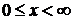