Рекуррентные соотношения для полиномов

Алгоритм получения:

1. Дифференцируем (6.10) по одному из аргументов.

2. В полученное соотношение подставляем (6.11).

3. Приравниваем слагаемые с одинаковыми степенями t.

Соотношение 1 для полинома Эрмита

Из

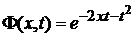(6.10)

получаем

.

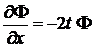Подставляем (6.11)

,

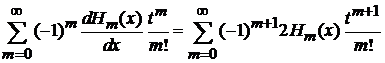приравниваем слагаемые с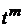

,

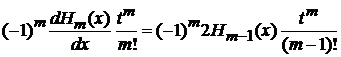получаем

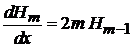, (6.12)

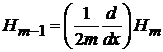. (6.13)

Соотношение 2

Из

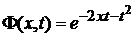(6.10)

получаем

.

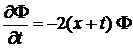Подставляем

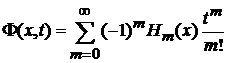, (6.11)

находим

,

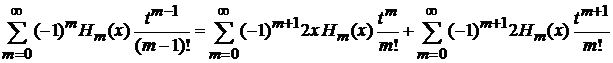приравниваем слагаемые с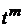

,

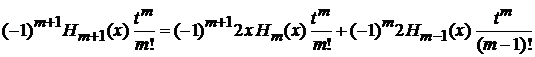Получаем

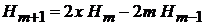. (6.15)

Учет

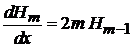(6.12)

дает

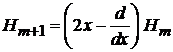. (6.16)

Условие ортонормированности

Множество 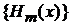образует базис в гильбертовом пространстве функций, определенных при 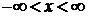, сусловием ортонормированности (П.3.4)

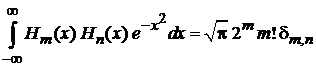. (6.18)

Разложение функции по полиномам Эрмита

Если 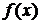определена при 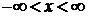, то она разлагается по базису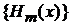

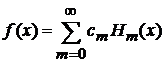. (6.19)

Находим коэффициент :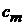

· умножаем (6.19) на ,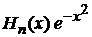

· интегрируем по интервалу ,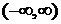

· меняем порядок суммирования и интегрирования,

· учитываем ортонормированность (6.18),

· символ Кронекера снимает сумму, оставляя одно слагаемое:

.

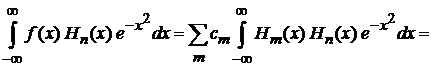
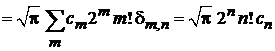Заменяем 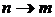и получаем

.

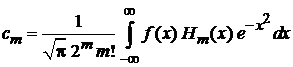· Подставляем полином в форме Родрига

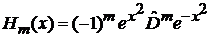, (6.2)

получаем

.

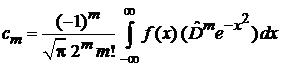Интегрируем по частям m раз, свободные слагаемые зануляются на обоих пределах, получаем коэффициент

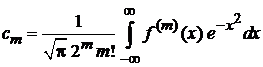. (6.20)

Интегралы с полиномами Эрмита

1. Вычисляем

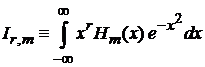
Учитываем четность

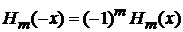. (6.3)

Если 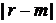– нечетное, тогда

.

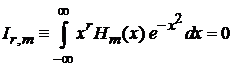Если 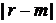– четное, то в 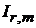подставляем форму Родрига

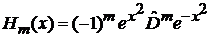. (6.2)

Интегрируем по частям m раз, свободные слагаемые зануляются

= .

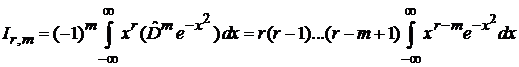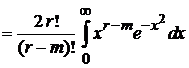Используем

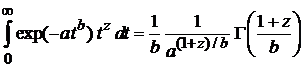(4.9)

при 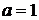, , 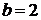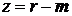и находим

.

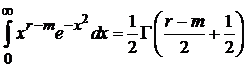Учитываем

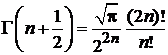, (4.11)

тогда

.

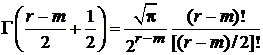В результате

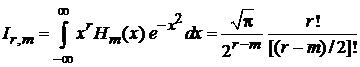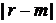, – четное. (6.21)

Из (6.21) при 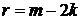с учетом 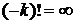получаем

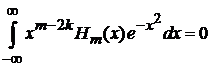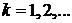, (6.21а)

Из (6.21) при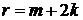

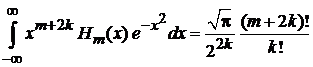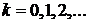, (6.22)

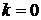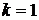Из (6.22) при и находим

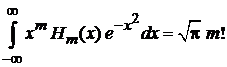, (6.23)

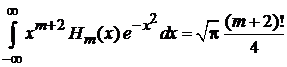. (6.24)

В формуле

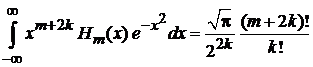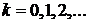, (6.22)

заменяем 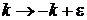, где 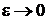. Преобразуем правую сторону (6.22)

.

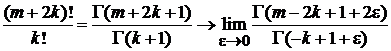Используем (4.4) в виде

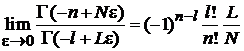
при 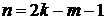, , 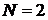, , 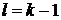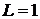в результате

.

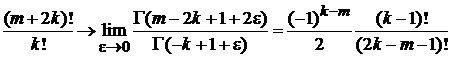В результате (6.22)

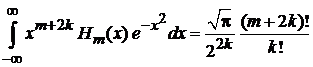
при 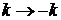дает

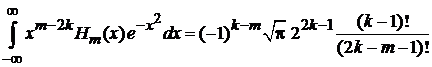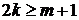, . (6.25)

Из (6.25) пр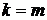и и 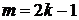получаем

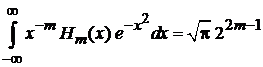, (6.26)

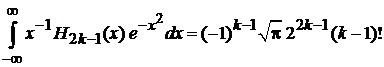. (6.27)

2. Вычисляем

,

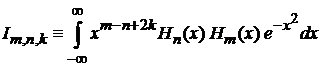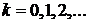
Для 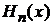используем полиномиальную форму

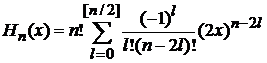, (6.4)

тогда

.

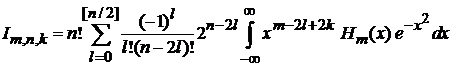Используем

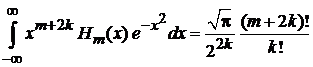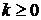, , (6.22)

при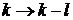

.

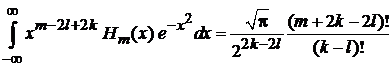В результате

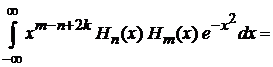
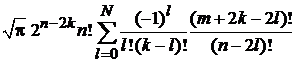= , (6.28)

где знаменатели с факториалами ограничивают .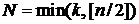

При 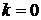, 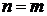из (6.28) получаем нормировку полиномов Эрмита

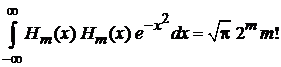. (6.29)

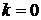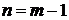При , и при 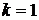, 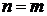находим

,

.

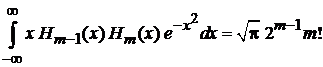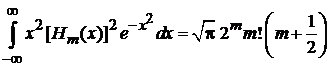Гармонический осциллятор

Система, колеблющаяся по гармоническому закону. От лат. oscillatio – «качание».

Осциллятор в классической теории

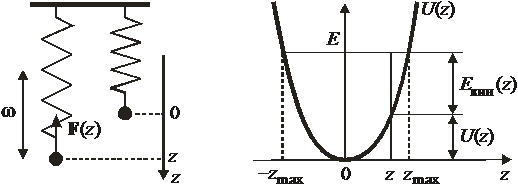
Масса µ находится в поле упругой потенциальной энергии

.

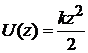Упругая сила

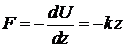
создает ускорение 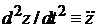. Второй закон Ньютона

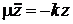
дает уравнение Гельмгольца

,

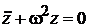где частота колебаний

, ,

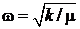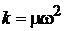тогда

.

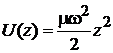Решение уравнения дает колебания

,

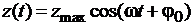где – амплитуда.

Полная энергия

.

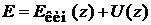При максимальном смещении

,

тогда

.

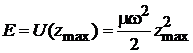Полная энергия зависит от амплитуды колебаний , и может быть любой. Квадрат импульса

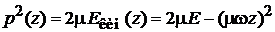(6.30)

Осциллятор в квантовой теории

В квантовой теории спектр энергии эквидистантный

, ,

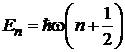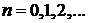уровню n сопоставляются n квантов энергии ;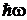

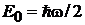– энергия вакуума.

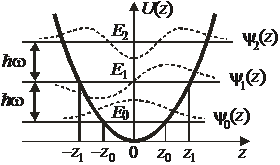
Уравнение Шредингера

.

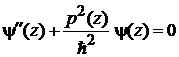Для осциллятора учитываем

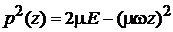, (6.30)

получаем для состояния 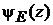уравнение

.

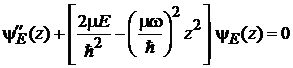Переходим к безразмерной координате

, ,

, ,

,

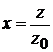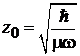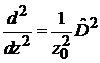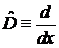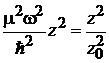Для

,

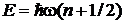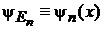
с учетом

,

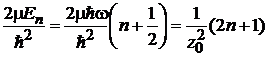получаем уравнение

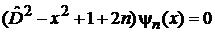, (6.31)

Методом факторизации ранее получено решение (П.3.6) в виде функции Эрмита

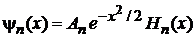. (6.32)

Из (6.3)

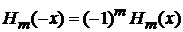и (6.32) находим

.

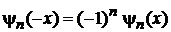Условие ортонормированности

Из (П.3.7)

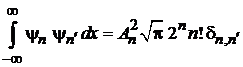при

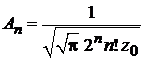
получаем

,

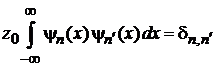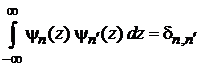. (6.33)

Учитывая 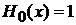, , 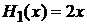, 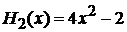из (6.32) находим основное состояние

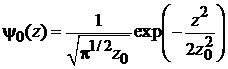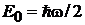, (6.33а)

и первое возбужденное состояние

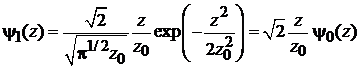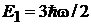, . (6.33б)

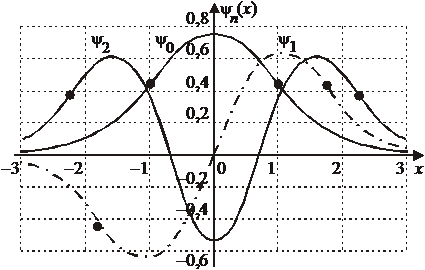
Точки поворота классического осциллятора

, , , .

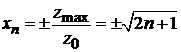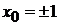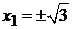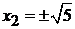Рекуррентные соотношения

· Умножаем (6.15)

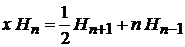на 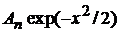и учитываем

, , ,

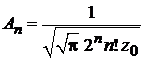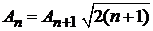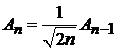для

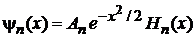. (6.32)

находим

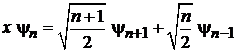. (6.34)

· Дифференцируем

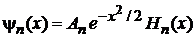, (6.32)

.

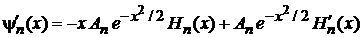Учитываем (6.12)

, ,

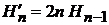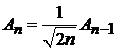Получаем

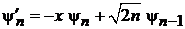. (6.35)

Из (6.35)

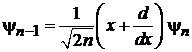. (6.36)

· Из

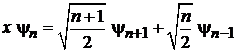(6.34)

выражаем

.

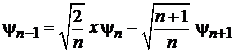Подстановка в (6.35) дает

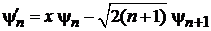. (6.37)

Из (6.37) находим

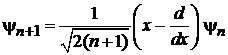. (6.38)

· Суммирование (6.35) и (6.37) дает

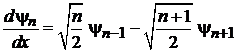. (6.39)

Лестничные операторы

Изменяют состояние n на единицу

,

.

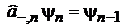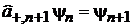Из (6.36) и (6.38) получаем

,

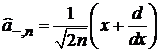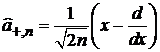. (6.40)

Матричный элемент

Вероятность перехода системы между состояниями 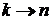под действие оператора 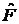выражается матричным элементом 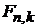. По индексам переход происходит справа налево.

Математический смысл

В гильбертовом пространстве с базисом 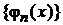и весовой функцией 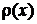матричный элемент оператора 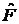между ортам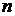и и 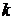определяется в виде скалярного произведения

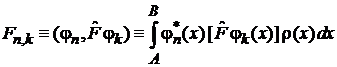, (1)

где A, B, 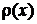– вещественные.

Физический смысл

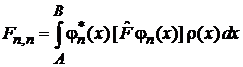
– диагональный матричный элемент есть среднее значение величины f, описываемой оператором 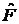, в состоянии .

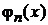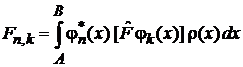
– недиагональный матричный элемент 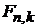есть амплитуда вероятности переходамежду состояниями 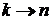под действием оператора .

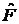Вероятность перехода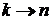

.
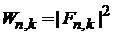