Признаки сходимости интегралов 2-го рода.
Для определенности будем рассматривать несобственные интегралы 2-го рода вида 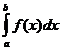 =
=  .Установленные ниже утверждения легко переносятся на несобственные интегралы 2-го рода вида
.Установленные ниже утверждения легко переносятся на несобственные интегралы 2-го рода вида 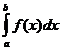 =
=  и
и 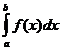 =
=  +
+  .
.
Теорема 1.Пусть с – любое число, удовлетворяющее условию a<c<b. Тогда несобственные интегралы 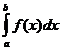 и
и  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Доказательство. Возьмем произвольное число b, удовлетворяющее условию с<b<b. Имеем  =
= +
+ (4)
(4)
1) Пусть  сходится Þ существует конечный предел
сходится Þ существует конечный предел  . Но тогда из (4) Þ, что существует конечный предел
. Но тогда из (4) Þ, что существует конечный предел  Þ
Þ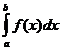 сходится.
сходится.
2) Пусть 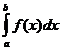 сходится Þ существует конечный предел
сходится Þ существует конечный предел  . Но тогда из (4) Þ, что существует конечный предел
. Но тогда из (4) Þ, что существует конечный предел  Þ
Þ сходится.
сходится.
В случаях 1) и 2) будем имеем: 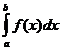 =
= +
+ .
.
3) Пусть 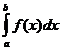 расходится. Покажем, что и
расходится. Покажем, что и  расходится.
расходится.
Допустим, что  сходится. Тогда по пункту 1) должен сходится и
сходится. Тогда по пункту 1) должен сходится и 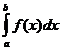 . Получили противоречие.
. Получили противоречие.
4) Пусть  расходится. Покажем, что и
расходится. Покажем, что и 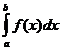 расходится.
расходится.
Допустим, что 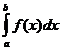 сходится. Тогда по пункту 1) должен сходится и
сходится. Тогда по пункту 1) должен сходится и  . Получили противоречие. Ч.т.д.
. Получили противоречие. Ч.т.д.
Теорема 2. Если f(x)³0 хотя бы для xÎ[с;b) (а£с<b), то для сходимости интеграла  (а значит и интеграла
(а значит и интеграла 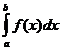 ) необходимо и достаточно, чтобы существовало число K>0 такое, что
) необходимо и достаточно, чтобы существовало число K>0 такое, что  £К, для любого bÎ(с;b).
£К, для любого bÎ(с;b).
Доказательство. Интеграл  =j(b), т.е. представляет собой функцию от b, возрастающую с увеличением b. Для существованию конечного предела у функции j(b) при b®b-0 необходимо и достаточно, чтобы она была ограничена сверху, т.е. чтобы существовало число K>0 такое, чтобы j(b)=
=j(b), т.е. представляет собой функцию от b, возрастающую с увеличением b. Для существованию конечного предела у функции j(b) при b®b-0 необходимо и достаточно, чтобы она была ограничена сверху, т.е. чтобы существовало число K>0 такое, чтобы j(b)=  £К, для любого bÎ(с;b). Ч.т.д.
£К, для любого bÎ(с;b). Ч.т.д.
Теорема 3 (1-й признак сравнения несобственных интегралов).
Пусть хотя бы для хÎ[с;b) (а£с<b) функции f(x) и g(x) удовлетворяют условию 0≤f(x)≤g(x). Тогда:
1) из сходимости интеграла  (5) следует сходимость интеграла
(5) следует сходимость интеграла 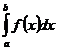 (6)
(6)
2) из расходимости интеграла 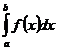 следует сходимость интеграла
следует сходимость интеграла  .
.
Доказательство. Возьмем произвольное число b, такое, что с<b<b
Тогда 0£  £
£  (7).
(7).
1) Пусть  сходитсяÞ
сходитсяÞ  сходитсяÞ существует число K>0 такое, что
сходитсяÞ существует число K>0 такое, что  £К "bÎ(с;b). Но тогда из (7) следует, что
£К "bÎ(с;b). Но тогда из (7) следует, что  £К "bÎ(с;b). Þпо теореме 2:
£К "bÎ(с;b). Þпо теореме 2:  - сходитсяÞ
- сходитсяÞ 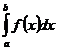 - сходится.
- сходится.
2) Пусть 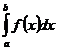 - расходится. Нужно доказать, что расходится и
- расходится. Нужно доказать, что расходится и  . Допустим противное, что
. Допустим противное, что  сходится. Тогда по пункту 1) должен сходится и
сходится. Тогда по пункту 1) должен сходится и 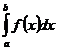 . Получили противоречие. Ч.т.д.
. Получили противоречие. Ч.т.д.
Теорема 4. (б.д.) (2-й признак сравнения).Пусть f(x)>0 и g(x)>0 хотя бы для хÎ[с;b) (а£с<b). Пусть существует конечный, отличный от нуля предел
l=  (l¹0, l¹¥).
(l¹0, l¹¥).
Тогда интегралы 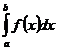 и
и  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Для применения теорем 3 и 4 требуется знание некоторой «эталонной» функции g(x). Часто в этой роли выступает функция g(x)=  (р>0, xÎ[a,b), a<b).
(р>0, xÎ[a,b), a<b).
Пример. Исследуем на сходимость интеграл  .
.
1) Пусть р<1. Тогда
 =
=  =
=  Þ
Þ  =
=  Þ
Þ
Þ  сходится при р<1.
сходится при р<1.
2) Пусть р=1. Тогда  =
=  =ln(b-a)-ln(b-b)Þ
=ln(b-a)-ln(b-b)Þ  =+¥Þ
=+¥Þ
Þ  расходится при р=1.
расходится при р=1.
3) Пусть р>1. Тогда
 =
=  =
=  Þ
Þ  =+¥Þ
=+¥Þ
Þ  расходится при р>1.
расходится при р>1.
Пример.Исследовать на сходимость интеграл I=  .
.
Подынтегральная функция разрывна в точке х=0.
 <
<  , здесь р=
, здесь р=  <1, следовательно
<1, следовательно  сходится. Значит сходится и интеграл от меньшей функции, т.е.
сходится. Значит сходится и интеграл от меньшей функции, т.е.  .
.
Пример. Исследовать на сходимость интеграл I=  .
.
f(x)=  определена в промежутке [0,1] всюду, за исключением точек х=0 и х=1. (эти точки – особые). Представим I в виде суммы двух интегралов:
определена в промежутке [0,1] всюду, за исключением точек х=0 и х=1. (эти точки – особые). Представим I в виде суммы двух интегралов:
I=  +
+  =I1+I2.
=I1+I2.
Рассмотрим I1=  . У этого интеграла 1 особая точка х=0. Имеем
. У этого интеграла 1 особая точка х=0. Имеем
 =
=  = - ¥Þ f(x) неограниченная в правой полуокрестности точки х=0. Значит I1 – несобственный интеграл 2-го рода.
= - ¥Þ f(x) неограниченная в правой полуокрестности точки х=0. Значит I1 – несобственный интеграл 2-го рода.
Т.к. f(x)=  ~ln x при х®+0, то в качестве функции g(x) возьмем g(x)=ln x. Тогда
~ln x при х®+0, то в качестве функции g(x) возьмем g(x)=ln x. Тогда  =
=  =
=  =1.
=1.
Следовательно, несобственные интегралы  и
и  в смысле сходимости ведут себя одинаково.
в смысле сходимости ведут себя одинаково.
 =
=  =
=  =
=  =
=
=  -
-  =
=  -0=
-0=  .
.
Т.о.  сходится. Значит и I1 сходится.
сходится. Значит и I1 сходится.
Рассмотрим I2=  . У этого интеграла 1 особая точка х=1. Имеем
. У этого интеграла 1 особая точка х=1. Имеем
 =
=  =
=  =
=  =
=  Þ f(x) ограниченная в промежутке
Þ f(x) ограниченная в промежутке  . Положим
. Положим

Функция  ограничена на
ограничена на  Þ
Þ  существует. Следовательно, I2=
существует. Следовательно, I2=  сходится.
сходится.
Т.к. несобственные интегралы I1 и I2 сходятся, то сходится и интеграл I=  .
.
