Вычисление двойного интеграла
Предположим, что область  можно задать в виде системы неравенств:
можно задать в виде системы неравенств:
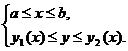
Геометрически это означает, что каждая вертикальная прямая 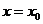
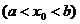 пересекает границу области
пересекает границу области  только в двух точках М1 и М2 (рис. 3), которые называются соответственно точкой входа и точкой выхода.
только в двух точках М1 и М2 (рис. 3), которые называются соответственно точкой входа и точкой выхода.
Тогда
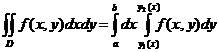 .
.
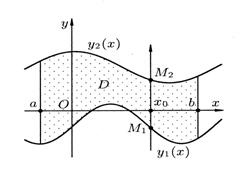 Рис. 3. Рис. 3. | 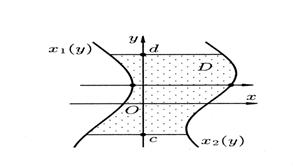 Рис. 4. Рис. 4. |
Если же область  (рис.4) можно задать в виде системы неравенств:
(рис.4) можно задать в виде системы неравенств:
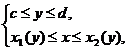
то
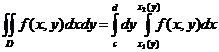 .
.
Интегралы. стоящие в правых частях приведенных равенств, называются повторными. Они отличаются друг от друга порядком интегрирования. Интеграл, содержащий функцию 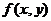 , называется внутренним, другой – внешним. При вычислении повторных интегралов следует брать сначала внутренний интеграл, при этом переменная, не стоящая под знаком дифференциала, принимается постоянной. Затем вычисляется внешний интеграл. Каждый из них вычисляется при помощи формулы Ньютона – Лейбница, как определенный интеграл.
, называется внутренним, другой – внешним. При вычислении повторных интегралов следует брать сначала внутренний интеграл, при этом переменная, не стоящая под знаком дифференциала, принимается постоянной. Затем вычисляется внешний интеграл. Каждый из них вычисляется при помощи формулы Ньютона – Лейбница, как определенный интеграл.
Области, не представимые в описанном выше виде, следует разбить на конечное число таких областей при помощи прямых, параллельных координатным осям (рис. 5). При вычислении двойных интегралов по таким областям следует применить свойство аддитивности.
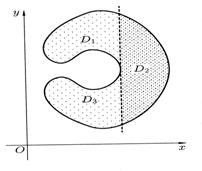
Рис. 5.
Пример 1.Вычислить повторный интеграл 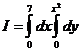 .
.
Сначала вычислим внутренний интеграл по формуле Ньютона – Лейбница. Его результат будет подынтегральной функцией для внешнего интеграла.
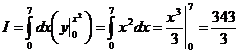 .
.
Пример 2.Вычислить повторный интеграл 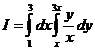 .
.
Множитель  (он не зависит от
(он не зависит от 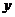 , поэтому может считаться постоянным для внутреннего интеграла) можно вынести за знак интеграла, т. е. перенести во внешний интеграл:
, поэтому может считаться постоянным для внутреннего интеграла) можно вынести за знак интеграла, т. е. перенести во внешний интеграл:
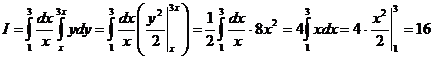 .
.
Пример 3.Вычислить двойной интеграл 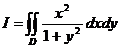 , где
, где  - прямоугольник
- прямоугольник 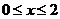 ,
, 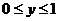 .
.
Преобразуем двойной интеграл в повторный. Пределы интегрирования известны, поэтому
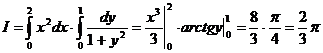 .
.
Повторный интеграл свелся к произведению двух независимых друг от друга интегралов, поскольку результат вычисления внутреннего интеграла есть число.
Пример 4. Вычислить интеграл 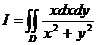 , где область
, где область  - параболический сегмент, ограниченный параболой
- параболический сегмент, ограниченный параболой 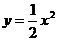 и прямой
и прямой 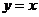 .
.
Изобразим область интегрирования  (рис.6). Так как прямая
(рис.6). Так как прямая 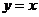 и парабола
и парабола
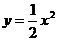 пересекаются в точках
пересекаются в точках 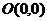 и
и 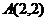 , то область
, то область  определяется системой неравенств
определяется системой неравенств 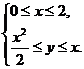
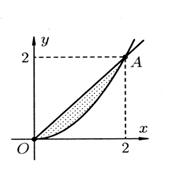
Рис. 6.
Теперь вычислим искомый интеграл 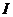 :
:
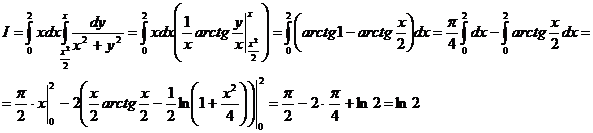
Пример 5.Вычислить интегральное среднее значение функции 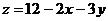 в области
в области  , ограниченной прямыми
, ограниченной прямыми 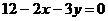 ,
, 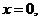
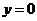 .
.
Область  - треугольник ОАВ, где
- треугольник ОАВ, где 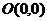 ,
, 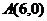 ,
, 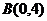 - рис. 7.
- рис. 7.
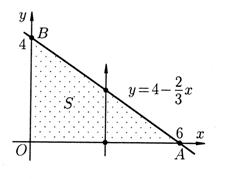
Рис. 7.
По определению интегральное среднее значение функции 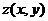 в области
в области  равно
равно 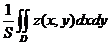 , где S – площадь области
, где S – площадь области  (свойство 3).
(свойство 3).
Площадь S вычисляется по формуле площади прямоугольного треугольника: 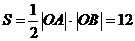 . Остается вычислить интеграл по области
. Остается вычислить интеграл по области  , которую можно задать неравенствами
, которую можно задать неравенствами 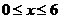 ,
, 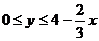 .Имеем
.Имеем
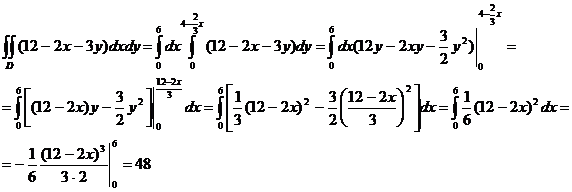
Таким образом, искомое интегральное среднее равно 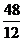 , т. е. 4.
, т. е. 4.
Контрольные вопросы:
- Дайте определение интегральной суммы для функции
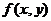 в области D.
в области D. - Что называется двойным интегралом от функции
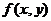 по области D?
по области D? - В чем заключается геометрический смысл двойного интеграла?
- Дайте определение интегрального среднего значения функции
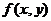 в области D?
в области D? - Что называют повторными интегралами от функции
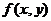 по области D?
по области D?
