Свойства двойного интеграла.
1. Двойной интеграл суммы равен сумме двойных интегралов.
2.Постоянный множитель можно вынести за знак двойного интеграла.
3.Если область (D) разбита на две области (D1) и (D2) без общих внутренних
точек, то
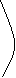

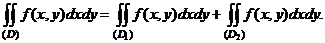
 | |||
 |
(D1) (D2)
П р и м е р . Свести двойной интеграл 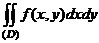 к двукратному.
к двукратному.




 (D): x = 2, y = x, xy = 1.
(D): x = 2, y = x, xy = 1.



 y
y

 y = x 2
y = x 2
y = 1/x x = y


 y x = 2
y x = 2

 1 x 2
1 x 2  x 1
x 1




 y x = 2
y x = 2
 | |||
 | |||
0.5 2 x
x = 1/y
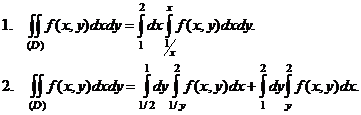
Вычисление объемов и площадей с помощью двойного интеграла.
-

 f(x,y) > 0
f(x,y) > 0
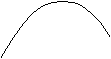
 z z = f(x,y)
z z = f(x,y)
 |

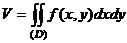
 y П р и м е р . Вычислить объем, ограниченный
y П р и м е р . Вычислить объем, ограниченный
 поверхностями: y = 9 – x2, x + z = 2, x = 0, y = 0,
поверхностями: y = 9 – x2, x + z = 2, x = 0, y = 0,
x (D) z = 0 (x ≥ 0).





 z z = 2 - x y
z z = 2 - x y
 y = 9 – x2
y = 9 – x2
 9
9
 | |||
 | |||

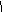
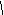 9 y
9 y
 2 0 x 2 x
2 0 x 2 x
x
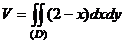
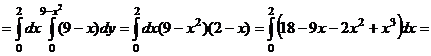
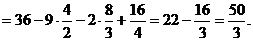
- Пусть требуется вычислить площадь области (В). Рассмотрим цилиндр, основание которого совпадает с областью (D), а высота равна единице.
 |
z V = SD ∙ h = SD.
z = 1
 |
y
 |
x (D)
С другой стороны, 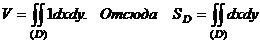 .
.
П р и м е р .Вычислить площадь, ограниченную линиями: y2 = x + 1, x – y – 1 = 0.
x = y2 – 1, y2 – y – 2 = 0, y1 = -1, y2 = 2.
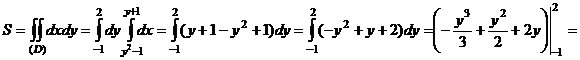
= -8/3 + 2 + 4 – 1/3 – ½ + 2 = 8 – 3 -1/2 = 9/2
 y
y

 2
2
 x = y2-1 x = y +1
x = y2-1 x = y +1
 |
-1
 x
x
 -1
-1
Двойной интеграл в полярных координатах.
 M(ρ, φ) – полярные координаты точки М.
M(ρ, φ) – полярные координаты точки М.
● M(ρ,φ) ρ – полярный радиус, φ – полярный угол.
 ρ
ρ



 φ
φ
Формулы связи между декартовыми и полярными координатами имеют вид:


 y
y
:
ρ y x = ρ cos φ, y = ρ sin φ

 φ
φ
 0 x x
0 x x




 y
y

x = ρ cosφ, y = ρ sin φ, dS = dxdy = ρdρdφ
 |
 dφ dρ
dφ dρ
x
ρ ρ + dρ
ρdφ
Двойной интеграл в полярных координатах имеет вид:

П р и м е р 1 .
Найти объем, ограниченный поверхностями: x2 + y2 = 1, z = x2 + y2, z = 0.

ρ = 1


 z
z 
 φ
φ 
 | |||
 | |||
 z = x2 + y2
z = x2 + y2  φ ρ
φ ρ
 |
y
x

П р и м е р 2. Найти объем, ограниченный поверхностями z = x2 + y2, x2 + y2 – 2y = 0, z = 0.
z




 (D)
(D)



 ρ = 2sin φ
ρ = 2sin φ

 z = x2 + y2
z = x2 + y2



 φ
φ



 y
y
0 ρ
x

Тройной интеграл.
Рассмотрим функцию u = f(x,y,z), в замкнутой области (V) трехмерного пространства.i





 P(x, y, z) Рассмотрим задачу об определении массы тела (V) при
P(x, y, z) Рассмотрим задачу об определении массы тела (V) при
условии, что плотность распределения вещества не является
постоянной величиной. Рассмотрим частичный объем ∆V c
массой ∆m.
∆m/∆V – средняя плотность.
(V)  - плотность в точке P(x, y, z).
- плотность в точке P(x, y, z).





 Pi(ξi, ηi, ςi ) Разобьем объем (V) произвольным образом на частичные
Pi(ξi, ηi, ςi ) Разобьем объем (V) произвольным образом на частичные
объемы ∆Vi. В каждом частичном объеме ∆Vi возьмем
точку Pi(ξi, ηi, ςi ) и найдем f(Pi)∙∆Vi. Это произведение
равно массе ячейки ∆Vi при условии, что плотность
постоянна и равна плотности в точке Pi.
(V)
Составим сумму  Эта сумма называется интегральной суммой.
Эта сумма называется интегральной суммой.
За массу следует принять предел при условии, что все ячейки сжимаются в точки.
(*)  .
.
λ – наибольшая из хорд, стягивающих границы ячеек.
Предел (*), если он существует, если он не зависит от способа разбиения области (V) на частичные области и от выбора точек Pi, называется тройным интегралом от функции f(x, y, z) .
Очевидно, масса тела равна
 .
.
Теорема существования.
Если функция определена и непрерывна в замкнутой области (V), то существует тройной интеграл от этой функции по области (V).
 Вычисление тройного интеграла.
Вычисление тройного интеграла.



 zz = φ2(x, y) Пусть область (V) такова, что любая
zz = φ2(x, y) Пусть область (V) такова, что любая
прямая, параллельная оси z и
проходящая через внутреннюю точку
 области (V), пересекает границу
области (V), пересекает границу
z = φ1(x, y) области ровно в двух точках.

 Y Тогда
Y Тогда
 P(x,y)
P(x,y)
 (D)
(D)
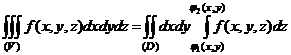
Если областью (D) является круг, то при вычислении внешнего двойного интеграла переходят к полярным координатам x = ρ∙ cosφ, y = ρ∙sinφ. Тогда