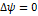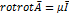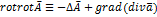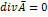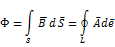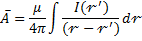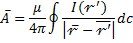Основные уравнения магнитной статики
Основные уравнения магнитной статики


 ДУ ИН.УР
ДУ ИН.УР





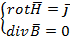
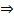
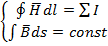
3 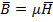
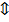 вне зоны токов
вне зоны токов
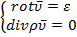 1.
1. 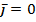
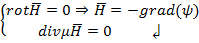
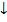
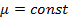
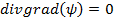
|
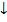
Частный случай задач магнитной статики
-задачи Ливиофе и Неймана
основн.ур-ние магнитной статики для областей занятых током
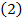
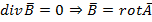
D 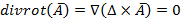
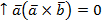
|
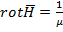
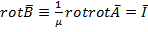
|
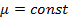
Известно вект. тождество
|
Усл.Кулона чтобы магнит. потоки были всегда замкнуты.
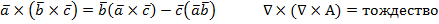
Основное ур-ние магнитной статики для облости занятой током свод к вект для ур-ния Пуасона сводится к "3" ур-ниям Пуасона.
|
1 Магнит поток есть инт от магнит индукц по поверх или опред чотера
2 Легче всего решается задачи Неймона и Дирихле
пример: Найти векторный потенциал произвольной катушки с током в векторном пространстве


 Задача Дирихле
Задача Дирихле 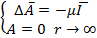 (5) S
(5) S 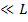 A-?
A-?
 L
L 
|
|
! Если сечение S проволоки много меньше L
Потенциал точечного заряда
Потенциал поля точечного заряда Q можно найти с помощью: 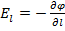
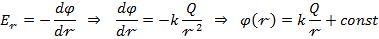
Обычно потенциал принимают равным нулю на бесконечности. В этом случае: 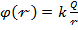
Физический смысл потенциала - работа по переносу заряда из точки в бесконечность.







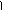


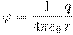 потенциал точечного заряда.
потенциал точечного заряда. 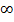
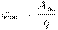 A
A
Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.
Потенциал φ∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:
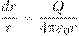
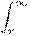
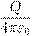
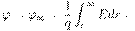
18 нету
Электромагнитные поля в проводящих средах
Эксперименты показали, что в проводящей среде электромагнитные поля распространяются медленно.
Квазистатические уравнения:
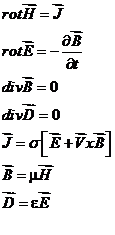
Случай неподвижных проводников.

Уравнение распространения электромагнитных волн в проводящей среде сводится к параболическим уравнениям математической физики.
Аналогично:
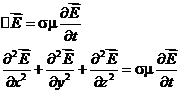
Для движущихся сред, когда
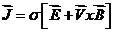
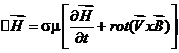
 20.Магнитное число Рейнольдса
20.Магнитное число Рейнольдса
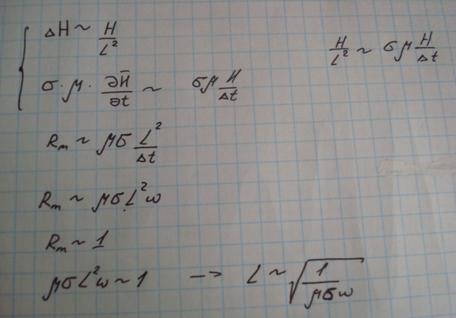 |
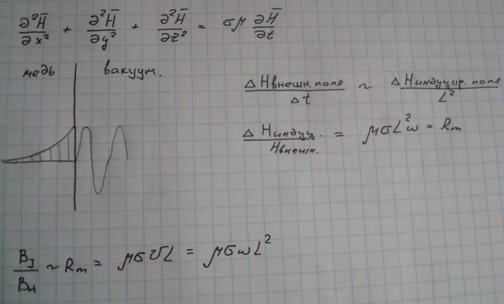 Физический смысл
Физический смысл
Магнитное число Рейнольдса-отношение индуцированных полей в проводящей среде к внешнему полю.
21.Проникновение магнитного поля в проводящую среду.
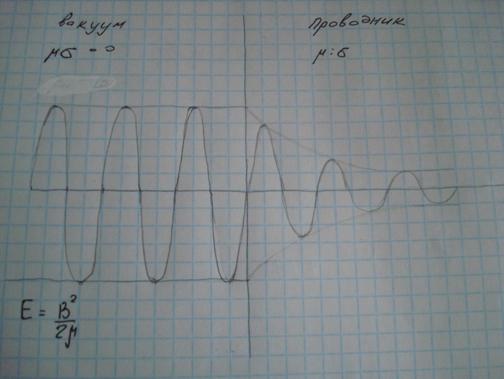
Уравнение диф.магнитного поля:
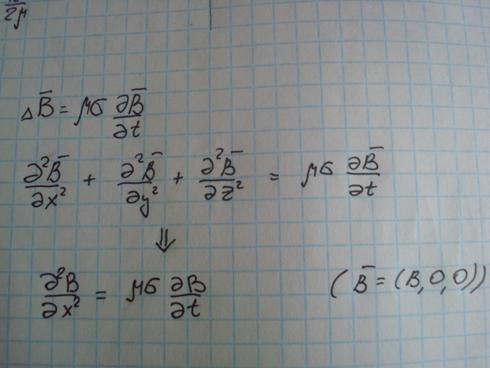
(1*)
1)Начальные условия-гармоническая волна.
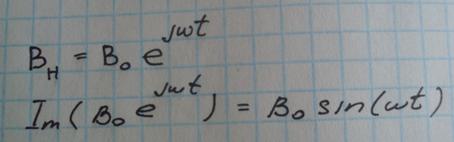 |
2)Граничные условия:
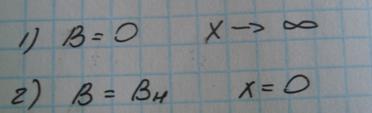 |
3)Вид решения:
Из-за того,что волна гармоническая решение можно представить в виде (2*)
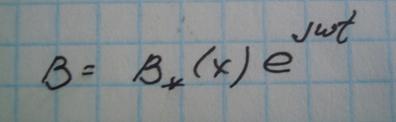 |
4)Подставляем (2*)в (1*)
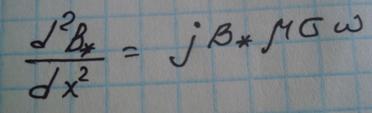
(3*)
Это ОДУ 2го порядка.
Решение:
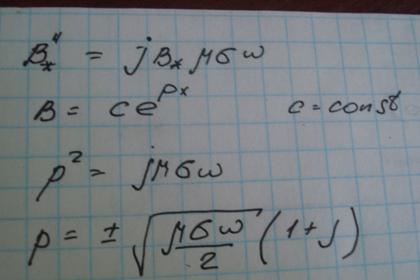 (4*)
(4*)
Общее решение:
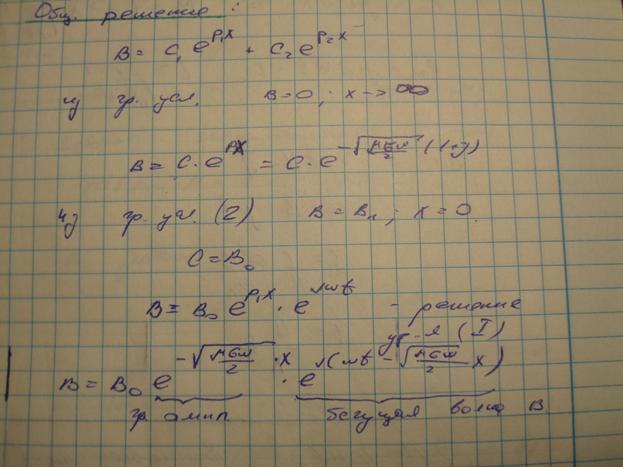
 Фазовая скорость:
Фазовая скорость:
Глубина проникновения:
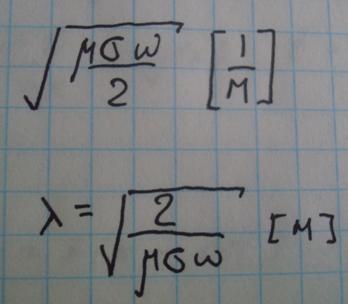
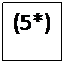 Глубина проникновения-масштаб на котором поле убывает в е раз.
Глубина проникновения-масштаб на котором поле убывает в е раз.
(5*) через магн.число Рейнольдса:
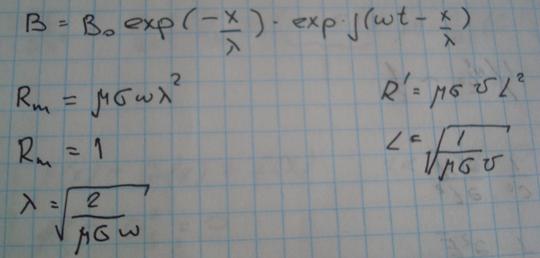
Поперечные волны
Для поперечных волн в бесстолкновительной плазме, температурой электронов в которой пренебрегается, диэлектрическая проницаемость имеет вид[2]:
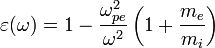
Поскольку масса ионов значительно выше, чем масса электронов, вторым слагаемым в скобках обычно можно пренебречь. Таким образом, эти волны являются аналогом электромагнитных волн в вакууме, однако отличаются от них наличием дисперсии. Дисперсионное соотношение для этих волн имеет вид[3]:
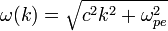
Откуда несложно определить фазовую и групповую скорости волн:
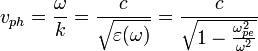
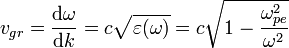
Таким образом, всегда выполняется соотношение 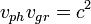 . Особенностью поперечных волн в изотропной плазме является также наличие диапазона частот
. Особенностью поперечных волн в изотропной плазме является также наличие диапазона частот 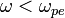 , в котором диэлектрическая проницаемость отрицательна, а коэффициент преломления чисто мнимый. Волны с такой частотой не могут распространяться в плазме. При падении на слой плазмы электромагнитной волны, частота которой ниже электронной плазменной частоты, в плазме образуется скин-слой, а волна полностью отражается.
, в котором диэлектрическая проницаемость отрицательна, а коэффициент преломления чисто мнимый. Волны с такой частотой не могут распространяться в плазме. При падении на слой плазмы электромагнитной волны, частота которой ниже электронной плазменной частоты, в плазме образуется скин-слой, а волна полностью отражается.
Учёт кинетических эффектов, в том числе температуры электронов (в случае нерелятивистских температур), приводит только к небольшой коррекции дисперсионного соотношения для поперечных волн, но не привносит новых свойств или эффектов. Это объясняется тем, что скорость поперечных волн значительно выше, чем скорость теплового движения электронов[4].
Продольные волны
Продольные являются особым видом волн, характерным только для плазмы и плазмоподобных сред. Эти волны называются продольными, поскольку в них вектор электрического поля сонаправлен с волновым вектором. Характерной особенностью является также то, что наравне с колебаниями поля в ленгмюровских волнах колеблется электронная плотность. Ленгмюровские волны были впервые изучены в 1929 году И. Ленгмюром и Л. Тонксом (англ.).
Важной особенностью ленгмюроских волн является наличие у них так называемого затухания Ландау — бесстолкновительного затухания, связанного с передачей энергии волн частицам плазмы. Коэффициент затухания зависит от длины волны и в длинноволновом приближении, так что выполняется 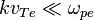 (где
(где 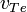 — тепловая скорость электронов), равен[5]:
— тепловая скорость электронов), равен[5]:
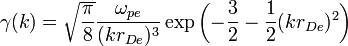
где 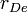 — дебаевский радиус электронов.
— дебаевский радиус электронов.
В том же приближении дисперсионное соотношение для продольных волн имеет вид:
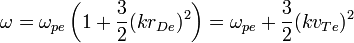
Таким образом, коротковолновые возмущения, для которых 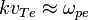 , быстро затухают, поскольку для них величина частоты приближается к величине коэффициента затухания, то есть волна, фактически, перестаёт быть распространяющейся и затухает на одном периоде. При этом в той области, где волна затухает слабо, её частота практически не изменяется и приблизительно равна электронной плазменной частоте. Это позволяет говорить о том, что данная волна является просто плазменными колебаниями, распространяющимися в пространстве только за счёт наличия тепловой скорости электронов. В приближении нулевой температуры электронов скорость ленгмюровских волн точно равна нулю, а дисперсионное соотношение для них имеет вид[:
, быстро затухают, поскольку для них величина частоты приближается к величине коэффициента затухания, то есть волна, фактически, перестаёт быть распространяющейся и затухает на одном периоде. При этом в той области, где волна затухает слабо, её частота практически не изменяется и приблизительно равна электронной плазменной частоте. Это позволяет говорить о том, что данная волна является просто плазменными колебаниями, распространяющимися в пространстве только за счёт наличия тепловой скорости электронов. В приближении нулевой температуры электронов скорость ленгмюровских волн точно равна нулю, а дисперсионное соотношение для них имеет вид[:
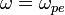
Поскольку ленгмюровские волны связаны с колебаниями электронной плотности, которые происходят на высоких частотах, движение ионов слабо сказывается на характеристиках продольных волн. Фактически, движение ионов даёт вклад только в малую поправку к плазменной частоте[7]:
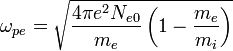
Теорема Умова-Пойнтинга.
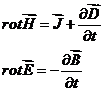
Умножим почленно первое на 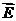 , второе на
, второе на 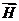 и вычтем второе из первого:
и вычтем второе из первого:
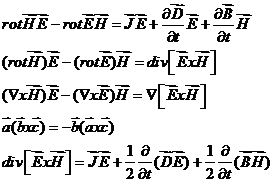
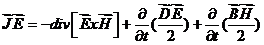 - дифференциальная теорема Умова-Пойнтинга.
- дифференциальная теорема Умова-Пойнтинга.
Проинтегрируем последнее по 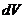 :
:
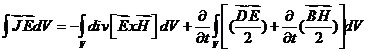
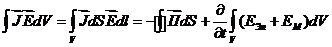 , где
, где 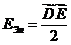 , а
, а 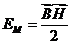 ,
,
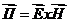 - вектор Умова-Пойнтинга
- вектор Умова-Пойнтинга
Выведенные формулы 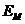 и
и 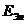 верны только тогда, когда материальные уравнения линейны. В общем случае это не так.
верны только тогда, когда материальные уравнения линейны. В общем случае это не так.
Теорема Умова-Пойнтинга в интегральной форме утверждает – чтобы получить энергию из заданного объёма, нужно обеспечить разряд конденсаторов или индуктивных накопителей.
Теорема Умова-Пойнтинга имеет громадное научно-техническое значение, поскольку доказывает материальность ЭМП.
27 нету
Выпрямители
Выпрямитель — устройство, предназначенное для преобразования энергии источника переменного тока в постоянный ток.[1]
[]Инверторы
Инвертор — устройство, задача которого обратна выпрямителю, то есть преобразование энергии источника постоянного тока в энергию переменного тока.
Инверторы подразделяются на два класса: ведомые сетью (зависимые) и автономные.
Зависимые инверторы
Ведомые инверторы преобразуют энергию источника постоянного тока в переменный с отдачей её в сеть переменного тока, то есть осуществляют преобразование, обратное выпрямителю.[2]
]Автономные инверторы
Автономные инверторы — устройства, преобразующие постоянный ток в переменный с неизменной или регулируемой частотой и работающие на автономную (не связанную с сетью переменного тока) нагрузку.[3]
В свою очередь автономные инверторы подразделяются на:
§ АИН
§ АИТ
§ АИР
Преобразователь частоты — вторичный источник электропитания, вырабатывающий переменный электрический ток с частотой, отличной от частоты тока исходного источника.
Классификация:
По способу управления
1. Импульсные (на постоянном токе)
2. Фазовые (на переменном токе)
По типу схем
§ Нулевые, мостовые
§ Трансформаторные, бестрансформаторные
§ Однофазные, двухфазные, трёхфазные…
По способу управления
§ Управляемые
§ Неуправляемые
Примеры накопителей энергии
1. Конденсаторный накопитель [2]
При емкости конденсатора 1 Ф и напряжении 250 В запасенная энергия составит: E = CU2 /2 = 1 ∙ 2502 /2 = 31.25 кДж ~ 8.69 Вт · час. Если использовать электролитические конденсаторы, то их масса может составить 120 кг. Удельная энергия накопителя при этом 0.26 кДж/кг. При работе накопитель может в течение часа обеспечивать нагрузку не более 9 Вт. Срок службы электролитических конденсаторов может достигать 20 лет. Ионисторы по плотности запасаемой энергии приближаются к химическим аккумуляторным батареям. Достоинства: накопленная энергия может быть использована в течение короткого промежутка времени.
2. Гравитационные накопители
Копрового типа [5]. Вначале поднимаем тело массой 2000 кг на высоту 5 м. Затем тело опускается под действием силы тяжести, вращая электрогенератор. E = mgh ~ 2000 ∙ 10 ∙ 5 = 100 кДж ~ 27.8 Вт · час. Удельная энергия 0.05 кДж/кг. При работе накопитель может в течение часа обеспечивать нагрузку не более 28 Вт. Срок службы накопителя может составлять 20 и более лет. Достоинства: накопленная энергия может быть использована в течение короткого промежутка времени.
Гидравлический. Вначале перекачиваем 10 т воды из подземного резервуара (колодца) в емкость на вышке. Затем вода из емкости под действием силы тяжести перетекает обратно в резервуар, вращая турбину с электрогенератором. Легко обеспечить разницу высот 10 м. Тогда E = mgh ~ 10000 ∙ 10 ∙ 10 = 1 МДж = 0.278 кВт · час. Удельная энергия 0.1 кДж/кг. При работе накопитель может в течение часа обеспечивать нагрузку не более 280 Вт. Срок службы накопителя может составлять 20 и более лет. Достоинства: при использовании ветродвигателя последний может непосредственно приводить в движение водяной насос, вода из емкости на вышке может использоваться для других нужд.
3. Маховик [3, 4]
Энергия, запасаемая в маховике, может быть найдена по формуле E = 0.5 J w2 , где J - момент инерции вращающегося тела.
Для цилиндра радиуса R и высотой H:
J = 0.5 p r R4 H
где r - плотность материала, из которого изготовлен цилиндр.
Предельная линейная скорость на периферии маховика Vmax (составляет примерно 200 м/с для стали).
Vmax = wmax R или wmax = Vmax /R
Тогда Emax = 0.5 J w2max = 0.25 p r R2 H V2max = 0.25 M V2max
Удельная энергия составит: Emax /M = 0.25 V2max
Для стального цилиндрического маховика максимальная удельная энергия составляет приблизительно 10 кДж/кг. Для маховика массой 100 кг (R = 0.2 м, H = 0.1 м) максимальная накопленная энергия может составлять 0.25 ∙ 3.14 ∙ 8000 ∙ 0.22 ∙ 0.1 ∙ 2002 ~ 1 МДж ~ 0.278 кВт · час. При работе накопитель может в течение часа обеспечивать нагрузку не более 280 Вт. Срок службы маховика может составлять 20 и более лет. Достоинства: накопленная энергия может быть использована в течение короткого промежутка времени, характеристики могут быть существенно улучшены [3, 4].
4. Химическая аккумуляторная батарея [1]
Свинцово-кислотная аккумуляторная батарея емкостью 190 А · час с выходным напряжением 12 В при 50 % разрядке может выдавать ток величиной 10 А примерно 9 часов. Запасенная энергия составляет 12 ∙ 10 ∙ 9 = 1.08 кВт · час ~ 3.9 МДж за цикл. При массе батареи 70 кг удельная энергия составит 56 кДж/кг. При работе аккумулятор может в течение часа обеспечивать нагрузку не более 1080 Вт. Срок службы аккумулятора составляет 3 ... 5 лет. Достоинства: от аккумулятора можно получать непосредственно электрическую энергию, выходной ток может достигать величины порядка тысячи ампер, выходное напряжение 12 В соответствует автомобильному стандарту, имеется множество устройств, работающих непосредственно от источника постоянного напряжения 12 В, имеются преобразователи 12/220 В различной мощности [8, 9].
5. Пневматический накопитель
В стальной резервуар емкостью 1 м3 закачивается воздух под давлением 50 атмосфер. Чтобы выдержать такое давление, стенки резервуара должны иметь толщину примерно 5 мм. Сжатый воздух используется для выполнения работы. При изотермическом процессе работа A, совершаемая идеальным газом при расширении в атмосферу, определяется формулой [12]:
A = (M / m ) R T ln (V2 / V1 )
где M - масса газа, m - молярная масса газа, R - универсальная газовая постоянная, T - абсолютная температура, V1 - начальный объем газа, V2 - конечный объем газа. С учетом уравнения состояния для идеального газа (P1 V1 = P2 V2 ) для данной реализации накопителя V2 / V1 = 50, R = 8.31 Дж/(моль · град), T = 293 0K, M / m ~ 50 : 0.0224 ~ 2232, работа газа при расширении 2232 ∙ 8.31 ∙ 293 ∙ ln 50 ~ 20 МДж ~ 5.56 кВт · час за цикл. Масса накопителя примерно равна 250 кг. Удельная энергия составит 80 кДж/кг. При работе пневматический накопитель может в течение часа обеспечивать нагрузку не более 5.5 кВт. Срок службы пневматического накопителя может составлять 20 и более лет. Достоинства: накопительный резервуар может быть расположен под землей, в качестве резервуара могут использоваться стандартные газовые баллоны в требуемом количестве с соответствующим оборудованием, при использовании ветродвигателя последний может непосредственно приводить в действие насос компрессора, имеется достаточно большое количество устройств, напрямую использующих энергию сжатого воздуха.
Помимо рассмотренных существуют и другие накопители энергии, например, индукционные, пружинные, тепловые.
Простейшим и наиболее распространённым индуктивным преобразователем, с помощью которого переменный ток одного напряжения преобразуется в переменный ток другого напряжения, является трансформатор
Индуктивные преобразователи электроэнергии, в которых имеются движущиеся части, называются электромашинными преобразователями.
В зависимости от рода тока ЭМ разделяются на машины постоянного и переменного тока. Трансформатор и простейшая ЭМ могут преобразовывать только электроэнергию переменного тока, которая поступает из сети с переменным напряжением, изменяющимся с частотой f. Для того чтобы преобразовать с помощью трансформатора или ЭМ электроэнергию постоянного тока, нужно превратить её с помощью преобразователя частоты (ПЧ) того или иного типа в электроэнергию переменного тока. Такой преобразователь может быть полупроводниковым, в ЭМ – также и механическим (в виде коллектора, пластины которого соединены с катушками вращающейся обмотки, и неподвижных щёток, касающихся пластин).
Основные уравнения магнитной статики


 ДУ ИН.УР
ДУ ИН.УР





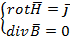
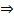
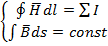
3 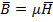
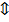 вне зоны токов
вне зоны токов
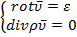 1.
1. 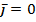
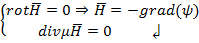
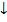
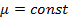
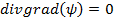
|
Частный случай задач магнитной статики
-задачи Ливиофе и Неймана
основн.ур-ние магнитной статики для областей занятых током
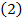
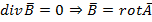
D 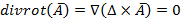
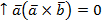
|
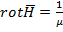
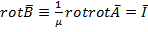
|
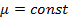
Известно вект. тождество
|
Усл.Кулона чтобы магнит. потоки были всегда замкнуты.
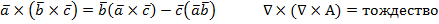
Основное ур-ние магнитной статики для облости занятой током свод к вект для ур-ния Пуасона сводится к "3" ур-ниям Пуасона.
|
1 Магнит поток есть инт от магнит индукц по поверх или опред чотера
2 Легче всего решается задачи Неймона и Дирихле
пример: Найти векторный потенциал произвольной катушки с током в векторном пространстве
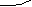



 Задача Дирихле
Задача Дирихле  (5) S
(5) S 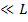 A-?
A-?
 L
L 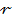
|
|
! Если сечение S проволоки много меньше L
Потенциал точечного заряда
Потенциал поля точечного заряда Q можно найти с помощью: 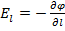
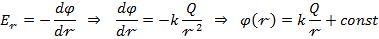
Обычно потенциал принимают равным нулю на бесконечности. В этом случае: 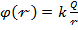
Физический смысл потенциала - работа по переносу заряда из точки в бесконечность.









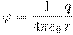 потенциал точечного заряда.
потенциал точечного заряда. 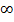
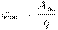 A
A
Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.
Потенциал φ∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:
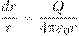
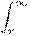
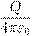
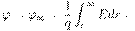
18 нету