Степенным рядом называется функциональный ряд вида

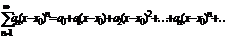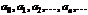, где -постоянные числа, называемые коэффициентами ряда, 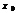-фиксированное число.При 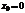получаем степенной ряд вида

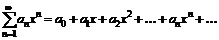. Ряд (1) легко приводится к ряду (2), если положить 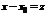. Поэтому при изучении степенных рядов иногда ограничиваются степенным рядом (2).

Выясним вопрос о сходимости степенного ряда (7.3). Область сходимости этого степенного ряда содержит, по крайней мере, одну точку 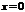(ряд (1) сходится в точке ).

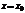Об области сходимости степенного ряда можно судить, исходя из следующей теоремы.Теорема (теорема Абеля). Если степенной ряд (7.3) сходится в точке 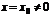, то он абсолютно сходится при всех 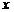, удовлетворяющих неравенству 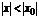.Из теоремы Абеля следует, что если 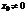есть точка сходимости степенного ряда, то интервал 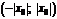весь состоит их точек сходимости данного ряда; при всех значениях вне этого интервала ряд (7.3) расходится.Пусть 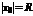. Интервал 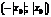или 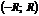называют интервалом сходимости. Число 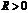называют радиусом сходимости степенного ряда. Таким образом, 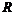- это такое число, что при всех 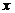, для которых 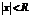, ряд (7.3) абсолютно сходится, а при 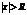ряд расходится .Отметим, что на концах интервала сходимости (т.е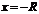. при и при 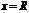) сходимость ряда проверяется в каждом случае отдельно.В частности, когда ряд (7.3) сходится лишь в одной точке 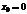, то считаем, что 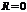. Если же ряд (7.3) сходится при всех значениях 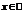(т.е. во всех точках числовой оси), то считаем, что .

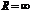Для нахождения радиуса сходимости степенного ряда (7.3) можно поступить следующим образом. Составим ряд из модулей членов данного степенного ряда

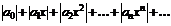
и применим к нему признак Даламбера. Допустим, что существует предел

.

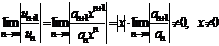По признаку Даламбера ряд сходится, если 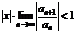, т.е. ряд сходится при тех значениях , для которых

.

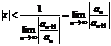Ряд, составленный из модулей членов ряда (7.3), расходится при тех значениях , для которых .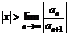

Таким образом, для ряда (7.3) радиус сходимости

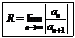. (7.4)

Аналогично, воспользовавшись радикальным признаком Коши, можно получить, что

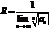. (7.5)

Замечания:Если 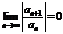, то ряд (7.3) абсолютно сходится на всей числовой оси. В этом случае 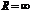. Если 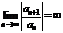, то .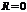

Если дан степенной ряд (7.2), то его радиус сходимости определяется также по формулам (7.4) или (7.5), а интервал сходимости будет интервал с центром в точке : .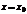

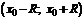Свойства степенных рядов.

Сформулируем без доказательства основные свойства степенных рядов.

1)Сумма степенного ряда (7.3) является непрерывной функцией в интервале сходимости .

2)Степенные ряды и , имеющие радиусы сходимости соответственно и , можно почленно складывать, вычитать и умножать. Радиус сходимости произведения, суммы и разности рядов не меньше, чем меньшее из числе и .

3)Степенной ряд внутри интервала сходимости можно почленно дифференцировать. Для ряда

при

. (7.6)

4)Степенной ряд можно почленно интегрировать на каждом отрезке, расположенном внутри интервала сходимости. Для ряда (7.3) при выполняется равенство

Ряды (7.6) и (7.7) имеют тот же радиус сходимости, что и исходный степенной ряд. Перечисленные свойства остаются справедливыми и для степенных рядов вида .

Ряды Тейлора и Маклорена.

Для приложений важно уметь данную функцию представлять в виде суммы степенного ряда.Для любой функции , определенной в окрестности точки и имеющей в ней производные до -го порядка включительно, справедлива формула Тейлора:

,

где , - остаточный член в форме Лагранжа. Причем число можно записать в виде , где .

Формулу (7.8) можно записать в виде

,

где - многочлен Тейлора.

Если функция имеет производные любых порядков (т.е. бесконечно дифференцируема) в окрестности точки и остаточный член стремится к нулю при ( ), то из формулы Тейлора получается разложение функции по степени , называемое рядом Тейлора:

Если в ряде Тейлора положить , то получим разложение функции по степеням в так называемый ряд Маклорена:

Отметим, что ряд Тейлора можно формально построить для любой бесконечно дифференцируемой функции (это необходимое условие) в окрестности точки . Но отсюда еще не следует, что он будет сходиться к данной функции ;он может оказаться расходящимся или сходится, но не к функции .

В следующей теореме (которую примем без доказательства) сформулировано необходимое и достаточное условие сходимости ряда Тейлора к функции .

Теорема Для того чтобы ряд Тейлора (7.9) функции сходился к функции в точке , необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора (7.8) стремился к нулю при 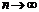, т.е. чтобы .

Для разложения функции в ряд Маклорена (7.10) нужно:

1. найти производные ;

2. вычислить значения производных в точке ;

3. выписать ряд (7.10) для заданной функции и найти его интервал сходимости;

4. найти интервал , в котором остаточный член ряда Маклорена при 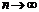. Если такой интервал существует, то в нем функция и сумма ряда Маклорена совпадают.