ПОВИ-2 по замкнутым поверхностям. Формула Астроградского.

Вычисление поверхностного интеграла II рода сводится к вычислению двойного интеграла по плоской области.Справедлива следующая формула, сводящая вычисление интеграла (3.4) к вычислению двойного интеграла:

где - проекции поверхности на плоскость , - нормальный вектор к поверхности , которая задана функцией . Причем в двойном интеграле переменную надо заменить на .

Поверхностный интеграл II рода в формуле (3.4) можно записать иначе:

. Пусть функция непрерывна во всех точках поверхности , которая задана непрерывной функцией в замкнутой области -проекции поверхности на плоскость . Тогда справедлива следующая формула:

При этом перед двойным интегралом берется знак «+», если , и знак «-», если .

Если поверхность задана непрерывной функцией в замкнутой области - проекции поверхности на плоскость . Тогда справедлива следующая формула:

При этом перед двойным интегралом берется знак «+», если , и знак «-», если .

Если поверхность задана непрерывной функцией в замкнутой области - проекции поверхности на плоскость . Тогда справедлива следующая формула:

.

При этом перед двойным интегралом берется знак «+», если , и знак «-», если .

Понятие скалярного поля. Поверхности и линии уровня.

Полем называется область пространства, в каждой точке которой определено значение некоторой величины.Если каждой точке этой области определено число , говорят, что в области определено (задано) скалярное поле или функция точки. Иначе можно сказать, что скалярное поле – это скалярная функция вместе с ее областью определения.Если каждой точке области пространства соответствует некоторый вектор , то говорят, что задано векторное поле или векторная функция точки.Если функция или не зависят от времени, то скалярное или векторное поле называется стационарным (или установившимся). Поле, которое меняется с течением времени (например, меняется скалярное поле температуры при охлаждении тела), называется нестационарным (или неустановившимся).

Скалярное поле

Если в области 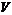задана скалярная функция точки , то говорят, что в этой области задано скалярное поле.Если - область трехмерного пространства, то скалярное поле можно рассматривать как функцию трех переменных - координат точки , т.е.

.

Если скалярная функция зависит только от двух переменных 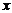и , то соответствующее скалярное поле называют плоским.

В дальнейшем будем предполагать, что скалярная функция - определяющая скалярное поле, непрерывна вместе со своими частными производными.Для наглядного представления скалярного поля используют поверхности и линии уровня.

Поверхностью уровня скалярного поля называется геометрическое место точек, в которых функция принимает постоянное значение, т.е.

. В случае плоского поля равенство представляет собой уравнение линии уровня поля – линии на плоскости , в точках которой функция сохраняет постоянное значение.

Пусть скалярное поле задано функцией , где значения

откладываются по оси . Линиями уровня на плоскости будут проекции линий, которые получаются в пересечении поверхности с плоскостями (см. рисунок).

Линии уровня применяются в математике при исследовании поверхностей методом сечений.

Свойства Grad :

1) Производная в данной точке по направлению вектора имеет наибольшее значение, если направление вектора совпадает с направлением градиента, когда , т.е. при ; это наибольшее значение производной равно .Таким образом, направление градиента есть направление наискорейшего возрастания функции. В противоположном направлении функция будет быстрее всего убывать. - наибольшая скорость изменения функции в точке .

2) Производная по направлению вектора, перпендикулярного к вектору , равна нулю.

3) Градиент функции в каждой точке направлен по нормали к поверхности уровня скалярного поля, проходящего через эту точку.

4) .

5) , где .

6) и др.