Опр-ие двойного интеграла, его геом. смысл. Св-ва

Геом. смысл:

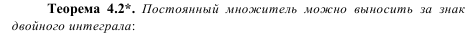
Св-ва:∫∫0*dx*dx=0; ∫∫dxdy=SД; ∫∫(f(x,y)+/- g(x,y))dxdy=∫∫(f(x,y)dxdy+/- ∫∫g(x,y))dxdy; ∫∫C*f(x,y))dxdy=C*∫∫f(x,y))dxdy
Повторные интегралы. Вычисление 2-ых интегралов.
Двойной интеграл от непрерывной функции
Вычисление: провести прямую, || Оу; внутренний интеграл зависит от у, где прямая 1-ый раз пересекает обл. наз. точкой входа, выходит - точка выхода. Нижний предел внутреннго интеграла – ф-ция, график которой содержит точку входа, верхний – выхода. Внешний интеграл – числа. Если инт-ем по 1-ой переменной, все остальные – пост.числа.
z= f(x,y) по правильной области D равен двукратному интегралу от этой функции по области D : если D – область правильная в направлении оси Oy, то
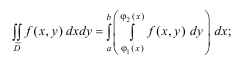
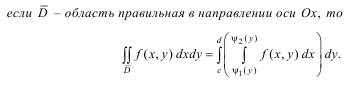
Применение двойных интегралов в геометрии.
Объем тела, ограниченного поверхностью z = f (x, y), где f (x, y) ≥ 0, плоскостью z = 0 и с боковых сторон цилиндрической поверхностью, у которой образующие параллельны оси Oz,а направляющей служит граница области D , вычисляется по формуле:
V=∫∫f(x,y))dxdy
Если D – правильная область, то ее площадь вычисляется по формуле:S=∫∫dxdy
Основные понятия оДУ. Т. о сущ-и и ед-ти. Задача Коши. Общий интеграл и общее решение ДУ. Частные решения. Геом. смысл ДУ.
ДУ называется уравнение, связывающее независимую переменную x, искомую функцию у=ϕ (х) и ее производные y′, y′′,..., y(n). F (х, у, у′, у′′, ...,у n )=0. Порядком ДУназывается порядок наивысшей производной, входящей в уравнение. Решением или интегралом ДУназывается всякая функция y = ϕ(x), которая, будучи подставленной в уравнение, превращает его в тождество.
Т. о существовании и единственности решенияДУ. Если в уравнении y’=f(x,y) функция f (x, y) и ее ЧП ∂f/∂y непрерывны в некоторой области D на плоскости Оху, содержащей некоторую точку (x0, y0) , то существует единственное решение этого уравнения y = ϕ(x), удовлетворяющее условию: y = y0 при x = x0.Получение решения уравнения при заданных начальных условиях (x0, y0)∈D называется решением задачи Коши соответствующего уравнения для начальных условий (x0, y0)∈D . Решение ДУ с нач. условиями – решение задачи Коши.
Общим решением ДУпервого порядка называется функция y=ϕ(x,C). Частным решением ДУназывается любая функция y = ϕ(x,C0), которая получается из общего решения y = ϕ(x,C). Геом. смысл:в случае невыполнения хотябы одного из условий торемы сущ-я, через любую точку плоскости может проходить не одно решение, а можт н проходить вообще; общий интеграл представляет собой семейство кривых на координатной плоскости, зависящее от одной произвольной постоянной C (или, как говорят, от одного параметра С). Эти кривые называются интегральными кривыми данного ДУ. Общим решением ДУ наз. ф-ция, равная y=y(x,C), кот. Зависит от х, удовл. условия:эта ф-ция –ршение при любом С. Частному решению соответствует одна кривая этого семейства, проходящая через некоторую заданную точку плоскости. РешениеДУ, не получающееся из общего интеграла ни при каком значении C и имеющее своим графиком огибающую семейства интегральных кривых, входящих в общее решение, называется особым решением ДУ.
