Пусть сущ завис-ть для 2-х переем-х, выраженная с пом таблицы, получ экспериментально

X … …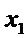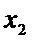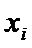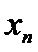

Y … …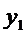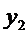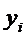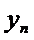

Требуется наилуч образом сгладить эксперимент завис-ть м/д переем-ми х и у, т.е. установить зав-ть м/д х и у в виде формулы y = f(x).

О. Формулы, служ для аналитич представлений эксперимент данных, называются эмпирическими.

Задача нах-я эмпирич формул разбивается на 2 этапа.

I этап

Устанавливается вид зависимости y = f(x) (линейная, квадратичная, логарифмическая и т.д.).

II этап

Опред-ся неизв пар-ры этой ф-ии. Для этого применяют наиболее распр и теоретически обоснованный метод наименьших квадратов. Он состоит в следующем:

В кач-ве неизв пар-ра ф-и f(x) выб-т такие знач-я, чтобы суммы кв-тов невязок ( 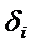) была мин. Невязка ( 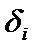) – это –откл-е от «теоретич» знач-й 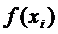, найд по эмпирич формулам y = f(x) от соответствующих опытных знач-й 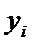. Рассм-м функцию 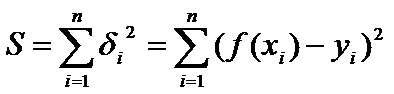(т.е. сумму квадратов всех невязок) Пусть в кач-ве ф-и у = f(x) взята лин ф-я у = ax + b. Тогда задание сводится к отыскиванию пар-ов a и b, при кот ф-я 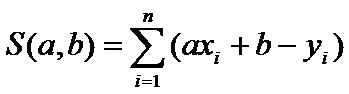принимает наим зн-е. 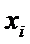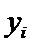Очевидно, что S = S(a,b) есть ф-я 2-х переем-х a и b, а и - пост числа, полученные экспериментально.

Т. о., достаточно исслед-ть ф-ю S = S(a,b) на экстремумах. Находим частные производные

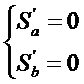или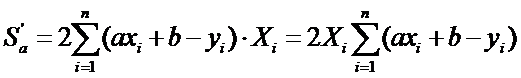

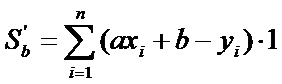
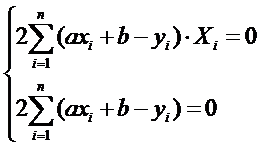
После преобразований, система принимает вид:

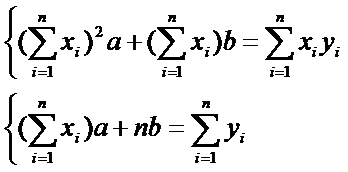(**) Система (**) - система норм уравнений 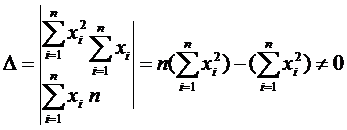т.к квадрат ∑ >∑-мы квадратов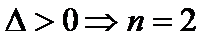

Ф-я S = S(a,b) достигает своего min при a и b, найд из сист (**). Для этого проверим достаточные условия экстремума: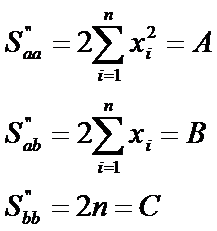

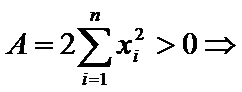функция достигает min (глобальный min).

6.Неопред интеграл, первообразная и их св-ва.

Пусть функции f(x) и F(x) определены на интервале (a;b). Если функция F(x) имеет производную на интервале (a;b) и для всех x ? (a;b) выполняется равенство F’(x) = f(x), то функция F(x) называется первообразной функции f(x) на интервале (a;b). Т.: Если F(x) первооб-я ф-и f(x), то F(x)+С тоже пер-я. О. Мн-во всех перв-х ф-й F(x)+С для данной ф-и f(x) наз. неопред интегр ф-и f(x) обозн-ся

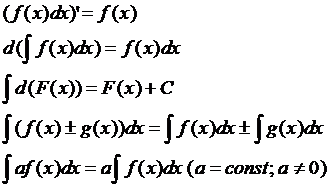
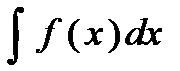
Св-ва НИ:

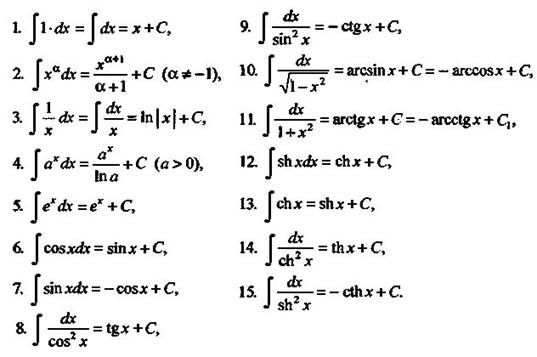
7. Интегрир-е путем замены переменной (подстановкой)

М-д подстановки

∫f(x)dx= [x=φ(t),t=ψ(x),dx=φ’(t)dt] =∫f(φ(t)φ’(t)dt

Если интеграл непосредственно не вычисляется,можно применить метод,кот. состоит в след.:

-вводится новая переменная

x=φ(t),где t=ψ(x) явл. обратной по отношению к φ(t), dx=φ’(t)dt- дифференциал ф-ции x=φ(t)

Если подстановка выбрана удачно, то интеграл, получ в правой части, вычисляется проще, чем в исходной.

Если ф-ция x=φ(t) непрерывна и монотонна,то обратн. t=ψ(x) всегда сущ.

Вычислив интеграл в правой части по t,следует вернуться к переменной x

∫f(ψ(x)) φ’(x)dx=∫f(t)dt, где t=ψ(x)

1 ∫f(ax+b)dx= ax+b=t, x=(t-b)/a

dx=1/a dt

=∫f(t)1/a dt=1/a ∫f(t)dt=1/a F(t)+C=

=1/a F(ax+b)+C

2 ∫ f’(x)/f(x) dx= ln f(x) +C

3 ∫ df(x)/f(x) = ln f(x) +C

Метод интегрирования по частям

Задано: U=U(x), V=V(x),известно: d(UV)=VdU+UdV

проинтегрируем обе части уравнения:

∫ d(UV)= ∫ VdU+ ∫ UdV

UV=∫ VdU+ ∫ UdV=> ∫UdV=UV-∫VdU- ф-ла интегр-я по частям

Смысл ф-лы интегр-я по частям сост в след.: подинтегр выраж-е UdV разб-ся на 2 части т. о.,чтобы интеграл в правой части вычислялся проще,чем исходный.

Основные классы ф-ций,интегрируемых по частям:

1 ∫ ln^m(x)dx, ∫arcsin^mxdx, ∫arccos^m xdx,∫arctg^m xdx

2 ∫Pn(x)lnaxdx,∫Pn(x)e^axdx,∫ Pn(x)sinaxdx,

∫Pn(x)cosaxdx

3 ∫e^axsinbxdx,∫e^axbxdx

4 ∫ (x²+a²)½dx, ∫(a²- x²)½dx, ∫ dx/(x²+a²)^k