Лабораторная работа 1. исследование дисперсии волн
Лабораторная работа 1. ИССЛЕДОВАНИЕ ДИСПЕРСИИ ВОЛН
В ВОЛНОВОДЕ И В КОАКСИАЛЬНОЙ ЛИНИИ ПЕРЕДАЧИ
Цели работы. Ознакомление с законами распространения СВЧ-сиг-налов в ограниченных средах (коаксиальной и волноводной регулярных линиях передачи). Получение практических навыков измерения СВЧ-сигналов.
Основные положения
Фазовая скорость (vф) и длина волны (λв) в линии передачи могут отличаться от соответствующих величин для свободного пространства (c; λв). Из анализа дисперсионных уравнений можно получить:
где λкр– длина волны в свободном пространстве; εr, μr– относительные диэлектрическая и магнитная проницаемости среды; λкр– критическая длина волны в линии передачи; с – скорость света в вакууме.
Для линий с воздушным заполнением εr= μr=1 и
Наиболее распространенными типами линий передач в СВЧ-диапазоне являются коаксиальная линия и прямоугольный волновод.
Коаксиальная линия передачи. В коаксиальной линии (рис. 1.1, а) могут распространяться волны как дисперсионного, так и бездисперсионного типов. Волной бездисперсионного типа является ТЕМ-волна, для которой λкр= ∞ и λв= λ0.
Структура поля ТЕМ волны показана на рис. 1.1, б. ТЕМ-волна является основной для коаксиальной линии.
Прямоугольный волновод. В прямоугольном волноводе (рис. 1.2, а) могут распространяться только волны дисперсионного типа Hтри Eтр.Для них
,
где a, b – поперечные размеры волновода.
Наименьшую величину λкримеет волна H10(волн типов Eт0и E0nне существует), называемая основной модой. Структура поля волны H10 показана на рис. 1.2, б.
Длину волны λкри частотную дисперсию легко измерить, создавая стоячую волну. Для этого можно, например, расположить в поперечном сечении волновода проводящую стенку (короткое замыкание – КЗ) или образовать в каком-то сечении режим холостого хода (ХХ). Эпюры Еполя приведены на рис. 1.3: а – в режиме короткого замыкания и б – в режиме холостого хода. Для КЗ Г равен –1, для ХХ Г равен +1 (Г – коэффициент отражения).
Порядок выполнения работы
1. Собрать схему:
§ соединить СВЧ-кабелем выход генератора и вход измерительной линии;
§ телевизионным кабелем соединить выход головки детектора и вход усилителя осциллографа.
2. Включить генератор и осциллограф. Дать прогреться приборам в течение 5 мин.
3. Установить режим работы генератора . Ручкой «MHz» установить нужную частоту f.
4. Установить пределы измерения на осциллографе 1 мВ/см; 0.5 мс/дел.
5. Получить изображение меандра на экране осциллографа:
§ установить ручкой нониуса каретку зонда измерительной линии в среднее положение;
§ ручками настройки получить меандр с амплитудой 2..3 деления осциллографа.
6. Вращая ручку нониуса измерительной линии, отыскать 3 – 4 максимума стоячей волны.
7. Проделать операции пп. 3 – 6 в диапазоне частот 2.5…4.0 ГГц через 100 МГц на коаксиальной и на волноводной линиях. Результаты занести в таблицу.
Содержание отчета
1. Цель работы.
2. Теоретические сведения.
3. Блок-схема измерений.
4. Результаты измерений, сведенные в таблицу.
5. Графики λв= F(f) (измеренные и рассчитанные по формулам) для коаксиальной и для волноводной линий.
6. Выводы.
Основные положения
 |
Микрополосковая линия (МПЛ) (рис. 2.1, а) – это двухпроводная полосковая линия с поперечным сечением в виде параллельных прямых, имеющая одну плоскость симметрии, параллельную направлению распространения энергии (на рис. 2.1, а: 1 – проводящая полоска, 2 – экран (земляной электрод), 3 – подложка из диэлектрика). МПЛ – в настоящее время наиболее широко применяемая СВЧ-линия передачи при разработке миниатюрных устройств СВЧ. Основным типом в МПЛ является квазиТЕМ-волна, однако могут быть возбуждены и волны высших типов. Структура поля в поперечном сечении МПЛ показана на рис. 2.1, б.
Одной из важнейших характеристик МПЛ является волновое сопротивление, определяемое геометрическими размерами линии и диэлектрической проницаемостью подложки. Для полосок нулевой толщины (t/h→0)
при 
;
при 
,
где εэф– эффективная диэлектрическая проницаемость. В статическом случае 
.
Одним из простейших и в то же время важнейших элементов СВЧ-схем на основе МПЛ является микрополосковый резонатор (МПР), представляющий собой отрезок МПЛ резонансной длины l. По конструкции МПР делятся на замкнутые (например, кольцевой), а также на короткозамкнутые и на разомкнутые на конце. Короткозамкнутые на концах МПР используются редко из-за технологических трудностей обеспечения короткого замыкания между проводниками МПЛ. На рис. 2.2 показаны примеры а ‑ линейного разомкнутого на концах МПР, б ‑ кольцевого МПР. Основными характеристиками резонатора являются резонансная частота f0 и добротность Q. Экспериментально эти характеристики могут быть получены на основе измерения характеристик передачи резонатора. Резонансная частота МПР определяется длиной резонатора l и диэлектрической проницаемостью подложки. Для линейного резонатора (рис. 2.2, а)
, (2.1)
где n = 1,2,… – число полуволн, укладывающихся на длине резонатора; εэф– эффективная диэлектрическая проницаемость.
 |
Нагруженная добротность резонатора определяется как
, где 
– ширина резонансной кривой, измеренная по уровню 3 дБ от максимума. Для МПР характерны невысокие значения добротности (100…500). Основные преимущества МПР – миниатюрность, совместимость с линиями передачи СВЧ и активными планарными элементами (диодами, транзисторами и т.д.).Порядок выполнения работы
Содержание отчета
1. Схемы экспериментальной установки.
2. Тип и основные характеристики панорамного измерителя КСВ и ослаблений.
3. Краткое описание объектов исследования и эскиз, поясняющий их конструкцию.
4. Результаты измерений параметров МПР:
§ частотная характеристика передачи резонатора с указанием резонансной частоты и частот, соответствующих краям полосы, по которым определяется добротность;
§ значение добротности резонатора;
§ значение εэф, рассчитанные по (2.1) из измеренных значений резонансной частоты и длины резонатора.
5. Результаты исследования МПЛ:
§ зависимость длины волны в МПЛ от частоты;
§ распределение поля вдоль МПЛ.
6. Выводы.
|
Лабораторная работа 3. ОПРЕДЕЛЕНИЕ ПОЛНОГО СОПРОТИВЛЕНИЯ ЭЛЕМЕНТОВ СВЧ-ТРАКТА С ПОМОЩЬЮ ИЗМЕРИТЕЛЬНОЙ ЛИНИИ
Цели работы. Изучение методов измерения полных сопротивлений. Освоение практических приемов работы с измерительной линией и круговой диаграммой полных сопротивлений.
Основные положения
Измерения коэффициента отражения и полного сопротивления узлов или элементов СВЧ-трактов необходимы при решении задач согласования, определении параметров эквивалентных схем и частотных характеристик устройств СВЧ.
Измерения с помощью измерительной линии (ИЛ) являются наиболее простыми, достаточно точными и доступными при экспериментальном определении коэффициента отражения и полного сопротивления.
Принцип таких измерений основан на известной зависимости между сопротивлением исследуемого элемента и распределением напряженности электрического поля волны вдоль однородной линии передачи, соединяющей измеряемый элемент с генератором. Если сопротивление элемента Zнравно волновому сопротивлению линии Z0, то в линии устанавливается режим бегущей волны (отсутствуют отраженные волны). При Zн≠ Z0в передающей линии устанавливается режим стоячих волн (суперпозиция падающих и отраженных волн). Коэффициент отражения определяется отношением напряженности электрического поля отраженной волны E0к напряженности падающей волны Eпв месте расположения элемента, т. е.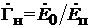 
. В общем виде коэффициент отражения является комплексным числом: 
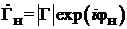, где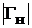 
– модуль отношения напряжений; φн– фазовый сдвиг между падающей и отраженной волнами на исследуемом объекте.
Комплексный коэффициент отражения связан с полным сопротивлением (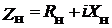 
) соотношением 
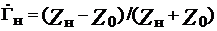. Как правило, сопротивление элементов СВЧ-трактов выражают в приведенных значениях:
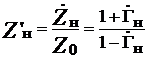. (3.1)
На практике обычно измеряют коэффициент стоячей волны (КСВ) напряжения, определяемый отношением максимального значения напряжения стоячей волны в линии к ее минимальному значению: 
, и положение ближайшего от нагрузки минимума напряжения в линии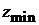 
. Через эти параметры можно легко определить модуль и фазу коэффициента отражения:
; 
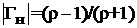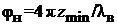(3.2)
где λв– длина волны в волноводе, определяемая соотношением:
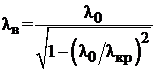. (3.3)
здесь λкр– критическая длина волны волновода.
Для основного типа волны прямоугольного волновода (TE10) λкр= 2a, где a – размер широкой стенки волновода.
С учетом соотношений (3.1)–(3.2) можно найти полное сопротивление исследуемого элемента:
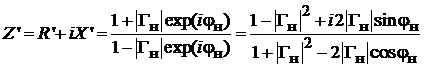. (3.4).
Полное сопротивление удобно определять с помощью круговых диаграмм полных сопротивлений, где все указанные параметры ( 
) связаны с сеткой активных и реактивных составляющих сопротивления.
Порядок выполнения работы
1. Ознакомиться с аппаратурой, входящей в экспериментальную установку.
2. Изучить конструкцию и основные характеристики измерительной линии (ИЛ).
3. Изучить круговую диаграмму полных сопротивлений и методику определения с ее помощью полного сопротивления и проводимости.
4. Включить измерительный генератор согласно инструкции и настроить на заданную преподавателем частоту.
5. Настроить измерительную линию на заданную частоту. Для этого собрать схему (см. рис. 3.1), заменив в ней исследуемый элемент на короткозамыкатель. От генератора подать в линию высокочастотный сигнал и с помощью ручек настройки диодной и зондовой резонансных камер ИЛ получить максимум на шкале индикаторного прибора. При этом глубину погружения зонда следует устанавливать минимальной с учетом реальной чувствительности индикатора. Уровень мощности в ИЛ следует поддерживать таким, чтобы показания индикатора соответствовали полной шкале при установке зонда в максимум напряженности электрического поля.
6. Измерить распределение напряженности электрического поля вдоль линии при подключенном короткозамыкателе и при замене его на согласованную нагрузку. Определить длину волны в линии и сравнить с расчетной (формула (3.3)).
7. Провести измерения, необходимые для определения полного сопротивления нагрузок. Для этого зафиксировать положение Z1 одного из минимумов напряженности поля при подключенном короткозамыкателе. Затем собрать схему согласно рис. 3.1 и определить положение минимума Z2, ближайшего к ранее найденному Z1 со стороны нагрузки. Относительный фазовый сдвиг определяется соотношением 
. Для определения КСВ необходимо: установить зонд в положение минимума и зафиксировать показания индикатора (U1); затем, установив зонд в положение максимума, увеличить затухание встроенного в генератор аттенюатора до получения прежних показаний индикатора (U1) и определить разность в децибелах по шкале аттенюатора: 
. Значения КСВ в децибелах определяется ΔA и с учетом того, что 
, получим 
.
8. Повторить пп. 4 – 7 на других частотах (по указанию преподавателя).
9. Определить полное сопротивление и проводимость исследованного элемента, используя круговую диаграмму и результаты измерений ( 
).
10. Рассчитать активные и реактивные составляющие полного сопротивления, используя соотношения (3.2) – (3.4).
Содержание отчета
1. Схема измерительной установки.
2. Основные технические характеристики измерительных приборов.
3. Графики распределения напряженности электрического поля вдоль линии при подключении согласованной нагрузки, короткозамыкателя и исследуемого элемента. На графиках указать значение λвКСВ.
4. Эскиз исследуемого элемента с указанием основных геометрических размеров.
5. Основные элементы круговой диаграммы с нанесенными на ней значениями экспериментально найденных точек, определяющих 
и 
.
6. Выводы.
Лабораторная работа 4. НЕВЗАИМНЫЕ ФЕРРИТОВЫЕ УСТРОЙСТВА: ФАРАДЕЕВСКИЙ ВРАЩАТЕЛЬ
ПЛОСКОСТИ ПОЛЯРИЗАЦИИ
Цель работы. Ознакомление с эффектом необратимого вращения плоскости поляризации электромагнитной волны, проходящей через линию передачи, содержащую феррит.
Основные положения
Общие сведения о ферритах. Ферриты – это группа содержащих ионы железа материалов, которые обладают одновременно магнитными свойствами ферромагнетиков и электрическими свойствами диэлектриков (εr= 5…20, 
). Свойства ферритов в значительной степени определяются их структурой. Наибольшее применение получили ферриты со структурой шпинели (например, железоникелевый феррит NiFe2O3, марганцевый феррит MnO×Fe2O3) и со структурой граната (например, железоиттриевый гранат Y3Fe5O12– ЖИГ). Благодаря наличию ионов железа ферриты обладают большой магнитной проницаемостью и спонтанной намагниченностью. На рис. 4.1 показана кривая намагничивания ферромагнитного материала.
В ненамагниченном состоянии феррит представляет собой конгломерат областей, магнитные моменты которых ориентированы в различных направлениях. Под воздействием переменного магнитного поля магнитные моменты указанных областей отклоняются в направлении вектора H, в результате появляется вектор магнитной поляризации (вектор намагниченности, определяемый как магнитный момент единицы объема), совпадающий с вектором напряженности внешнего поля, и магнитная проницаемость является скалярной величиной. Поэтому свойства ненамагниченного феррита для переменных полей любого направления одинаковы и распространение электромагнитных волн в нем происходит так же, как в любой другой изотропной среде.
Постоянное магнитное поле Н0ориентирует магнитные моменты атомов железа вдоль поля, в результате чего феррит приобретает анизотропные свойства, а его магнитная проницаемость для переменных электромагнитных полей становится тензорной величиной. Слабое переменное магнитное поле h, перпендикулярное намагничивающему полю Н0, заставляет магнитные моменты прецессировать вокруг вектора Н0(рис. 4.2).
Если постоянное поле направлено вдоль оси z (Н0= еzН0), а переменное поле h ему перпендикулярно (h= exhx+eyhy), тензор магнитной проницаемости насыщенного феррита имеет вид
,
где 
, 
( 
, 
, w0– собственная частота прецессии магнитного момента электрона в постоянном поле Н0; М0– спиновый магнитный момент электрона).
Вектор магнитной индукции электромагнитной волны b связан с вектором напряженности магнитного поля h соотношением b = ||m|| hили bx= = m0(m’ hx‑ ik hy), by= m0(ik hx+ m’ hy), bz= m0hz= 0.
Итак, компоненты тензора ||m|| зависят от напряженности постоянного поля, и поэтому векторы b и h имеют различные соотношения между компонентами. Отсюда следует важное свойство намагниченного феррита – вращение плоскости поляризации электромагнитной волны, которое называется эффектом Фарадея.
 |
Вращение плоскости поляризации в волноводе, содержащем намагниченный феррит. Рассмотрим круглый цилиндрический волновод, содержащий продольно намагниченный ферритовый стержень (рис. 4.3). Пусть в волноводе возбуждается волна типа Н11. Будем считать, что присутствие ферритового стержня не искажает распределение поля в поперечном сечении волновода и что частота много больше собственной частоты прецессии (в этом случае активными потерями в феррите можно пренебречь).
Пусть также на вход устройства подается плоскополяризованная волна (плоскость поляризации – это плоскость, составленная вектором Е и направлением распространения волны). Плоскополяризованную волну можно представить в виде суммы двух распространяющихся в противоположных направлениях волн круговой поляризации с противоположным направлением вращения векторов напряженности поля. Действительно, напряженность магнитного поля плоскополяризованной волны можно записать как
.
На рис. 4.4 показано графически разложение плоскополяризованной волны на две волны круговой поляризации с амплитудой 1/2Нm.
Благодаря анизотропии феррита условия распространения волн с разными направлениями вращения различны; соответственно, различны и фазовые скорости каждой из волн (b+¹ b‑) и различны набеги фазы на длине z. В результате плоскость поляризации реальной волны Н11 постепенно поворачивается по мере движения волны вдоль волновода, причем угол поворота Q плоскости поляризации пропорционален расстоянию z от входной плоскости, и зависит от намагничивающего поля Н0, частоты СВЧ-сигнала w, а также от размеров и материала от ферритового стержня: Q = hkz, где h - коэффициент пропорциональности, учитывающий геометрические размеры и диэлектрические характеристики феррита, .
Для w>>w0, 
, так что 
.
Следует отметить, что направление вращения плоскости поляризации не зависит от направления движения электромагнитной энергии по волнов-ду, т. е. ферритовый вращатель плоскости поляризации является невзаимным устройством.
Порядок выполнения работы
1. Собрать схему в соответствии с рис. 4.5.
2. Установить ручки приборов в следующие положения:
§ генератор СВЧ-сигналов Г4-83:
- кнопки управления амплитудой сигнала отжаты;
- ручку «Уровень» в крайнее левое положение;
- частота 9.4 ГГц;
§ блок питания постоянного тока:
- напряжение 4 В;
- ток 0 А;
- ручку «Усиление» в положение, соответствующее минимальной чувствительности.
3. Включить приборы и дать им прогреться в течение 5…10 мин.
4. На панели генератора Г4-83 нажать кнопку .
5. Увеличивая выходную мощность генератора ручкой «Уровень» и чувствительность осциллографа, установить на экране осциллографа развертку огибающей СВЧ-сигнала (меандр) в пределах половины экрана.
6. Перемещая рупор приемной антенны вдоль направляющей, найти положения минимума и максимума принимаемого сигнала.
7. Установить рупор приемной антенны на расстоянии, соответствующем максимуму принимаемого сигнала.
8. Измерить зависимость регистрируемого сигнала от угла поворота рупора (0…180°).
9. Измерить зависимость принимаемого сигнала от угла поворота рупора при трех значениях тока управления (10; 30; 60мА).
10. Выключить ток. Установить угол поворота рупора, соответствующий минимальному принимаемому сигналу.
11. Измерить зависимость угла поворота Q рупора, соответствующего минимальному сигналу, от тока управления(0; 10; 20; 40; 60 мА).
12. Изменить направление тока. Повторить измерения по пп. 9‑11.
13. Вернуть ручки приборов в исходное положение.
14. Выключить приборы.
Содержание отчета
1. Схема экспериментальной установки.
2. Графики зависимости амплитуды огибающей СВЧ-сигнала от угла поворота рупора при различных значениях тока через катушку на частоте 9.4 ГГц.
3. График зависимости угла поворота плоскости поляризации электромагнитной волны от управляющего тока на частоте 9.4 ГГц.
4. Выводы.
Лабораторная работа 5. Исследование широкополосного согласования сопротивления нагрузки и СВЧ-генератора
Цель работы:Расчет с помощью программы PUFF схемы двухэлементного четвертьволнового согласующего тракта, обеспечивающего широкополосное согласование генератора СВЧ-сигнала и нагрузки.
Основные положения
Одной из важнейших задач техники СВЧ является согласование сопротивления нагрузки с источником СВЧ-мощности (т. е. минимизация отражения СВЧ-сигнала от полезной нагрузки). Для решения этой задачи традиционно используются различные согласующие схемы как на основе сосредоточенных элементов, так и на основе распределенных линий. Наиболее часто используемыми схемотехническими решениями при согласовании сопротивления нагрузки Zнс СВЧ-трактом являются согласующие линии с электрической длиной, равной λ/4 (одиночные или соединенные последовательно). Теоретический анализ распределенных линий основан на использовании телеграфных уравнений. Можно показать, что для линии передачи длиной l с волновым сопротивлением Z0, нагруженной на сопротивление Zн(рис. 5.1), справедлива формула трансформации сопротивлений:
(5.1)
где β = 2π/λ = 2πfε0.5∙c‑1– фазовая постоянная распространения.
Данное соотношение справедливо в случае отсутствия потерь в линии передачи. В ситуации, когда длина линии равна λ/4 (такая линия является трансформатором сопротивления) выражение (5.1) упрощается: 
(Z0переобозначили как Zтр). Тогда можем записать сопротивление трансформатора: 
.
Для увеличения частотной полосы согласования применяют каскадное соединение трансформаторов (рис. 5.2). Теоретический анализ показывает, что при двухкаскадном соединении трансформаторов волновые сопротивления каждого из них могут быть определены, исходя из следующих соотношений:
 |
; 
. 
В интегральных схемах СВЧ используются планарные линии передачи, плоские проводники которых формируются на поверхности диэлектрической подложки методами интегральной технологии с применением фотолитографии для получения необходимого рисунка топологии. Наибольшее применение нашла микрополосковая линия (МПЛ), поперечное сечение которой представлено на рис. 5.3. МПЛ относится к категории линий со слоистым диэлектриком (диэлектрическая подложка – воздух), для которых вводится понятие эффективной диэлектрической проницаемости: 
, где с – скорость света в свободном пространстве; vф – фазовая скорость волны в линии передачи. Введение εэф позволяет описывать рассматриваемую линию как некоторую эквивалентную, имеющую такие же геометрические размеры, но однородное диэлектрическое заполнение. Эквивалентность линий определяется равенством в них фазовых скоростей. Эффективная диэлектрическая проницаемость характеризует соотношение между энергией, концентрирующейся в воздухе рядом с полоском, и энергией, концентрирующейся в диэлектрике.
Основным типом волны в МПЛ является квазипоперечная Т-волна, содержащая в основном поперечные компоненты, поэтому параметры идеальной МПЛ обычно рассчитывают в квазистатическом приближении, пренебрегая продольными составляющими. Тем не менее наличие продольных компонентов приводит к тому, что в реальной МПЛ имеет место частотная дисперсия, или зависимость фазовой скорости от частоты. При частотах выше 10 ГГц значительно увеличивается влияние продольных составляющих поля. Следствием этого является частотная зависимость эффективной диэлектрической проницаемости.
Программа PUFF содержит модели МПЛ, которые позволяют вести расчет как в приближении идеальной линии, так и с учетом потерь и частотной дисперсии.
При пренебрежении толщиной полоска выражения для волнового сопротивления линии и эффективной диэлектрической проницаемости (при условиях εr < 16 и w/h < 1 можно записать в виде
, (5.2)
. (5.3)
Для тех же условий, но при w/h > 1 выражения приобретут следующий вид:
, (5.4)
. (5.5)
Порядок выполнения работы
1. Запустить программу “MathCAD”.
§ в соответствии с вариантом из таблицы (по указанию преподавателя) рассчитать: а) одноэлементную согласующую цепь; б) двухэлементную согласующую цепь, содержащую два трансформатора. Определить волновые сопротивления трансформаторов;
Варианты заданий к лабораторной работе
| Вариант | Zн, Ом |  f, ГГц |
§ рассчитать по формулам (5.2) – (5.5) физические длину и ширину трансформаторов, выполненных в виде отрезков микрополосковой линии передачи.
2. Запустить программу PUFF:
§ в окне топологии «LAYOUT» нарисовать отрезок МПЛ с заданными параметрами и соединить один его конец с внешним входом 1, а другой – со входом 2, имеющими волновое сопротивление 
(окно подложки «BOARD»). В окне анализа «PLOT» выполнить расчет коэффициентов передачи S21 и отражения S11 устройства в полосе частот 1…10 ГГц. Исследовать характер амплитудно-частотной характеристики (АЧХ) устройства;
§ выполнить согласование заданной нагрузки, описанной в виде сосредоточенного элемента («lumped»), при помощи одного четвертьволнового трансформатора. Сохранив результаты расчета, построить частотную зависимость коэффициента отражения для двухэлементной согласующей цепи. Скорректировать для обоих случаев геометрические размеры линий, рассчитанные по приближенным формулам.
Содержание отчета
1. Цель работы.
2. Геометрические размеры элементов согласующих цепей, рассчитанные по приближенным формулам.
4. Построенные на одном графике частотные зависимости модуля коэффициента отражения для одноэлементной и для двухэлементной согласующих цепей.
5. Выводы.
Список рекомендуемой литературы
Гольдштейн Л. Д., Зернов Н. В. Электромагнитные поля и волны. М.: Сов. радио, 1971.
Гупта К., Гардж Р., Чадха Р. Машинное проектирование СВЧ-устройств. М.: Радио и связь, 1987.
Никольский В. Д., Никольская Т. И. Электродинамика и распространение радиоволн. М.: Наука, 1989.
Шимони К. Теоретическая электротехника. М.: Мир, 1964.
Фуско В. СВЧ-цепи анализ и автоматизированное проектирование. М.: Радио и связь, 1990.
 |
СОДЕРЖАНИЕ
| Лабораторная работа 1. Исследование дисперсии волн в волноводе и в коаксиальной линии передачи.......................... | .........3 |
| Лабораторная работа 2. Микрополосковые линии передачи ......... | .…....7 |
| Лабораторная работа 3. Определение полного сопротивления элементов СВЧ-тракта с помощью измерительной линии............ | .........14 |
| Лабораторная работа 4. Невзаимные ферритовые устройства: фарадеевский вращатель плоскости поляризации....................... | .........17 |
| Лабораторная работа 5. Исследование широкополосного согласования сопротивления нагрузки и СВЧ-генератора............ | .........23 |
| Список рекомендуемой литературы………………………………… | ……..27 |
Редактор И. Б. Синишева
__________________________________________________________________
Подписано в печать 14.12.2006. Формат 60х84/16. Бумага офсетная.
Печать офсетная. Гарнитура "Times New Roman".
Печ. л. 1,75. Тираж 140 экз. Заказ
Издательство СПбГЭТУ "ЛЭТИ"
197376, С.-Петербург, ул. Проф. Попова, 5
Лабораторная работа 1. ИССЛЕДОВАНИЕ ДИСПЕРСИИ ВОЛН