Гидравлический расчет простых трубопроводов.

Гидравлический расчет простых трубопроводов.

Простой трубопровод

Расчет простого трубопровода между двумя резервуарами

Расчет простого трубопровода при истечении в атмосферу

Сифонный трубопровод. Вакуум на участке трубопровода.

Использование приблизительных зависимостей при расчете простого трубопровода.

Замена местных сопротивлений на сопротивление трубы с эквивалентной длиной.

Определение величины критического напора

Определение величины критического напора

Три задачи на расчет простого трубопровода

Методика построения графика напоров

Простой трубопровод

Трубопровод без ответвлений потока называют простым. Простой трубопровод может иметь различные диаметры и включать местные сопротивления.

Трубопровод называют сложным, если он содержит параллельные соединения и разветвления простых трубопроводов.

Движение жидкости в простом трубопроводе происходит за счет разности напоров в резервуарах: питателе и приемнике или в разности напоров в питателе и в струе на выходе трубопровода. Разность напоров (удельная энергия для движения жидкости) может быть обеспечена также за счет работы насоса или давления газа, например, при закачке газа над поверхностью жидкости.

Движение называется установившимся, если разность напоров не меняется во время движения жидкости.

На участках простого трубопровода происходит преодоление сопротивлений и потеря напора.

На рис.12.1 изображен простой трубопровод, произвольно расположенный в пространстве, состоящий из нескольких участков с длиной l_i и диаметром d_i и содержащий местные сопротивления.

Уравнение Бернулли для сечений «1-1» и "2-2".

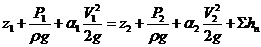(12.1),

где z₁ и z₂ – геометрические напоры, относительно произвольно выбранной плоскости сравнения, Р₁ и Р₂- избыточные давления в сечениях, V₁ и V₂ –скорости в сечениях, Σh_П – сумма потерь на трение по длине и в местных сопротивлениях, а также потерь на трение по длине.

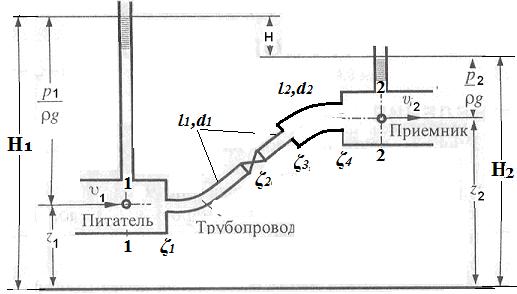
Рис.12.1. Схема простого трубопровода.

Гидростатическим напором называется сумма геометрического и пьезометрического напора в данном сечении трубопровода. Разность гидростатических напоров в сечениях 1 и 2

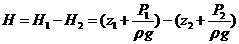, (12.2)

где z – геометрический напор, P/ρg - пьезометрический напор.

Располагаемым напором - Н_расп называется разность гидростатических напоров в сечениях 1 и 2, если величина этой разности Н₁-Н₂ для сечений 1 и 2 известна.

Потребным напором – Н_потр называется разность гидростатических напоров_, если величина разности Н₁-Н₂ не известна и ее необходимо определить.

Сифонный трубопровод. Вакуум на участке трубопровода.

Определение коэффициентов сопротивления трубы в зависимости

От режима течения жидкости.

При расчете трубопроводов коэффициенты ξ местных сопротивлений и коэффициента трения λ выбираются в зависимости от режима движения жидкости.

1. Ламинарный режим, Re ≤ 2300, коэффициент трения λл=64/Re.

Для определения потерь на трение используем формулу Дарси:

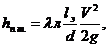(12.15)

Если подставить λ=64/Re в формулу (12.15) для потерь на трение

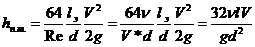(12.16) ,

получим для ламинарного режима потери в функции первой степени скорости.

Если в эту формулу подставить скорость через расход V =Q/F = 4Q/(πd²), получим потери через расход в первой степени

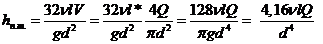(12.17).

Можно определять потери, используя скорость или расход.

2.Турбулентный режим.

А. Область гидравлически гладких труб, 20d/Δэ ≥Re > 2300,

где Δэ –эквивалентная абсолютная шероховатость.

При Re≤10⁵ коэффициент сопротивления трению по формуле Блазуиса

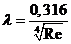, (12.18)

При Re>10⁵ по формуле Конакова

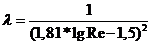(12.19)

Величина λ может быть вычислена по этим формулам или взята из таблиц в задачнике на стр.228.

Подставляя формулу Блазиуcа в формулу Дарси для области гидравлически гладких труб получим

(12.20)

До чисел Рейнольдса близких к границе Re_{г.гл.тр.} ~ 20d/Δ к этой области могут быть отнесены цельнотянутые трубы из цветных (Δ <0,1мм) металлов, а также качественные стальные трубы.

Б. Переходная область, при 500 d/Δ ≥Re ≥ 20d/Δ.

Коэффициент λ в переходной области зависит и от числа Re и от эквивалентной шероховатости Δэ. Значения λ в функции Re и относительной гладкости d/Δэ по данным теплотехнического института, приведены в справочниках или могут быть взяты по графику Мурина.

Для определения коэффициента λ применяется формула Альтшуля.

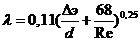(12.21)

Средние значения эквивалентной шероховатости для новых стальных труб Δ =0,1мм, для бывших в употреблении до Δ = 0,2 мм.

В. Область гидравлически шероховатых труб, при Re ≥ 500 d/Δэ.

Коэффициент в области гидравлически шероховатых труб λ зависит только от относительной шероховатости Δэ, которая входит в формулы для λ в виде отношения Δэ/d.

Формулу Шифринсона

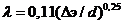( 12.22 )

Для старых стальных и чугунных труб, абсолютная шероховатость может иметь значение до Δ = 1 мм, тогда формула для

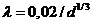( 12.23 )

Зависимость λ от d/Δэ для квадратичной области дается также по таблицам, например в задачнике на стр.229.

По графику Мурина величина λ для турбулентного режима составляет от 0,01 до 0,04

От режима течения жидкости.

При ламинарном режиме движения и малых числах Re= < 2300, в потоке преобладают силы вязкостного трения над силами инерции, коэффициенты сопротивления зависят от числа Re

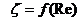
На рис.12.6. показаны изменение коэффициентов сопротивления для входа в трубу, угольник, вентиль в функции числа Re. При числе Rе = <100 зависимость ζ =f(Re) почти линейна. При увеличении Re>10⁴ коэффициенты принимают постоянные значения.

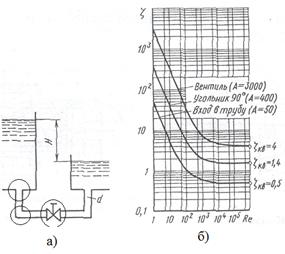
Рис.12.6 Коэффициенты местных сопротивлений при ламинарном режиме течения. а) вход в трубу, угольник, вентиль; б) графики изменения коэффициентов в функции числа Рейнольдса.

Гидравлический расчет простых трубопроводов.

Простой трубопровод