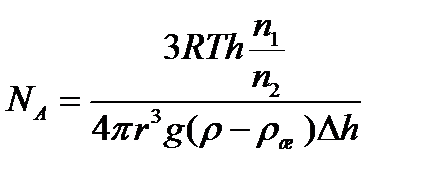Среднеарифметическая скорость движения молекул. Средняя кинетическая энергия поступательного движения одной молекулы идеального газа.
Средняяарифметическаяскорость
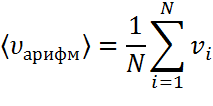
Имеет и другой вид:
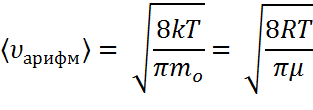
Средняя кинетическая энергия поступательного движения одной молекулы идеального газа
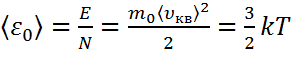 .
. 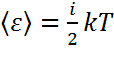
Отсюда следует, что 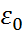 =0 при T = 0 K – прекращается движение молекул газа.
=0 при T = 0 K – прекращается движение молекул газа.
Молекулярно-кинетическое толкование температуры: термодинамическая температура – есть мера средней кинетической энергии поступательного движения молекул газа.
Барометрическая формула. Распределение Больцмана.
Пусть мы находимся на уровне моря(нулевой уровень). 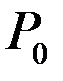 -давление на этой поверхности.
-давление на этой поверхности.
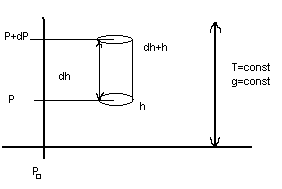 При
При 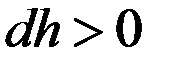 :
: 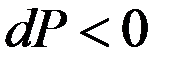 . Предположим, что площадь основания цилиндра ровна 1.
. Предположим, что площадь основания цилиндра ровна 1. 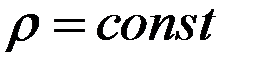 для
для 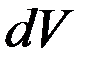 .
.
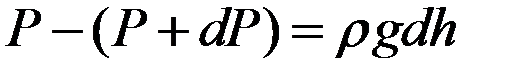 , т.к.
, т.к. 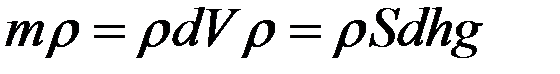 . Если
. Если 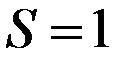 , то
, то 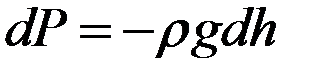 ,
, 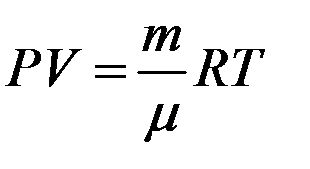 ,
, 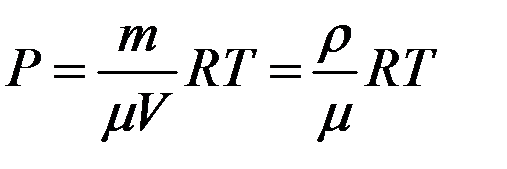 ,
, 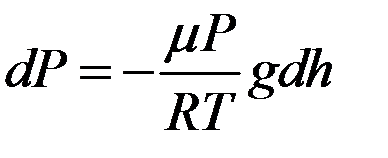 ,
, 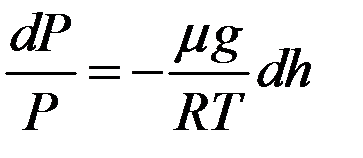 ,
, 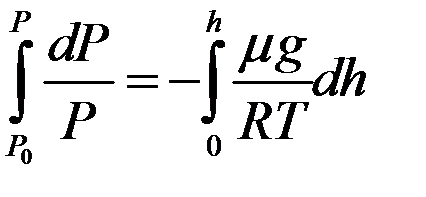 ,
, 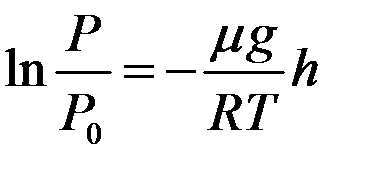 ,
, 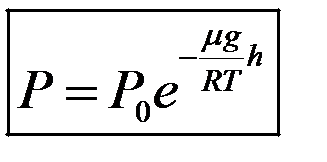 -барометрическая формула,
-барометрическая формула,  ,
, 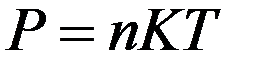 ,
, 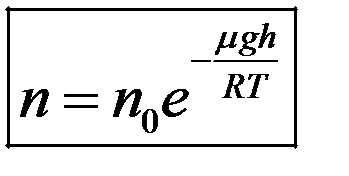 -распределение Больцмана.
-распределение Больцмана.
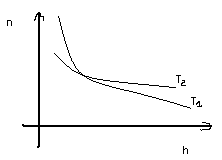 При
При 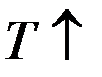 ,
, 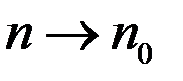 (Т-повышается)
(Т-повышается) 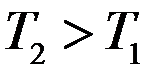 .
.
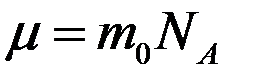 ,
, 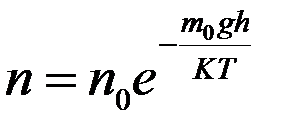 (*). Величина
(*). Величина 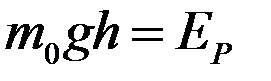 -потенциальная энергия, кот. обладает молекула на данной высоте. Тогда
-потенциальная энергия, кот. обладает молекула на данной высоте. Тогда 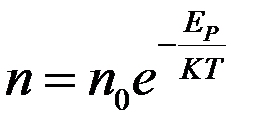 ,
, 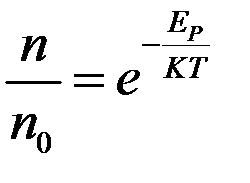 -доля молекул для высоты
-доля молекул для высоты 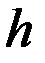 с энергией
с энергией 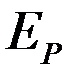 .
.
Существ. в атмосфере распределения молекул воздуха по высоте устанавливается в результате действия двух факторов: 1) под действием силы тяжести молекула стремится опустится на поверхность Земли. 2) Тепловое движение, характеризуемое величиной  , стремится распределить молекулы равномерно по высотам.
, стремится распределить молекулы равномерно по высотам.
Формула (*) определяет распределение молекул по высоте и выражает также распределение их по значениям потенц. энергии справедливо не только для поля силы тяжести, но и для любого поля потенц. сил.
Опытное обоснование МКТ (опыт Штерна, броуновское движение, опыт Ламмерт, опытное определение постоянной Авогадро).
Эксперименты, подтверждающие молекулярно-кинетическую теорию.
1. Броуновское движение. Любые частицы малых размеров, взвешенные в газе или жидкости, совершают сложное зигзагообразное движение.
Броуновское движение взвешенных частиц вызывается ударами молекул среды, в которой частицы взвешены. Подтверждение гипотезы о хаотическом тепловом движении молекул.
2. Опыт Штерна. Два коаксиальных цилиндра синхронно
вращаются в вакууме.
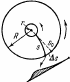 Атомы серебра, испарясь с проволоки, расположенной вдоль оси внутреннего
Атомы серебра, испарясь с проволоки, расположенной вдоль оси внутреннего
цилиндра, вылетают через щель и оседают на внутренней стенке наружного цилиндра. Исследуя толщину осажденного слоя, можно оценить распределение молекул по скоростям, которое соответствует
максвелловскому распределению.
3. Опыт Ламмерта. Между источником молекулярного пучка и приемником синхронно вращаются два диска с
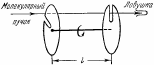 радиальными щелями.
радиальными щелями.
Из числа молекул, пролетевших через первую
щель, пролетят через второй диск только те, которые подлетят к нему в тот момент, когда на пути пучка встанет прорезь во втором диске. Изменяя угловую скорость вращения, можно исследовать распределение молекул по скоростям.
4. Опытное определение постоянной Авогадро:
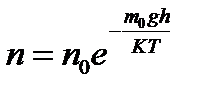 - концентрация на различных уровнях
- концентрация на различных уровнях
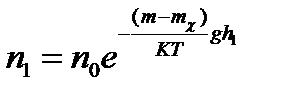
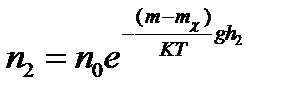
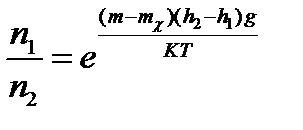
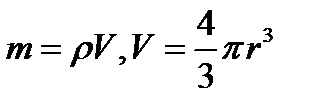
Тогда масса частицы равна
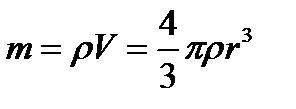
Тогда масса жидкости равна
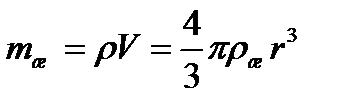
Следовательно,
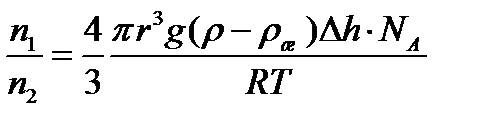
Число Авогадро