Связь поляризации и связанных зарядов.
Рассмотрим в однородном изотропном диэлектрике с неполярными молекулами воображаемую площадку S
Пусть в единице объема диэлектрика имеется n одинаковых частиц с зарядом +е и n одинаковых частиц с зарядом – е. Если поле в пределах диэлектрика однородно, то при включении поля все положительные заряды сместятся в направлении каком то там
Перенос отрицательного заряда в одном направлении эквивалентен переносу такого же по величине положительного заряда в противоположном направлении. Поэтому можно считать, что при включении поля через площадку S переносится в направлении вектора Р положительный заряд
Q=enSl1+enSl2=en(l1+l2)S
заряд, проходящий при включении поля через площадку S в направлении вектора Р, равен Q=PS
(15.4)
14. Поляризация и плотность связанных зарядов.
Рассмотрим внутри диэлектрика две воображаемые площадки S1 и S2, причем S1= S2=S. Площадки предполагаем перпендикулярными к Е и отстоящими друг от друга на Dx (рис. 31). До включения поля суммарный заряд, заключенный в цилиндрическом объеме с основанием S и высотой Dx, равен нулю.
При включении поля через площадку S1 входит внутрь цилиндра положительный заряд q1 = P1S (см. (15.4)), P1 – модуль вектора Р в сечении S1.
Одновременно через S2 выходит из цилиндра положительный заряд q2 == P2S (Р2 – модуль вектора Р в сечении S2). В результате в рассматриваемом объеме оказывается избыточный связанный положительный заряд
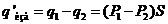 (15.5)
(15.5)
Если диэлектрик поляризован однородно (Р ≠ f(x,y,z)), то P1 = Р2 и избыточный связанный заряд 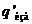 равен нулю. Однако, если диэлектрик поляризуется неоднородно, P1 ≠ Р2. Причинами неоднородной поляризации могут быть как неоднородности диэлектрика, так и неоднородности поля Е, связанные с присутствием свободных зарядов в месте неоднородности.
равен нулю. Однако, если диэлектрик поляризуется неоднородно, P1 ≠ Р2. Причинами неоднородной поляризации могут быть как неоднородности диэлектрика, так и неоднородности поля Е, связанные с присутствием свободных зарядов в месте неоднородности.
Пусть степень поляризации диэлектрика изменяется только в направлении оси х, совпадающей с направлением Е (рис. 31). Тогда P1 – Р2 представляет собой приращение DР, которое получает модуль вектора Р при смещении вдоль оси х на Dх. Поскольку DР ¹ 0, в объеме величиной SDx возникает избыточный заряд
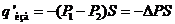
Разделив этот заряд на объем цилиндра SDx, получим объемную плотность связанных зарядов в сечении с координатой х (Dx полагаем малым):
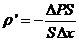
Устремив Dx к нулю, получим
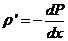 (15.6)
(15.6)
В общем случае, когда Р не совпадает по направлению с осью х и зависит не только от х, но и от координат y и z, для r' получается формула
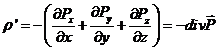 (15.7)
(15.7)
В случае Рх = Р, Рy = Рz =0 (15.6) есть частный случай (15.7).
Полученное соотношение оказывается справедливым и для диэлектриков с полярными молекулами.
Из выражения (15.5) для избыточного связанного заряда, заключенного в рассматриваемом объеме, вытекает еще одно важное соотношение. Найдем поток вектора Р через поверхность цилиндра, изображенного на рис. 31. Поток через боковую поверхность равен нулю, так как вектор Р касателен к этой поверхности. Нормальная составляющая Р для площадки S2 равна модулю вектора Р в сечении 2, т. е. Р2. Поэтому для потока через S2 получается значение P2S (S1 = S2 = S). Нормальная составляющая Р для площадки S1 равна –P1 (направления внешней нормали к S1 и вектора Р противоположны), так что соответствующий поток равен – P1S. Тогда, полный поток вектора Р через поверхность цилиндра равен
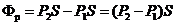
Сопоставив полученное нами выражение с правой частью формулы (15.5), приходим к соотношению между избыточным связанным зарядом, заключенным внутри цилиндра, и потоком вектора Р через поверхность цилиндра:
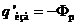 (15.8)
(15.8)
Избыточный заряд, заключенный в некотором объеме, равен алгебраической сумме находящихся в этом объеме связанных зарядов: 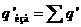 .
.
Поэтому (15.8) можно записать в виде
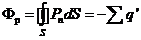 (15.9)
(15.9)
Можно доказать, что (15.9) справедлива для поверхности любой формы, при произвольной зависимости вектора Р от координат х, у, z, а также для полярных и неполярных диэлектриков.
Теперь выясним, что происходит на поверхности поляризованного диэлектрика. Пусть для начала внешняя плоская грань диэлектрика перпендикулярна к вектору Р (рис. 32,а). При включении поля все отрицательные заряды сместятся относительно положительных зарядов влево (против Р) на одинаковую величину l = l1+ l2 (рис. 30). В результате в поверхностном слое толщины l останутся только положительные заряды, дающие в сумме q’изб = enSl (на противоположной грани образуется такой же по величине отрицательный заряд). Разделив q’изб на S, получим поверхностную плотность связанного заряда: s’ = enl. Но eln есть модуль вектора поляризации Р, поэтому
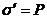 (15.10)
(15.10)
Перейдем к случаю, когда нормаль n к внешней плоской грани диэлектрика образует с вектором Р произвольный угол a (рис. 32,6). В этом случае объем косого цилиндра, равный
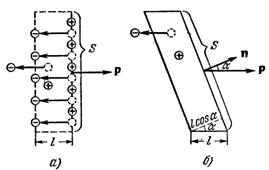 Рис. 32. Рис. 32. |
Slcosa свободен от отрицательных зарядов. Содержащийся в нем избыточный заряд равен 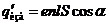 . Разделив этот заряд на S и учтя, что
. Разделив этот заряд на S и учтя, что 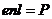 , получим
, получим
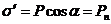 (15.11)
(15.11)
где Pn – проекция вектора Р на внешнюю нормаль к поверхности диэлектрика. При a = 0 проекция Pn равна Р, и мы приходим к формуле (15.10).
Формула (15.11) дает не только величину, но и знак поверхностного связанного заряда. В тех точках поверхности, где угол между внешней нормалью n и вектором Р острый, Pn > 0 и s’ положительна.. В тех точках, где n и Р образуют тупой угол, Pn < 0 и s ' отрицательна. Выразив согласно (15.2) Р через æ и Е, приходим к формуле
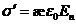 (15.12)
(15.12)
где En – нормальная составляющая напряженности поля внутри диэлектрика. В соответствии с (15.12) в тех местах, где линии напряженности выходят из диэлектрика (En > 0), на поверхности выступают положительные связанные заряды, там же, где линии напряженности входят в диэлектрик (En <0), появляются отрицательные поверхностные заряды.
Формулы (15.11) и (15.12) справедливы и в самом общем случае, когда неоднородный диэлектрик произвольной формы находится в неоднородном электрическом поле. Под Pn и En в этом случае нужно понимать нормальную составляющую соответствующего вектора, взятую в непосредственной близости к тому элементу поверхности, для которого определяется s’.
15. Описание поля в диэлектриках
Под напряженностью поля в диэлектрике понимают значение Е, получающееся усреднением истинного поля по физически бесконечно малому объему. Истинное (микроскопическое) поле в диэлектрике сильно меняется в пределах межмолекулярных расстояний. Однако при рассмотрении действия поля на макроскопические тела эти изменения сказываться не будут, и действие поля на тело определяется усредненным (макроскопическим) значением Е.
Макроскопическое поле Е получается в результате наложения двух полей: поля Е0, создаваемого свободными зарядами, которые могут передаваться от одного тела к другому при их касании, и поля Е' связанных зарядов. В силу принципа суперпозиции полей
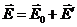 (16.1)
(16.1)
Поляризация диэлектрика обусловлена действием суммарного поля (16.1). Следовательно, именно это Е нужно подставлять в формулы (15.2) и (15.12).( P = æe0E; s’ = æ e0En)
Связанные заряды не могут покинуть пределы молекулы (или атома), в состав которой они входят. В остальном же их свойства таковы, как и у всех прочих зарядов. В частности, на связанных зарядах начинаются либо заканчиваются q'/e0 линий вектора Е'. Поэтому теорему Гаусса для определяемого выражением (16.1) вектора Е нужно записывать следующим образом:
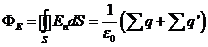 (16.2)
(16.2)
т. е. при вычислении потока вектора Е через замкнутую поверхность следует учитывать алгебраическую сумму не только свободных, но также и связанных зарядов, заключенных внутри поверхности. Поэтому формула (16.2) оказывается малопригодной для нахождения вектора Е в диэлектрике – она выражает свойства неизвестной величины Е через связанные заряды q', которые в свою очередь определяются неизвестной Е [см. (15.12)].
Затруднение, обусловленное тем, что Е зависит также и от связанных зарядов, можно обойти, введя в рассмотрение вспомогательную величину, связанную простым соотношением с вектором Е и определяемую лишь распределением в пространстве свободных зарядов. Чтобы установить вид этой вспомогательной величины, подставим в (16.2) выражение (15.9) ( 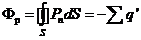 ), что позволит исключить из соотношений заряды q', заменив их потоком вектора Р.
), что позволит исключить из соотношений заряды q', заменив их потоком вектора Р.
После подстановки получим:
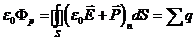 (16.3)
(16.3)
Выражение, стоящее в скобках под знаком интеграла, и есть та вспомогательная величина, о которой шла речь выше. Ее обозначают буквой D и называют электрическим смещением (или электрической индукцией).
Получаем
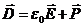 (16.4)
(16.4)
Теперь (16.3) может быть записана в виде
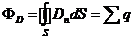 (16.5)
(16.5)
В случае непрерывного распределения свободных зарядов внутри поверхности с объемной плотностью r (16.5) видоизменяется:
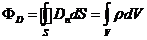 (16.6)
(16.6)
Формулы (16.5) и (16.6) выражают теорему Гаусса для вектора электрического смещения: поток вектора электрического смещения через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных зарядов.
В вакууме Р = 0, так что определяемая выражением (16.4) величина D превращается в e 0E и формулы (16.5) и (16.6) переходят в формулы (8.3) и (8.4).
Единицей потока вектора электрического смещения является кулон (K). Согласно (16.5) заряд в 1 К создает через охватывающую его поверхность поток смещения в 1 K.
Подставив в формулу (16.4) выражение (15.2 P = æe0E) для Р, получим
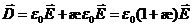 (16.7)
(16.7)
Безразмерную величину
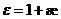 (16.8)
(16.8)
называют относительной диэлектрической проницаемостью или просто диэлектрической проницаемостью среды. Следовательно, соотношение (16.7) можно записать в виде
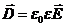 (16.9)
(16.9)
(В анизотропных диэлектриках направления D и Е, вообще говоря, не совпадают)
Это и есть то простое соотношение между векторами Е и D, о котором речь была выше. Согласно формулам (5.3) и (16.9) электрическое смещение поля точечного заряда в вакууме равно
 Рнс. 33. Рнс. 33. |
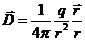 (16.10)
(16.10)
Единицей электрического смещения служит кулон на квадратный метр (к/м2).
Поле внутри плоской пластины.
Чтобы выяснить физический смысл величин D и e, рассмотрим пример поля в диэлектрике.
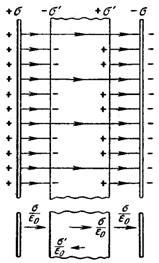
Рассмотрим поле, создаваемое в вакууме двумя бесконечными разноименно заряженными плоскостями. Обозначим напряженность поля Е0, а электрическое смещение D0 = e 0 Е0.
Внесем в это поле пластину из однородного диэлектрика и расположим ее так, как показано на рис. 33. Под действием поля на поверхностях диэлектрика появятся связанные заряды плотности s ’. Эти заряды создадут внутри пластины однородное поле, напряженность которого равна 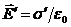 . Вне диэлектрика Е' = 0. Напряженность поля Е0 = s /e 0. Эти поля антипараллельны, тогда, внутри диэлектрика
. Вне диэлектрика Е' = 0. Напряженность поля Е0 = s /e 0. Эти поля антипараллельны, тогда, внутри диэлектрика
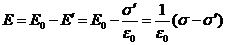 (16.17)
(16.17)
Вне диэлектрика Е = Е0.
Поляризация диэлектрика обусловлена полем (16.17). Поскольку оно перпендикулярно к поверхности пластины, Еn = Е. Кроме того, в соответствии с (15.12) 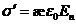 . Подставляя это значение в формулу (16.17), получаем
. Подставляя это значение в формулу (16.17), получаем 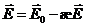 откуда
откуда
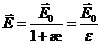 (16.18)
(16.18)
Итак, в рассматриваемом случае относительная диэлектрическая проницаемость e показывает, во сколько раз ослабляется поле за счет диэлектрика.
Умножив (16.18) на e0e, получим электрическое смещение внутри пластины
D = e0e E = e0E0. (16.19)
Таким образом, внутри пластины электрическое смещение равно напряженности поля свободных зарядов, умноженной на e0, т. е. совпадает с электрическим смещением внешнего поля D0. Вне пластины e = 1 и D также равно e0E0.
Чтобы найти s’, выразим в (16.17) Е и Е0 через плотности зарядов
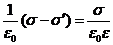
Отсюда
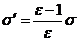 (16.20)
(16.20)
Таким образом, оказывается, что диэлектрическая проницаемость определяет относительную величину связанных зарядов по отношению к величине свободных зарядов, создающих электрическое поле.
Приведенный пример (рис.33) характерен тем, что диэлектрик был однородным и ограничивающие его поверхности совпадали с эквипотенциальными поверхностями. Полученный в этих случаях результат является общим. Если однородный диэлектрик полностью заполняет объем, ограниченный эквипотенциальными поверхностями, то вектор электрического смещения совпадает с вектором напряженности поля свободных зарядов, умноженным на e0 и, следовательно, напряженность поля внутри диэлектрика в ε раз меньше, чем напряженность поля свободных зарядов.
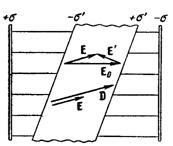 Рис. 35. Рис. 35. | 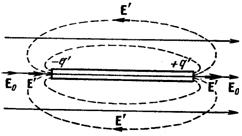 Рис. 36. Рис. 36. |
Если упомянутые условия не соблюдаются, векторы D и e0Е0 не совпадают. На рис. 35 показано поле в пластине диэлектрика, перекошенной относительно плоскостей, несущих свободные заряды. Вектор Е' перпендикулярен к граням пластины, поэтому Е и Е0 неколлинеарны. Вектор D направлен так же, как Е, следовательно, D и e0Е0 не совпадают по направлению. Можно показать, что они не совпадают и по величине.
Во всех рассмотренных выше примерах из-за специально выбранной формы диэлектрика поле Е' было отлично от нуля только внутри диэлектрика. В общем случае Е' может быть отлично от нуля и за пределами диэлектрика. Поместим в первоначально однородное поле стержень из диэлектрика (рис. 36). Вследствие поляризации на концах стержня образуются связанные заряды противоположных знаков. Их поле вне стержня эквивалентно полю диполя (линии Е' показаны на рисунке пунктиром). Легко видеть, что результирующее поле Е вблизи концов стержня больше Е0.
Преломление линий электрического смещения.
Поле вектора D можно изобразить с помощью линий электрического смещения (для краткости линий смещения), направление и густота которых определяются точно так же, как и для линий вектора Е.
Поместим в однородное поле Е0 две сложенные вместе плоскопараллельные однородные пластины из разных диэлектриков (рис. 37). При разных e1 и e2 плотности зарядов s '1 и s '2 также будут различными. Следовательно, на поверхности, по которой соприкасаются
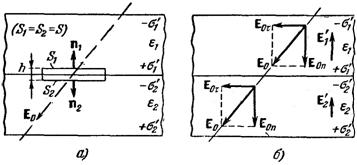 Рис. 37. Рис. 37. |
пластины, возникнет избыточный связанный заряд q'изб. Однако, как мы знаем, линии вектора D могут начинаться и заканчиваться только на свободных зарядах. Поэтому линии смещения пройдут через поверхность раздела двух диэлектриков, не прерываясь. Они лишь, как мы покажем ниже, претерпевают на этой поверхности излом.
Найдем соотношения между нормальными, а также между тангенциальными (по отношению к поверхности раздела) составляющими векторов D и Е в первом и во втором диэлектриках.
Рассмотрим воображаемый цилиндр высоты h, основания которого S1 и S2 расположены по разные стороны поверхности раздела (рис. 37,а). Применим к этому цилиндру теорему Гаусса. Внутри цилиндра имеются лишь связанные заряды, свободных зарядов по предположению там нет. Поэтому правая часть в формуле (16.5 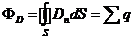 ) обращается в нуль. Потоком D через боковую поверхность цилиндра можно пренебречь, так как h мы устремим к нулю. Поток через верхнее основание цилиндра равен DlnS1, где Dln – нормальная составляющая вектора D в первом диэлектрике в непосредственной близости к поверхности раздела. Аналогично поток через нижнее основание есть D2nS2, где D2n – нормальная составляющая вектора D во втором диэлектрике также в непосредственной близости к поверхности раздела диэлектриков. Сложив эти два потока, мы получим полный поток, который по условию должен быть равен нулю:
) обращается в нуль. Потоком D через боковую поверхность цилиндра можно пренебречь, так как h мы устремим к нулю. Поток через верхнее основание цилиндра равен DlnS1, где Dln – нормальная составляющая вектора D в первом диэлектрике в непосредственной близости к поверхности раздела. Аналогично поток через нижнее основание есть D2nS2, где D2n – нормальная составляющая вектора D во втором диэлектрике также в непосредственной близости к поверхности раздела диэлектриков. Сложив эти два потока, мы получим полный поток, который по условию должен быть равен нулю:
ФD = DlnS1 + D2nS2 = (Dln + D2n) S = 0.
Отсюда следует, что Dln = – D2n. Знаки составляющих оказались различными вследствие того, что нормали n1 и n2 к основаниям цилиндра имеют противоположные направления. Если проектировать Dln и D2n на одну и ту же нормаль, то получится, что
Dln = D2n (17.1)
Заменив согласно (16.9 D = e 0 e Е) составляющие D соответствующими составляющими вектора Е, умноженными на e0e, получим соотношение
e0e1Еln = e0e2Е2n
из которого следует, что
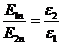 (17.2)
(17.2)
Теперь обратимся к тангенциальным составляющим векторов Е и D. Согласно формуле (16.1) Е = Е0 + Е'.
Вектор Е0 в обоих диэлектриках по предположению одинаков. Векторы Е', как видно из рис. 37, б, направлены по нормали к поверхности раздела, вследствие чего оказывают влияние только на нормальные составляющие вектора Е. Отсюда заключаем, что тангенциальные составляющие вектора Е в обоих диэлектриках должны быть одинаковыми:
Е1t = Е2t (17.3)
Заменив согласно (16.9 D = e 0 e Е) составляющие Е соответствующими составляющими вектора D, деленными на e0e, получим соотношение
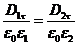
из которого следует, что
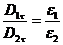 (17.4)
(17.4)
Резюмируя, можно сказать, что при переходе через границу раздела двух диэлектриков нормальная составляющая вектора D и тангенциальная составляющая вектора Е изменяются непрерывно. Тангенциальная же составляющая вектора D и нормальная составляющая вектора Е при переходе через границу раздела претерпевают разрыв.
