Внутренняя энергия системы. Первое начало термодинамики. Элементарное количество теплоты и работы.

Масса и размеры молекул

Атомным весом (А) химического элемента называется отношение массы атома этого элемента к 1/12 массы атома С. Молекулярным весом (М) вещества называется отношение массы молекулы этого вещества к 1/12 массы атома С¹².атомный и молекулярный веса – безразмерные величины.

Единица массы, равная 1/12 массы атома С, сокращенно обозначается русской аббревиатурой «ед» Поэтому величина этой единицы, выраженная в килограммах, обозначается какm ед. Тогда масса атома, выраженная в килограммах, равна A× m ед, а масса молекулы М× m ед.

Понятно, что два химически простых вещества, взятых в таких количествах, что их массы m₁ и m₂ относятся как атомные веса А₁ и A₂, будут содержать по одинаковому числу атомов. Такое количество данного элемента, масса которого, выраженная в килограммах, численно равна его атомному весу, называют килограмм – атомом. Такое количество данного вещества, масса которого, выраженная в килограммах, численно равна его молекулярному весу, называется килограмм-молекулой или кратко киломолем (обозначается кмоль).

Масса киломоля( буква мю) численно равна молекулярному весу М. Это служит причиной того, что m иногда называют молекулярным весом. Однако следует иметь в виду, что, в то время как М – величина безразмерная, масса киломоля m имеет размерность кг/кмоль. Поскольку массы килограмм-молекул относятся как соответствующие молекулярные веса, киломоли всех веществ содержат одно и то же число молекул,

Число N_A называется числом Авогадро. N_A = 6,023×10²⁶ кмоль^-1.

Теперь можно оценить размеров атомов. Естественно предположить, что в твердых телах атомы располагаются довольно близко друг к другу. Поэтому приближенную оценку объема одного атома можно получить, разделив объем киломоля кристалла, например железа, на число атомов в киломоле N_A.

Состояние системы. Процесс.

Системой тел или просто системой называется совокупность рассматриваемых тел.

Всякая система может находиться в различных состояниях, отличающихся температурой, давлением, объемом и т. д. Подобные величины, характеризующие состояние системы, называются параметрами состояний.

Равновесие. Неравновесие.

Всякий процесс, т. е. переход системы из одного состояния в другое, связан с нарушением равновесия системы. Процесс, состоящий из непрерывной последовательности равновесных состояний, называется равновесным. Из сказанного следует, что равновесным может быть только бесконечно медленный процесс, поэтому равновесный процесс является абстракцией.

Понятия равновесного состояния и равновесного процесса играют большую роль в термодинамике. Все количественные выводы термодинамики строго применимы только к равновесным процессам.

Температура. Измерение температуры.

От температуры зависит ряд свойств тел – объем, электрическое сопротивление и т. п. Любое из этих свойств может быть использовано для количественного определения температуры.

Выражение температуры через объем для термометра: t=(V-V0/V100-V0)*100

Установленная таким образом температурная шкала называется, как известно, шкалой Цельсия. Проградуировав описанным способом термометр, его можно использовать для измерения температуры, приводя в тепловое равновесие с тем телом, температура которого нас интересует, и, производя отсчет величины объема.

Уравнение состояния идеального газа. Абсолютная температура.

Соотношение, дающее связь между параметрами какого-либо тела, называется уравнением состояния этого тела.

закон Бойля – Мариотта :pV = const (t° = const).

Закон Гей-Люссака: V= V₀(l+ at°) (p = const).

+ кривые изопроцессов!

Абсолуютная температура ( Кельвины) = с+273

Из этих уравнений следует газовый закон ( объединенный БМ и ГЛ)

V1/V2=T1/T2( p const) P1/P2=T1/T2(v const)

И тогда p1V1/T1=p2V2/T2

,

Это уравнение называют уравнением Клапейрона. Оно связывает параметры киломоля идеального газа и, следовательно, представляет собой уравнение состояния идеального газа. Его обычно пишут в виде

pV_км = RT

R- газовая постоянная.

От уравнения для одного киломоля легко перейти к уравнению для любой массы газа m, получаем:

pV_км = (мю/М)RT

Это и есть уравнение состояния идеального газа, написанное для произвольной массы газа m

Идеальный газ во внешнем поле.

ЗАГУГЛИ(первая ссыль)

Распределение Максвелла

Тепловая скорость представляет собой некоторую среднюю характеристику теплового движения частиц. В действительности различные молекулы движутся с различными скоростями и можно поставить вопрос о распределении молекул по скоростям: сколько (в среднем) из имеющихся в теле молекул обладает теми или иными скоростями?

ШПОРА

Политропические процессы

Все рассмотренные ранее процессы являются частными случаями политропического процесса.

pV^n=const

n=0 Изобара

n=1 Изотерма

n=y Адиабат

n=+- беск Изохора

Цикл Карно

Работу можно произвести только с помощью системы тел, не находящихся в тепловом равновесии друг с другом.

Пусть существует система, состоящая их двух тел с различной температурой.

.

Следующие стадии предлагаемого процесса. Рабочее тело отсоединено от нагревателя, теплоизолировано и подвергнуто дальнейшему расширению, на этот раз адиабатическому. При этом газ охлаждается, а расширение продолжается до тех пор, пока температура газа не упадет до температуры охладителя Т₁. Этот процесс изображается на диаграмме адиабатой ВС, более крутой, чем изотерма АВ, поскольку при адиабатическом расширении давление падает быстрее, чем при изотермическом расширении.

Далее рабочее тело приведено в соприкосновение с охладителем и газ изотермически (при температуре Т₁) сжат, причем он отдает некоторое количество тепла охладителю.

Последняя стадия – отсоединение рабочего тела от охладителя и его адиабатическое сжатие. В результате тело возвращается в исходное состояние. Для этого надо должным образом подобрать точку D, т. е. объем, до которого доводится изотермическое сжатие CD.

Таким образом, рабочее тело испытало круговой процесс, возвратившись в исходное состояние, но произведя при этом определенную работу, изображающуюся площадью криволинейного четырехугольника ABCD. Совершение этой работы произошло за счет того, что на верхней изотерме рабочее тело отняло у нагревателя большее количество тепла, чем оно отдало охладителю на нижний изотерме. Все этапы этого кругового процесса обратимы и потому произведенная работа – максимальная возможная (при заданной затрате тепла нагревателем).

Описанный процесс называется циклом Карно. Он показывает, что, в принципе, при наличии двух тел с различной температурой можно совершить работу обратимым образом. Будучи максимально возможной, эта работа не зависит от свойств вспомогательного рабочего тела.

КПД.

ШПОРА

Природа необратимости

состояние равновесия, в котором макроскопическое движение отсутствует, может осуществиться неизмеримо большим числом способов, чем состояние, в котором значительная энергия сконцентрирована в виде кинетической энергии упорядоченного движения – движения тела как целого.

Таким образом, переход из неравновесного состояния в равновесное представляет собой переход из состояния, которое может осуществиться меньшим числом способов, в состояние, которое может осуществиться большим числом способов. Ясно, что наиболее вероятным будет то состояние тела (или системы тел), которое может осуществиться наибольшим числом способов,– это и будет состояние теплового равновесия. Поэтому, если предоставленная самой себе (т. е. замкнутая) система в некоторый момент времени не находится в состоянии равновесия, то в последующее время подавляюще вероятным будет переход ее в состояние, которое может осуществиться несравненно большим числом способов, т. е. приближение к равновесию.

Наоборот, после того как замкнутая система пришла в состояние равновесия, подавляюще маловероятным был бы самопроизвольный выход системы из этого состояния.

Таким образом, необратимость тепловых процессов имеет вероятностный характер.

Количественной характеристикой теплового состояния тела, описывающей его стремление переходить в другие состояния, является число микроскопических способов, которым это состояние может быть осуществлено. Это число называют статистическим весом состояния; обозначим его буквой Г. Тело, предоставленное самому себе, стремится перейти в состояние с большим статистическим весом. Принято, однако, пользоваться не самим числом Г, а его логарифмом, который еще умножают на постоянную Больцмана k.

Определенную таким образом величину S = klnГ называют энтропией тела.

dS=dQ/T

S=S1+S2- энтропия системы

Неравновесные процессы.

процессы, с помощью которых происходит установление состояния равновесия. Такие процессы называют кинетическими. Формальная сторона вопроса станет ясной при рассмотрении конкретных процессов. Наконец, следует отметить, что по своей сути все эти процессы, как приближающие тело к состоянию равновесия, являются необратимыми.

Диффузия.

Если концентрация какого-либо раствора различна в разных его местах, то благодаря тепловому движению молекул он с течением времени перемешивается: растворенное вещество переходит из мест с большей в места с меньшей концентрацией до тех пор, пока состав раствора не станет одинаковым по всему его объему. Этот процесс называется диффузией.

Пусть для простоты концентрация раствора c меняется только вдоль одного направления, соответствующего оси х. Количество растворенного вещества, переходящее в единицу времени через перпендикулярную оси х поверхность единичной площади, обычно называется диффузионным потоком j.

Пусть j – число молекул растворенного вещества, проходящего в 1 сек через 1 м². Тогда [j] = 1/сек×м². Концентрация же есть число растворенных молекул в 1 м³ и ее размерность [с]= = 1/ м^-3. Сравнение размерности с обеих сторон равенства j = – Ddc/dx,

Процесс диффузии подразумевает, что она происходит в покоящейся среде, так что выравнивание концентрации происходит исключительно благодаря неупорядоченному тепловому движению отдельных молекул. Предполагается, что жидкость (или газ) не перемешивается никакими внешними воздействиями, приводящими ее в движение.

Теплопроводность.

Диффузии родственен процесс теплопроводности. Если в разных местах тела температура различна, то возникает поток тепла из мест более нагретых в места менее нагретые, продолжающийся до тех пор, пока температура во всем теле не выровняется. И здесь механизм процесса связан с беспорядочным тепловым движением молекул: молекулы из более нагретых мест тела, сталкиваясь при своем движении с молекулами соседних, менее нагретых участков, передают им часть своей энергии.

Как и при рассмотрении диффузии подразумевается, что теплопроводность происходит в покоящейся среде. В частности, предполагается, что в среде отсутствуют какие-либо перепады давления, которые приводили бы к возникновению движения в ней.

Коэффициент теплопроводности определяет скорость передачи тепла от более нагретых к менее нагретым участкам.

Обращает на себя внимание очень большая теплопроводность металлов. Причина этого заключается в том, что в металлах, в отличие от других тел, тепло переносится тепловым движением не атомов, а свободных электронов. Большая эффективность электронной теплопроводности связана со скоростями электронов, порядка 10⁶ м/сек, т. е. гораздо большими, чем обычные тепловые скорости атомов и молекул (10² – 10³ м/сек).

ЭЛЕКТРИЧЕСТВО.

Теорема Гаусса

Окружающую точечный заряд q сферическую поверхность любого радиуса r пересекает 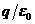линий Е. То есть, из точечного заряда выходит (либо к нему сходится) 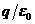линий. В соответствии с (9) поток вектора Е через некоторую поверхность численно равен количеству линий Е, пересекающих эту поверхность. Следовательно, поток вектора Е через охватывающую заряд сферическую поверхность равен 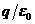. Знак потока совпадает со знаком заряда.

Независимость потока от поверхности. Поток вектора Е равен 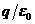для поверхности любой другой формы, если она замкнута и заключает внутри себя точечный заряд q,. Для поверхности, не имеющей «морщин» (рис. 10,а), это утверждение очевидно. Действительно, такая поверхность, как и поверхность сферы, пересекается каждой линией Е только один раз.

Поэтому число пересечений равно количеству линий, выходящих из заряда, т. е. 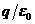. При вычислении потока через поверхность с «морщинами» (на рис. 10,6 показана только одна из 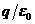линий Е) нужно учесть, что число пересечений данной линии с поверхностью может быть в рассматриваемом случае только нечетным, причем эти пересечения будут вносить в общий поток попеременно то положительный, то отрицательный вклад. То есть, сколько бы раз данная линия не пересекала поверхность, результирующий вклад в поток будет равен либо плюс единице (для линии, выходящей в конечном счете наружу), либо минус единице (для линии, входящей внутрь). Таким образом, какова бы ни была форма замкнутой поверхности, охватывающей точечный заряд q, поток вектора Е сквозь эту поверхность оказывается равным .

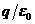Пусть внутри некоторой замкнутой поверхности заключено несколько точечных зарядов произвольных знаков: q₁, q₂ и т. д. Поток вектора Е по определению равен

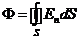(12)

(кружок у знака интеграла указывает на то, что интегрирование производится по замкнутой поверхности). В силу принципа суперпозиции полей

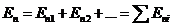(13)

Подстановка (13) в выражение для потока дает

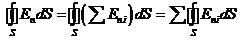
где 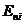– нормальная составляющая напряженности поля, создаваемого i-м зарядом в отдельности. Последняя перестановка операции суммирования и интегрирования возможна, так как i относится к нумерации зарядов, интегрирование ведется по произвольной поверхности.

Выше было показано:

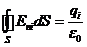
Следовательно,

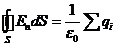(14)

Это утверждение носит название теоремы Гаусса. Теорема может быть сформулирована следующим образом: поток вектора напряженности электрического поля через замкнутую

Рис. 11.

поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на e ₀.

В частности. Если внутри поверхности заряды отсутствуют, поток равен нулю. В этом случае напряженность поля создавается зарядами, расположенными вне поверхности. Каждая линия напряженности пересекает поверхность четное число раз, выходя наружу столько же раз, сколько и входя внутрь (рис. 11). В итоге вклад, вносимый в поток каждой из линий, будет равен нулю. Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью r, теорема Гаусса должна быть записана следующим образом:

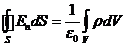(15)

где интеграл справа берется по объему V, охватываемому поверхностью S.

6. Напряженность для различных конфигураций источников поля.

В случае удачной симметрии распределения зарядов теорема Гаусса позволяет найти напряженность поля гораздо проще, чем с использованием формулы для напряженности поля точечного заряда и принципа суперпозиции полей.

Определения.

Объемная плотность заряда аналогична обычной плотности: p=lim(dq/dV)

где dq – заряд, заключенный внутри малого объема dV.

Поверхностная плотность заряда: сигма=lim(dq/dS)

где Dq – заряд, находящийся на отрезке цилиндрического тела, имеющем длину Dl

Пользуясь теоремой Гаусса можно получить значения напряженностей для ряда часто используемых случаев распределения зарядов.

1. Поле бесконечной однородно заряженной плоскости.Плоскость заряжена с постоянной поверхностной плотностью (сигма). Из соображений симметрии следует, что Е в любой точке поля перпендикулярна к плоскости. В самом деле, поскольку плоскость бесконечна и заряжена однородно (т. е. с постоянной плотностью), нет никаких оснований к тому, чтобы сила, действующая на пробный заряд, отклонялась в какую-либо сторону от

нормали к плоскости.

Очевидно также, что в симметричных относительно плоскости точках Е одинакова по величине и противоположна по направлению.

откуда E=сигма/2(e0)

Таким образом, на любом расстоянии от плоскости напряженность одинакова по величине.

2. Поле двух разноименно заряженных плоскостей.

Поле двух параллельных бесконечных плоскостей, заряженных разноименно с одинаковой поверхностной плотностью сигма, определяется суперпозицией полей, создаваемых каждой из плоскостей в отдельности. В области между плоскостями (рис. 15) складываемые поля имеют одинаковое направление, так что результирующая напряженность равна E=сигма/e0

Вне объема, ограниченного плоскостями, складываемые поля имеют противоположные направления, так что результирующая напряженность равна нулю.

3. Поле бесконечного заряженного цилиндра.

Имеется бесконечная цилиндрическая поверхность радиуса R, заряженная с постоянной поверхностной плотностью сигма. Симметрия задачи подсказывает, что напряженность поля в любой точке направлена перпендикулярно к оси цилиндра, а величина напряженности определяется только расстоянием r от оси цилиндра. При этом на одинаковых расстояниях от центра цилиндра напряженность одинакова. E=сигма/e0

4. Поле заряженной сферической поверхности. Поле сферической поверхности радиуса R, заряженной с постоянной поверхностной плотностью s, очевидно, характеризуется центральной симметрией. То есть направление вектора Е в любой точке проходит через центр сферы, а величина напряженности является функцией только расстояния r от центра сферы.

E=сигма/e0

5. Поле объемно заряженной сферы радиуса R, заряженной с постоянной объемной плотностью r. Как и в предыдущем случае, поле такой сферы обладает центральной симметрией. Понятно, что для поля вне сферы получается тот же результат [в том числе и формула (17)]. Однако для точек внутри сферы результат будет иным. Сферическая поверхность радиуса r < R заключает в себе заряд,

E=(1/4pi(e0))*(q/R^3)*(r)

Таким образом, внутри сферы напряженность поля растет линейно с расстоянием r от центра сферы. Вне сферы напряженность убывает по такому же закону, как и у поля точечного заряда.

7. Работа сил электростатического поля

Сила, действующая на точечный заряд, находящийся в поле другого неподвижного точечного заряда, является центральной. Из механики известно, что центральное поле сил потенциально. То есть, работа действительно зависит лишь от начального и конечного положений этого заряда (от r₁ и r₂) и не зависит от траектории перемещения заряда q'. Следовательно, силы, действующие на заряд q' в поле неподвижного заряда q, потенциальны.

Этот вывод распространяется на поле любой системы неподвижных зарядов. Сила 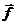, действующая на точечный заряд q', по принципу суперпозиции равна

F=суммFi

где 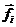– сила, обусловленная i-м зарядом системы источников поля. Работа равна сумме работ, совершаемых отдельными силами:

A=суммAi

Каждое из слагаемых не зависит от пути. Следовательно, не зависит от пути и работа A.

Еще можно сказать о циркуляции и о том что циркуляция равна нуля в потенц поле

8. Потенциал

Тело, находящееся в потенциальном поле сил, обладает потенциальной энергией, за счет которой совершается работа силами поля.

Следовательно, работа (9.1) равна разности значений потенциальной энергии, которыми обладал заряд q' в точках 1 и 2 поля заряда q:

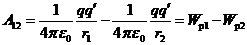
Отсюда выражение для потенциальной энергии заряда q' в поле заряда q

W=(1/4pi(e0))(qq/r)+C

Значение постоянной С выбирается таким, чтобы при удалении заряда на бесконечность (r = ¥) потенциальная энергия обращалась в нуль.

Величина фи=W/q

называется потенциалом поля в данной точке и является энергетической характеристикой электрического поля.

Потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд. Следовательно потенциал поля точечного заряда равен: фи=(1/4pi(e0))(q/r)

Потенциал поля, создаваемого системой зарядов, равен сумме потенциалов, создаваемых каждым из зарядов в отдельности.

потенциальная энергия заряда q, находящегося в точке поля с потенциалом фи

W=qфи

Таким образом, работа, совершаемая над зарядом силами поля, равна произведению величины заряда на разность потенциалов в начальной и конечной точках.

А=qфи

9. Связь между напряженностью электрического поля и потенциалом

Электрическое поле можно описать либо с помощью векторной величины Е, либо с помощью скалярной величины фи. Между этими величинами должна существовать связь. Так как Е пропорциональна силе, действующей на заряд, а фи – потенциальной энергии заряда, понятно, что эта связь должна быть аналогична связи между потенциальной энергией и силой.

Используя обозначение градиента, можно написать E = – gradфи

Напряженность электрического поля равна градиенту потенциала, взятому с обратным знаком.

Соотношение между напряженностью поля и потенциалом точечного заряда. Потенциал этого поля равен

Фи=

Проекция gradj на направление r равна

gradфи =(-1/4pi(e0))(q/r^2)

Разность потенциалов между двумя бесконечными разноименно заряженными плоскостями (однородное поле).

Фи1-фи2= E*d d-расстояние между пластинами конденастора

В частности, это выражение определяет связь разности потенциалов между пластинами конденсатора с напряженностью поля в конденсаторе. Расстояние между пластинами равно d.

Поле диполя.

Потенциал поля электрического диполя.

Посмотреть по Иродову. Электрический диполь – система двух одинаковых по величине разноименных точечных зарядов: +q и –q. Расстояние между ними значительно меньше, чем расстояние до тех точек, в которых определяется поле системы. Прямая, проходящая через оба заряда, называется осью диполя. Задача: найти напряженность поля на оси диполя, а также на прямой, проходящей через центр диполя и перпендикулярной к его оси (рис. 4).

Положение точек на этих прямых определим их расстоянием r от центра диполя.

Таким образом, Е_ll = 2 Е_^. В общем случае рассмотрения напряженность поля диполя в произвольной точке определяется формулой

E=(1/4pi(e0)(p/r^3)(кор(1+3cos^2a)

где a – угол между осью диполя и направлением на данную

МАГНЕТИЗМ.

МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ.

Магнитное поле

Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения[1], магнитная составляющая электромагнитного поля[2]

Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты).

Кроме этого, оно появляется при наличии изменяющегося во времени электрического поля.

Основной силовой характеристикой магнитного поля является вектор магнитной индукции B (вектор индукции магнитного поля). С математической точки зрения B — векторное поле Нередко вектор магнитной индукции называется для краткости просто магнитным полем (хотя, наверное, это не самое строгое употребление термина).

магнитным моментом контура Pm=IS

магнитная индукция B=M(вращ мом)/Pm

Сила Лоренца

Проводник, по которому течет ток, отличается от проводника без тока лишь тем, что в нем происходит упорядоченное движение носителей заряда. Отсюда напрашивается вывод, что сила, действующая на проводник с током в магнитном поле, обусловлена действием сил на отдельные движущиеся заряды, а уже от этих зарядов действие передается проводнику, по которому они перемещаются. Этот вывод подтверждается целым рядом опытных фактов и, в частности, тем, что пучок свободно летящих заряженных частиц, например электронный пучок, отклоняется магнитным полем.

Сила Лоренца — сила, с которой, в рамках классической физики, электромагнитное поле действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью v заряд q лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще[1], иначе говоря, со стороны электрического E имагнитного

B полей. Выражается в СИ как: F=q(E+(v x B))

МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ

Магнитное поле в веществе

Экспериментальные исследования показали, что все вещества в большей или меньшей степени обладают магнитными свойствами. Если два витка с токами поместить в какую-либо среду, то сила магнитного взаимодействия между токами изменяется. Этот опыт показывает, что индукция магнитного поля, создаваемого электрическими токами в веществе, отличается от индукции магнитного поля, создаваемого теми же токами в вакууме

Магнитные свойства веществ определяются магнитными свойствами атомов или элементарных частиц (электронов, протонов и нейтронов), входящих в состав атомов.

Одним из важнейших свойств электрона является наличие у него не только электрического, но и собственного магнитного поля. Собственное магнитное поле электрона называют спиновым

Физическая величина, показывающая, во сколько раз индукция B магнитного поля в однородной среде отличается по модулю от индукции B0 магнитного поля в вакууме, называется магнитной проницаемостью: ебнутая буква=B0/B

Намагни́ченность— векторная физическая величина, характеризующая магнитное состояние макроскопического физического тела. Обозначается обычно М или J. Определяется как магнитный моментединицы объёма вещества:

M=m/V

Здесь, M — вектор намагниченности; m - вектор магнитного момента; V — объём.

Магнитная восприимчивость — физическая величина, характеризующая связь между магнитным моментом (намагниченностью) вещества и магнитным полем в этом веществе.

В общем связь соотношение между магнитной индукцией и напряженностью магнитного поля через магнитную проницаемость вводится как B=ебанутая буква* H

МАГНЕТИКИ

Классификация магнетиков

Прежде чем изложить классификацию магнетиков, рассмотрим величины, с помощью которых принято характеризовать магнитные свойства разных веществ. В § 44 была введена для этой цели восприимчивость c, определяющая величину намагничения единицы объема вещества

Часто вместо восприимчивости единицы объема c пользуются отнесенной к одному киломолю вещества киломолярной (для химически простых веществ – килоатомной) восприимчивостью c_км (c_кат) или отнесенной к единице массы удельной восприимчивостью c_уд. Между значениями этих восприимчивостей имеются соотношения: c_км = cV_км где V_км – объем киломоля вещества (в м³/кмоль), c_уд = (1/d)c, где d – плотность вещества (в кг/м³). В то время как c – безразмерная величина, c_км (или c_кат) имеет размерность м³/кмоль (или м³/кат), а c_уд – м³/кг.

Восприимчивость, отнесенная к молю (грамм-молекуле) вещества, называется молярной (для химически простых веществ – атомной). Очевидно, что c_м = cV_м, где V_м – объем моля вещества (в см³/моль).

В зависимости от знака и величины магнитной восприимчивости все магнетики подразделяются на три группы:

1) диамагнетики, у которых c отрицательна и мала (c_км ~ 10^–8 – 10^–7 м³/кмоль);

2) парамагнетики, у которых c невелика, но положительна (c_км ~ 10^–7 – 10^–6 м³/кмоль);

3) ферромагнетики, у которых c положительна и достигает очень больших значений (c_км ~ 10³ м³/кмоль).

Кроме того, в отличие от диа- и парамагнетиков, для которых c постоянна, магнитная восприимчивость ферромагнетиков является функцией напряженности магнитного поля. Таким образом, вектор намагничения J может как совпадать по направлению с Н (у пара- и ферромагнетиков), так и быть направленным в противоположную сторону (у диамагнетиков). Напомним, что у диэлектриков вектор поляризации всегда направлен в ту же сторону, что и Е.

Диамагнетизм

Диамагнетизм — один из видов магнетизма, который проявляется в намагничивании вещества навстречу направлению действующего на него внешнего поля.

Диамагнетизм свойствен всем веществам. Диамагнетизм можно рассматривать как следствие индукционных токов, наводимых в заполненных электронных оболочках ионов внешним магнитным полем. Эти токи создают в каждом атоме индуцированный магнитный момент, направленный, согласно правилу Ленца, навстречу внешнему полю (независимо от того, имелся ли первоначально собственный момент или нет и как он был ориентирован). Диамагнетизм, однако, невозможно описать с позиции только классической физики, это суть предельно квантовомеханическое явление. [1] Идеальный диамагнетизм носит некооперативный характер и характеризуется отрицательной, не зависящей от температуры магнитной восприимчивостью. Диамагнетизм входит в состав любого магнитного состояния вещества, но он обычно пренебрежимо мал по сравнению с магнетизмом, обусловленным наличием спонтанных магнитных моментов в системе. У чисто диамагнитных веществ электронные оболочки (молекул) не обладают постоянным моментом. Моменты, создаваемые отдельными электронами в таких в отсутствие внешнего поля взаимно скомпенсированы. В частности, это имеет место в ионах и молекулах с целиком заполненными электронными оболочками, например в инертных газах, в молекулах.

Под действием вращательного момента М векторы L(механический момент) и p_m совершают прецессию вокруг направления вектора магнитной индукции В, скорость которой легко найти.

За время dt вектор L получает приращение dL, равное dL = Mdt

Вектор dL, как и вектор М, перпендикулярен к плоскости, проходящей через векторы В и L, и по модулю равен |dL| = p_m В sina dt,

где a – угол между p_m и В.

Итак, под действием внешнего магнитного поля происходит прецессия электронных орбит с одинаковой для всех электронов угловой скоростью (52.1). Обусловленное прецессией дополнительное движение электронов приводит к возникновению индуцированного магнитного момента атома (52.5), направленного против поля. Ларморова прецессия возникает у всех без исключения веществ. Однако в тех случаях, когда атомы обладают сами по себе магнитным моментом, магнитное поле не только индуцирует момент (52.5), но и оказывает на магнитные моменты атомов ориентирующее действие, устанавливая их по направлению поля. Возникающий при этом положительный (т. е. направленный вдоль поля) магнитный момент бывает значительно больше, чем отрицательный индуцированный момент. Поэтому результирующий момент оказывается положительным и вещество ведет себя как парамагнетик.

Диамагнетизм обнаруживают лишь те вещества, у которых атомы не обладают магнитным моментом (векторная сумма орбитальных и спиновых магнитных моментов электронов атома равна нулю). Если для.такого вещества умножить равенство (52.5) на число Авогадро N_A, получится магнитный момент килограмм-атома вещества. Разделив его на напряженность поля Н, найдем килограмм-атомную магнитную восприимчивость c_кат.

Парамагнетизм

Парамагнетики — вещества, которые намагничиваются во внешнем магнитном поле в направлении внешнего магнитного поля. Парамагнетики относятся к слабомагнитным веществам, магнитная проницаемость незначительно отличается от единицы

Если магнитный момент Pm атомов отличен от нуля, вещество оказывается парамагнитным. Внешнее магнитное поле стремится установить магнитные моменты атомов вдоль В, тепловое движение стремится разбросать их равномерно по всем направлениям. В результате устанавливается некоторая равновесная преимущественная ориентация моментов вдоль поля тем большая, чем больше В, и тем меньшая, чем выше температура.

Кюри экспериментально установил закон, согласно которому парамагнитная килограмм-атомная восприимчивость вещества равна

X=C/T

где С – постоянная Кюри, зависящая от рода вещества, Т – абсолютная температура.

Классическая теория парамагнетизма была развита Ланжевеном в 1905 г. Мы ограничимся изложением этой теории для случая не слишком сильных полей и не очень низких температур.

У парамагнетиков магнитная восприимчивость уменьшается с температурой, подчиняясьзакону Кюри — Вейса

. У ферромагнетиков магнитная восприимчивость с ростом температуры увеличивается, достигая резкого максимума вблизи точки Кюри

Ферромагнетизм.

Особый класс магнетиков образуют вещества, способные обладать намагничением даже в отсутствие внешнего магнитного поля. По своему наиболее распространенному представителю – железу – они получили название ферромагнетиков. К их числу принадлежат железо, никель, кобальт, гадолиний, их сплавы и соединения Ферромагнетизм присущ всем этим веществам только в кристаллическом состоянии.

Ферромагнетики являются сильномагнитными веществами– их намагничение в огромное (до 10¹⁰) число раз превосходит намагничение диа- и парамагнетиков, принадлежащих к категории слабомагнитных веществ.

Намагничение слабомагнитных веществ изменяется с напряженностью поля линейно. Намагничение ферромагнетиков зависит от Н сложным образом

Свойства ферромагнетиков

Магнитная восприимчивость ферромагнетиков положительна и значительно больше единицы.

При не слишком высоких температурах ферромагнетики обладают самопроизвольной (спонтанной) намагниченностью, которая сильно изменяется под