Явление самоиндукции. Инд-ность. ЭДС самоинд.

Возникновение инд-го тока в контуре при изм-ии магн. п., вызванного изменением тока, текущего через контур. Поток, пронизывающий контур с током пропорционален току Ф = L·I, где L – индуктивность, кот. зависит от размеров и геометрии контура, а также от магн. проницаемости среды. Тогда ЭДС = – dФ /dt = –d(LI) /dt = –(LdI /dt + IdL /dt). При L=const ЭДС = –LdI /dt

Ток при замыкании и размыкании цепи.

Если ключ замкнут, в цепи течет ток I₀ = ε /R. При размыкании ток начинает убывать, появл. сомоинд., препядств. убыванию тока. ε_с= –LdI /dt. или ε_с=IR. Прировняв и решив диф. ур-е получим I = C·e^(-t·R/L) {C=I₀,τ =L/R, t=τ } I= I₀/e

После замыкания ток начнет возрастать до опред. значения, при этом присутствует ε_с. IR = ε – LdI /dt. Реш. ур. получим I =I₀ +C·e^(-t/τ) = I₀(1 – e^(-t/τ))

Энергия магн. п.

Работа, совершаемая током, прох. через катушку при замык. цепи: dA=–IdФ=–I·LdI => A =1/2·LI² .=> W=1/2·LI²=1/2μμ₀n²V· (H/n)²=1/2μμ₀V·H². Плотность м.п.: w = W/V=1/2μμ₀·H²=B² / 2μμ₀

Свободные электромагн. колебания.

Колебания, кот. возникают в идеальном колеб. контуре, т.е. конт., состоящий из ёмкости, индуктивности и сопротивления. В к.к. происходит попеременная разрядка и зарядка конденсатора и катушки. Wэл+Wм=0 => q² /2C + LI² /2 =0. Ур-ия колебаний: d²q/dt² + ω₀²q =0. период T=2π(√LC). макс ток I_max=q_max ω₀ .

Затухающие электромаг. колебания.

Контур затухает из-за присутств. R, т.е. энергия тратиться на нагревание. Ур-ние колебаний: d²q /dt² +2βdq /dt + ω₀²q =0 ,где ω₀² =1/LC, 2β =R/L.Реш.: q=q_maxe^-βtcos(ω₀t+φ)

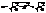
Вынужденные электром. колебания.

Колеб. контур с источником переменного ЭДС. Ур-ние колебания: d²q /dt² +2βdq /dt + ω₀²q = U_maxcos(ωt)., гле ω₀² =1/LC, 2β =R/L. Тогда з-н Ома для данной цепи:

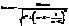
Вихревое электрическое поле.

Максвелл предположил, что явление ЭДС изменяющегося м.п. порождает вихревое электрическое поле. Изменение магнитного поля порождает электрическое. Это поле является вихревым, а линии поля должны быть замкнуты. rotE‾= –dB‾ /dt

Ток смещения.

Перемен. эл. п., так же как и эл. ток, является источником магн.п. Колич. мерой магнитного действия переменного эл. п. служит ток смещения: j‾_см = dD‾ /dt, где D‾= εE‾+P‾ – в-р эл. смещения ((P‾-в-р поляризованности)). Током смещения сквозь пов-ть S наз. физ. велич., равная потоку j‾_см сквозь эту пов-ть: Iсм =∫[S] j‾_см dS‾ =∫[S] dD‾·dS‾ /dt = dФ/dt

Сис-ма ур-ний Максвелла.

В интегр. форме: 1) 2)

3) 4)

В диффер. форме: 1)rotE‾= –dB‾ /dt 2) rotH‾= j +dD‾ /dt 3) divD =ρ 4)divB =0

Дифф-ое ур-ние электромагн. волны. (no comm)

Классич. т-я электропроводиимости. Природа носителей тока в металлах.

Носителями тока в металлах явл. электроны. Ток в мет-ах при малых разностях потенциалов => элетр. перемещаются по проводнику относительно свободно. У метал. валентные электроны слабо связаны с атомами, поэтому, когда атомы формируют кристал. решетку, вал. электр. обобществляются.

Класич. т-я электропров. Друде.

Друде предполож. что электроны в мет. ведут себя также как мол-лы идеального газа, он перенес рез-ты молек.-кин. т-ии на электронный газ. Ск-ть теплов. движ. электронов 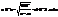при 300К.

При наложении эл. поля, электроны приобретают упоряд. движ <U> =j /n·e (≈10^-3 м/с для меди).

З-н Ома в т-ии Друде.

dI = dU /R => jdS=(dS /ρdl) · Edl => j =E /ρ =σE ((σ [См] -Сименс))