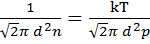Выведите формулу Пуазейля для стационарного движения вязкой жидкости в цилиндрической трубе.

На боковую поверхность выделенного объема жидкости действует сила трения, равная 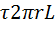. По условию, эти силы равны по величине: ( )

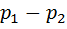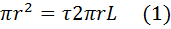
Отсюда получаем: 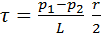(2). Из этого равенства видно, что при течении по трубе касательное напряжение изменяется по сечению трубы по линейному закону от нуля на оси трубы при r = 0 до максимального значения на стенке трубы при r = R.

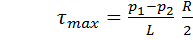(3). Если движение жидкости в трубе ламинарное, то, по закону Ньютона, касательное напряжение трения 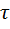определяется формулой 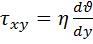. Применительно к данному случаю можно записать эту формулу в виде: 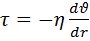. (4)

Знак “минус” берется потому, что 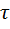- величина положительная, а при выбранной нами системе координат d 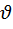/dr - отрицательная. Подставляя (4) в (2), получим: 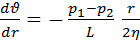. Интегрируя это уравнение, получим: 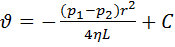(5).

Постоянную интегрирования C найдем из условия прилипания вязкой жидкости к стенкам трубы, т.е. 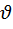= 0 при r = R (R - радиус трубы), отсюда: C= 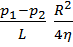(6). Подставляя (6) в (5), получаем: 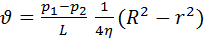(7). Из этого выражения видно, что скорость распределена по сечению трубы по параболическому закону. Величина ее равна нулю на стенке трубы при r = R и достигает максимального значения при r = 0. 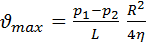(8). Зная распределение скорости по сечению трубы, можно подсчитать секундный объемный расход жидкости q через поперечное сечение трубы. Для этого выделим в сечении трубы элементарное кольцо радиусом r и толщиной dr, настолько малой, чтобы внутри этого кольца скорость течения жидкости можно было считать постоянной.

Тогда через поперечное сечение тонкого кольца площадью 2prdr за секунду пройдет объем жидкости: dq= 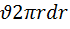(9). Подставляя сюда значение скорости из формулы

(7) и интегрируя по всему сечению трубы, найдем секундный объемный расход жидкости: q=2 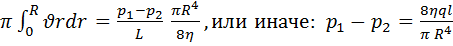(10).

Равенство (10) выражает так называемый закон Пуазейля: paзность давлений, необходимая для того, чтобы через сечение трубы проходил в единицу времени заданный объем жидкости q, при ламинарном течении пропорциональна длине трубы, вязкости жидкости и обратно пропорциональна четвертой степени радиуса трубы. Закон Пуазейля используется для экспериментального определение вязкости h по измеренным значениям секундного объемного расхода жидкости q, радиуса трубы R и

перепада давления 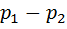на участке трубы длиной L по формуле:

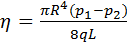
40. Что называется длиной свободного пробега молекул? Как найти эту величину?

Расстояние, которое молекула проходит между двумя последовательными соударениями, называется длиной свободного пробега молекулы. Эта величина для различных молекул может сильно различаться. Даже для одной и той же молекулы от соударения к соударению она может меняться с очень широким интервалом. Однако

среднее значение этой величины для данного состояния газа является величиной постоянной. Средняя длина свободного пробега молекул зависит от числа молекул в единице объема газа. Кроме того, чем больше размер молекулы, тем меньше средняя длина свободного пробега.

Основные количественные данные для определения длины свободного пробега молекул в газе и их эффективных диаметров можно получить из исследований, так называемых явлений переноса, к которым относятся диффузия, теплопроводность, внутреннее трение (вязкость). В частности, из молекулярно-кинетической теории следует, что коэффициент вязкости (или просто вязкость) газа связан со средней длиной свободного пробега молекул соотношением:

η = ρλ <U >, где ρ – плотность воздуха, η – его вязкость, λ – средняя длина свободного пробега молекул, <U > – средняя скорость молекул.

Определив из опыта вязкость и зная среднюю скорость молекул, можно определить среднюю длину свободного пробега. Вязкость воздуха можно определить по формуле Пуазейля: η = 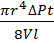, где r – радиус капилляра; l – длина капилляра; t – время, за которое протекает объем воздуха V через капилляр.

<l>= 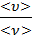где 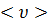средняя скорость ,а 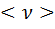частота столкновении. <l>=