Составители Г. Г. Кривнева, В. В. Шаталова

Кафедра химия

Контрольные задания

По физической химии

Методические указания для студентов 2-го курса

заочного обучения специальности

«Производство строительных изделий и конструкций»

Воронеж 2004

Составители Г. Г. Кривнева, В. В. Шаталова

УДК 541. 1

Контрольные задания по физической химии. Методические указания для студентов 2-го курса заочного обучения специальности «Производство строительных изделий и конструкций» / Воронеж. гос. арх. – строит. ун – т.; Сост. : Г. Г. Кривнева, В. В. Шаталова. – Воронеж, 2004. - с.

Методические указания предназначены для самостоятельной работы студентов при изучении курса физической химии. Указания включают важнейшие темы дисциплины, краткое изложение теории, приеры решения задач, задачи для самостоятельного решения.

Содержание дисциплины соответствует государственному обраовательному стандарту для специальности 290601 «Производство строительных изделий и конструкций» утвержденному 17. 03. 2000 г.

Табл. Ил. . Библиограф.: назв.

Печатается по рекомендации редакционно – издательского совета Воронежского архитектурно – строительного университета.

Рецензент –

Оглавление

Введение

Раздел I. Основы химической термодинамики……………………..

1.1. Первый закон термодинамики……………………………………..

1.2. Термохимия…………………………………………………………

1.3. Второй закон термодинамики……………………………………..

Раздел 2. Растворы.

2.1. Давление пара разбавленных растворов. Закон Рауля…………..

2.2. Замерзание и кипение растворов………………………………….

Раздел 3. Химическая кинетика. Закон действия масс. Кинетическая классификация химических реакций.

Раздел 4. Фазовые равновесия в гетерогенных системах

Библиографический список рекомендуемой литературы

Основные вопросы для подготовки к экзамену

Варианты контрольных заданий

Введение

Изучение физической химии дает возможность понять законы химии и физики, а также предсказать химические явления и управлять ими. Поэтому знание физической химии для будущих инженеров – технологов открывает большие возможности для решения многообразных задач, встречающихся в практической деятельности.

Методические указания содержат 4 раздела, относящиеся к следующим темам курса физической химии: основы химической термодинамики, растворы, химическая кинетика, фазовые равновесия в гетерогенных двойных системах. Каждый раздел содержит краткое изложение некоторых теоретических вопросов и формулы, необходимые для решения задач; включает решение типовых задач, рассмотрение которых поможет разобраться в аналогичных примерах. Материал необходимо изучать последовательно, используя предложенную литературу. Особое внимание следует обратить на усвоение понятий, определений, законов, вывод уравнений и решение задач.

Студенты выполняют одну контрольную работу. При оформление работы указывается номер шифра, разборчиво – фамилия, имя и отчество исполнителя. Условие задач переписываются полностью, при решение необходимо все расчеты давать с пояснением. Для замечаний рецензента следует оставлять поля. Контрольная работа должна быть выполнена и зачтена до начала экзаменационной сессии. Номер контрольной работы студенты получают у преподавателя кафедры химии.

По своему содержанию указание соответствует рабочей программе по химии, разработанной в соответствии с типовой программой.

Раздел 1. основы химической термодинамики

Первый закон термодинамики

Термодинамический метод является одним из основных методов физической химии, которой дает точные соотношения между энергией и свойствами системы. Термодинамика применяется к системам, находящимся в равновесии, и рассматривает только начальные и конечные состояния.

Первый закон термодинамики – принцип сохранения и превращения энергии в применении к процессам, сопровождающимся выделением или поглощением теплоты – q, а также совершением или затратой работы – А и изменением внутренней энергии системы – Δ U:

d U = δq - δА (1)

Для конечного изменения состояния системы уравнение (1) можно записать:

Δ U = q - А = q - p ΔV, (2)

где p ΔV – работа расширения.

В уравнение (2) величина q считается положительной, если теплота поглощается системой, и отрицательной, если теплота выделяется в ходе процесса; работа А является положительной, если система её совершает; ΔU считается положительной, если внутренняя энергия системы возрастает, и отрицательной, если убывает.

Внутренняя энергия системы складывается из кинетической энергии молекулярного движения, из энергии взаимного притяжения и отталкивания частиц, составляющих систему, из химической внутримолекулярной энергии. Зависит U от природы вещества, его количества, агрегатного состояния, температуры, давления, объема.

Если система подчиняется законам идеального газа, то при постоянной температуреdU = 0; при изменении температуры

dU = ν C_v ∙ dT. Величина работы расширения, совершаемой системой, зависит от условий, в которых происходит изменение объема:

а) при изобарном расширении (Р – const)

А_р = Р (V₂ – V₁)или

А_р = ν R (T₂ – T₁); (3)

б) при изохорном процессе (V – const)

А _v = 0; (4)

в) при изотермическом процессе (Т - const)

А_т = ν R T ln (V₂ / V₁) = ν R T ln (P₁ / P₂) (5)

г) при адиабатном процессе, протекающем без теплообмена системы с внешнем средой (q = const)

А_q = - Δ U, А_q = С_v (T₂ – T₁); (6)

Применительно к различным термодинамическим процессам, идущим в гомогенных системах, уравнение (2) первого закона термодинамики записывается так:

для изобарного процесса (Р – const)

q_p = Δ U + p Δ V; (7)

для изохорного процесса (Δ V = 0)

q_v = Δ U = С_v (T₂ – T₁); (8)

для изотермического процесса (Δ U =0)

q_т = А_т = ν R T ln (V₂ / V₁) = ν R T ln (P₁ / P₂) (9)

Решение типовых задач

Задача 1.Определите количество теплоты, поглощенное системой и величину работы, совершенной при изотермическом (Т=308 К) расширении от давления 5, 0665∙10⁵Па до давления 1, 01325∙10⁵ Па смеси, состоящей из

1,5 моль кислорода и 2 моль азота.

Решение.

Согласно уравнению (2)∆U = q ­ A, при T-constдля гомогенной системы∆U = 0, тогдаq_Т = А_Т.

Работа изотермического процесса рассчитываем по уравнению (5)

А_{Т =} 3,5 ∙ 8,31∙ 308 ln (5,0665∙10⁵/1,01325∙10⁵) = 14413,7 Дж

или 14,413 кДж

Задача 2.Определите изменение внутренней энергии при охлаждении 10 кг воздуха от 300 ⁰ до 0 ⁰С . Удельная теплоемкость воздуха при постоянном объеме выражается уравнением

C_V = 0,7084 + 1,87 ∙10^-4 Т кДж/кг∙К.

Решение.

В изохорном процессе работа расширения не совершается (∆V=0), поэтому из уравнения (2) ∆U_V = q_V.

Изменение внутренней энергии в данном процессе рассчитываем согласно уравнению (8)

T₂

∆U_V = - m C_v (T₂ – T₁) = - m ∫ C_v d T=

T₁

∆U_V = -10 ∫ (0,7084 +1,87 ∙10^-4 Т) dT= -10∙[0,7084(573 –

273)+(1,87 / 2) ∙10^-4(573² – 273²)] = - 2362,5 кДж.

Задачи для самостоятельного решения

1.Для испарения 20 кг спирта при температуре 351 К и давление 1, 01325 ∙10⁵ Па потребовалось 17,01 ∙10⁶ Дж теплоты. При этом образовался пар, занимающий объем 12,2 м³. Определите изменение внутренней энергии, считая пары спирта идеальным газом. Объемом жидкости пренебречь.

Ответ: 15, 774 ∙10⁶ Дж.

2.Определите изменение внутренней энергии при испарение 90 г воды при температуре её кипения. Теплота образования воды 40714,2 Дж/моль, удельный объем водяного пара 1,699 ∙10 ^{– 6}м³/г. Давление 1, 01325 ∙10⁵ Па, объемом жидкости пренебречь.

Ответ: 203, 56 кДж.

3.Теплоемкость кислорода при постоянном объеме выражается уравнением С_v = 0,6527 + 2,5 ∙10 ^{– 4} Т кДж /кг ∙К . Вычислите изменение внутренней энергии при охлаждение 1 кг кислорода от 200⁰ до 0⁰ С.

Ответ: - 149,19 кДж.

4.Газ, расширяясь при постоянном давлении 1, 01325 ∙10⁵ Па от 25 ∙10 ^–3 м³ до 75 ∙10 ^–3 м³ , поглощает 12570 Дж теплоты. Определите изменение внутренней энергии.

Ответ: 7,504 кДж.

5.При адиабатном расширении 5 кг водорода затрачена работа, равная (- 580 кДж). Начальная температура 0⁰ С, теплоемкость водорода при постоянном объеме 1, 04 кДж / кг ∙ К. Определите изменение внутренней энергии системы и конечную температуру процесса.

Ответ: 580 кДж, 384, 5 К.

6.При 17⁰С 10кг воздуха изотермически расширяется от 1,025∙10⁶ Па до 1,340 ∙10⁵ Па. Определите объем воздуха в начале и конце процесса расширения, совершенную при этом работу и количество подведенной теплоты. Средняя молярная масса воздуха 29 г.

Ответ: 1688,5 кДж; 0,811м³; 6, 192 м³

7.Водяной пар в количестве 450г конденсируется при 100⁰С при постоянном давлении. Теплота испарения воды равна 2253, 02 Дж/г. Вычислите работу процесса, количество выделенной теплоты и изменение внутренней энергии системы.

Ответ: - 77, 49 кДж; - 1013, 83 кДж; - 936, 37 кДж.

8.При 0⁰С 5кг азота изотермически расширяется от давления 1,040 ∙ 10⁶ Па до 1,542 ∙10⁵ Па. Определите объем в начале и конце процесса, количество совершенной работы.

Ответ: 0, 4138 м³; 2,63 м³; 769, 4 кДж.

9.Рассчитате изменение внутренней энергии при нагревании 2кг ά – кварца от 298 до 800 К, если зависимость теплоемкости ά – кварца от температуры выражается уравнением

С_v = 0,83 +34,3∙10^–3 Т кДж / кг ∙ К. Объем системы не меняется.

Ответ: 19623, 98 кДж.

10.Работа, затраченная на адиабатное сжатие 3кг воздуха, равна (-471 кДж). Начальная температура 15⁰С. Определите изменение внутренней энергии системы и конечную температуру процесса. Средняя теплоемкость воздуха при сжатии равна 0, 732 кДж/кг∙К.

Ответ: 471 кДж; 502,5 К.

11.Рассчитайте изменение внутренней энергии при испарение 5 моль спирта при температуре 79⁰С, если мольная теплота парообразования спирта равна 39, 509 кДж/моль. Объемом жидкости пренебречь.

Ответ: 182,2кДж.

12.10л азота, взятого при температуре 273 К и давлении 5,0662 ∙10⁵ Па, расширяется изотермически до давления 1, 01325 ∙10⁵ Па. Рассчитайте работу, совершенную системой и поглощенную в ходе процесса теплоту.

Ответ: 1626, 3 кДж.

13.Вычислите изменение внутренней энергии при испарении 50г толуола при 30⁰С и давлении 1,01325 ∙10⁵ Па, приняв, что пары толуола подчиняются законам идеального газа и объем жидкости незначителен по сравнению с объемом пара. Теплота испарения толуола 347, 8 Дж/г; молярная масса толуола – 92 г/моль.

Ответ: 16, 021 кДж.

14.Вычислить изменение внутренней энергии при нагревании 5кг азота от 0⁰ до 500⁰С, если удеальная теплоемкость азота при постоянном объеме выражается уравнением

С_v= 0,7084 +1,8 ∙10 ^–3 Т кДж / кг ∙ К.

Ответ: 2006, 3 кДж.

15.Определите изменение внутренней энергии при испарении 20г спирта при температуре кипения и давлении 1,01325 ∙10⁵ Па, если известно, что удельная теплота испарения спирта равна 856,9 Дж/г, а удельный объем пара при температуре кипения равен 607 ∙10 ^–6 м³/г. Объемом жидкости пренебречь.

Ответ: 159, 24 Дж.

16. Какое количество теплоты затрачено и какая работа будет совершена, если 51г аммиака, занимавшего при 27⁰С объем 25∙10 ^–3 м³, расширяется при постоянной температуре до 75∙10 ^–3 м³?

Ответ: 8226,9 Дж.

17.10г кислорода сжимается адиабатически, при этом температура повышается от 298 К до 502 К. Определите работу, затраченную на адиабатическое сжатие кислорода, изменение внутренней энергии системы. Средняя мольная теплоемкость кислорода при постоянном давлении равна 20,77Дж/моль∙К.

Ответ: 1323.9 Дж.

18.Какое количество теплоты выделяется при изотермическом сжатии идеального газа от 30∙10 ^–3 м³ до 15∙10 ^–3 м³, если он был взят при 0⁰С и давлении 1,850 ∙10⁵ Па.

Ответ: 3811,5 Дж.

19.Определите изменение внутренней энергии при испарении 2 моль толуола при 50⁰С и давлении 1,01325∙10⁵ Па, приняв, что пары толуола подчиняются законам идеальных газов и объем жидкости незначителен по сравнению с объемом пара. Теплота испарения толуола 31997,6 Дж/моль.

Ответ: 58,62 кДж.

20.Какое количество теплоты выделяется при изотермическом сжатие идеального газа от 24∙10 ^–3 м³ до 3∙10 ^–3 м³, если он был взят при 17⁰С и давлении 1,454∙10⁵ Па?

Ответ: - 7266,3 Дж.

Термохимия

Раздел химической термодинамики, в котором изучаются тепловые эффекты химических процессов, называется термохимией.

Тепловой эффект процесса, протекающего при постоянном давлении или объеме, не зависит от пути следования процесса, а зависит только от природы исходных и конечных веществ и их состояния (закон Гесса).

В термохимических расчетах используют следующие два следствия закона Гесса:

а) тепловой эффект процесса равен разности между суммой теплот образования продуктов (∆H^обр_прод..) и суммой теплот образования исходных веществ (∆H^обр_исх..) с учетом стехиометрических коэффициентов в уравнении реакции;

б) тепловой эффект процесса равен разности между суммой теплот сгорания исходных веществ (∆H^сгор_исх..) и суммой теплот сгорания продуктов реакции (∆H^сгор_прод..) с учетом стехиометрических коэффициентов в уравнении реакции.

Закон Гесса и следствия позволяют вычислять тепловые эффекты различных процессов на основе табличных данных о теплотах образования неорганических веществ и теплотах сгорания органических соединений при стандартных условиях (Р= 101325 Па, Т= 298 К). Поскольку расчеты в химии и химической технологи чаще всего приходится производить для изобарных процессов, то для данных процессов тепловой эффект обозначают через энтальпию-∆H:

∆H = ∆U + p∆V; (10)

q_V = ∆U , q_Р = ∆H , q_Р = q_V +p∆V. (11)

Для определения тепловых эффектов при температурах, отличных от стандартной, необходимо учесть температурные зависимости теплоемкостей веществ, которые выражаются степенными рядами:

С_Р = а + вТ + сТ² + …

С_Р = а + вТ + с^΄ Т^-2 + … (12)

Уравнение Кирхгофа, выражающее зависимость теплового эффекта от температуры, будет иметь вид:

Т₂

∆H_Т = ∆H₂₉₈ + 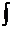∆С_Р∙ dТ ,

Т₁

Т₂

∆H_Т = ∆H₂₉₈ + 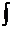(∆а + ∆dT + ∆cT² + ∆c΄T^-2)dT (13)

Т₁

где ∆а, ∆b, ∆с, ∆c΄— алгебраические суммы постоянных а, b, с, c΄.

Решение типовых задач

Задача 1.Определите тепловой эффект реакции

Al₂O₃ + 3SO₃ → Al₂(SO₄)₃

при 298 К и 101325 Па.

Решение. Для определения ∆H_реакц. воспользуемся следствием из закона Гесса.

∆H_реакц.. = ∆H^обр Al₂(SO₄)₃ - (∆H^обр Al₂O₃+ 3∆H^обр SO₃).

Тепловые эффекты образования веществ представлены в таблице 1

∆H^обр Al₂O₃= -1675 кДж/моль; ∆H^обр SO₃= -395,2 кДж/моль;

∆H^обр Al₂(SO₄)₃= -3434 кДж/моль.

∆H_реакц.= -3434 +1675+3∙395,2= -573,4 кДж.

Задача 2. Рассчитайте тепловой эффект процесса при 600 ⁰С, протекающего по уравнению СО +Н₂О_(пар) → СО₂ +Н₂, используя температурные зависимости теплоемкостей реагирующих веществ (Дж/моль∙К):

С_Р(СО) = 28,41 + 4,1∙10^-3Т – 0,46∙10⁵Т^-2;

С_Р(Н₂О) =30,00 + 10,7∙10^-3Т + 0,33∙10⁵Т^-2;

С_Р(СО₂) = 44,14 + 9,0∙10^-3Т + 8,53∙10⁵Т^-2;

С_Р(Н₂) = 27,28 + 3,2∙10^-3Т + 0,50∙10⁵Т^-2.

Решение.По теплотам образования веществ, взятым из таблицы 1, подсчитаем тепловой эффект процесса при стандартных условиях (Т-298К);

∆H₂₉₈ = ∆H^обр СО₂ -∆H^обр СО - ∆H^обр Н₂О =

= -393,51+110,5+241,84=-41,170 кДж.

Определяем ∆а, ∆b, ∆c΄:

∆а= 27,28+44,14-30,00-28,41=13,01,

∆b= (3,2+9,0-10,7-4,1)∙10^-3 = -2,6∙10^-3,

∆c΄= (0,5-8,53+0,46-0,33) ∙10⁵ = -7,9∙10⁵.

Т= 60+273=873 К.

Тепловой эффект процесса при 600 ⁰С находим по уравнению (13)

∆H₈₇₃ = ∆H₂₉₈ + 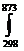(13,01 - 2,6∙10^-3Т - 7,9∙10⁵Т^-5)dT =

= -41170+13,01(873-298)-1/2∙2,6∙10^-3∙(873²-298²)+

+ 7,9∙10⁵(1/873- 1/298)=-36307 Дж или ∆H₈₇₃=-36,307 кДж.

Задачи для самостоятельного решения

21.Определите теплоту сгорания этилена

С₂Н₄ + 3О₂ → 2СО₂ + 2Н₂О_(ж),

исходя из следующих данных: ∆H^обр С₂Н₄= 62,01 кДж/моль;

∆H^обрН₂О= -284,9 кДж/моль;∆H^обр СО₂= -393,9 кДж/моль.

Ответ: -1419,6 кДж/моль.

22.Найдите разность междуq _p и q _vпри 25⁰С для следующих реакций:

N₂ + 3 H₂ → 2NH₃; 2 C + O₂ → 2 CO.

Ответ: -4955,1 Дж; - 2477,5 Дж.

23.Теплота диссоциацииСаСО₃ → СаО + СО₂ при 900⁰С составляет 178, 3 кДж/моль. Теплоемкости веществ Дж/моль∙К:

С_р (СаСО₃) = 104,5 + 21,9∙10^-3Т – 25,9∙10⁵ Т^-2;

С_р (СаО) = 49,6 + 4,5∙10^-3Т – 6,9∙10⁵ Т^-2;

С_р (СО₂) = 44,1 + 9,0∙10^-3Т – 8,5∙10⁵ Т^-2.

Вычислите теплоту диссоциации при 1000⁰С.

Ответ: 176, 3 кДж.

24.Определите количество теплоты, выделяющейся при гашении 500 кг извести водой:

СаО + Н₂О → Са (ОН)₂при 25⁰С

Для решения задачи теплоты образования веществ (∆Н₂₉₈) возьмите из таблицы 1.

Ответ: 589, 3 кДж.

25.Тепловой эффект реакции 2 Fe + 3/2 O₂ → Fe₂O₃ при 18⁰С и постоянном давлении равен – 823, 3 кДж/моль. Определите q _v для этой реакции при той же температуре.

Ответ: - 817, 67 кДж.

26.Рассчитать тепловой эффект при 1000 К процесса

СН₄ → С + 2Н₂, если ∆Н₂₉₈= 74, 9 кДж/моль. Теплоемкости веществ Дж/моль∙К:

С_р (С) = 11,2 + 10,9 ∙10^-3Т;

С_р (Н₂) = 27,2 + 3,8 ∙10^-3Т;

С_р (СН₄) = 22,4 +43,2∙10^-3Т.

Ответ: 99,4 кДж/моль.

27.Определите теплоту образования сероуглерода по уравнению СS₂ + 3О₂ → СО₂ + 2 SО₂, если известно, что тепловой эффект реакции равен (–1109.9) кДж.

∆Н^обр.SO₂ = -297,1 кДж/моль; ∆Н^обр.СO₂=- 393,7 кДж/моль.

Ответ: 122,0 кДж/моль.

28.Вычислите теплоту образования бензола

6 С + 3 Н₂ → С₆ Н₆, если теплоты сгорания водорода, углерода и бензола соответственно равны: -285,0; - 394,0; -3282,4 (кДж/моль).

Ответ: - 63,4 кДж/моль.

29.Теплота образования паров воды по уравнению

Н₂ + ½ О₂ → Н₂О _(пар) при 25⁰С равна (– 242,0) кДж/моль. Вычислите тепловой эффект этой реакции при 1000 К пользуясь уравнениями теплоемкостей реагирующих веществ (Дж/моль∙К):

С_р (Н₂О) = 30,2 +11,3 ∙10^-3Т;

С_р (Н₂) = 29,1 – 0,84 ∙10^-3Т;

С_р (О₂) = 31,5 + 3,4 ∙10^-3Т.

Ответ: - 247,5 кДж.

30. Тепловой эффект реакции Мq(OH)₂ → МqО + Н₂О _(пар), протекающей в открытом сосуде при 400 К и 101325 Па, составляет 89, 03 кДж. Как будет отличаться от этого значения тепловой эффект, если реакцию проводить при той же температуре, но в закрытом сосуде?

Ответ: 85, 7 кДж.

31. Рассчитате расход теплоты на получение 100м³ водорода в ходе процесса

СН₄ + СО₂ → 2 СО + 2 Н₂

Данные по теплотам образования веществ возьмите из таблицы 1.

Ответ: 5, 552∙ 10⁵ кДж.

32. Сколько выделится теплоты при гашении 112 кг извести по реакции СаО + Н₂О_(ж) → Са(ОН)₂? Теплоты образования веществ возьмите из таблицы 1.

Ответ: 136 ∙ 10³ кДж.

33.Вычислите тепловой эффект реакции Ν₂ + 3 Н₂ → 2 ΝН₃ при 500⁰ С, если уравнения для теплоемкостей (Дж/моль∙ К) реагирующих веществ имеют вид:

С_р (ΝН₃) = 29, 6 + 25, 5 ∙ 10 ^–3 Т;

С_р (Н₂) = 29, 1 – 0, 84 ∙ 10 ^–3 Т;

С_р (Ν₂) =27, 8 + 4, 3 ∙ 10 ^–3 Ти теплота реакции при 25⁰ С

равна (– 92, 4) кДж

Ответ: - 107, 2 кДж

34.Определите количество поглощенной теплоты при растворении 1 м³ оксида углерода СО + Н₂О_(ж) → СО₂ + Н₂. Данные по теплотам образования веществ при стандартных условиях возьмите из таблицы 1.

Ответ: 125, 1 кДж.

35. Рассчитайте теплоту образования нафталина при 25⁰ С, если тепловой эффект реакции

С₁₀Н₈ + 12 О₂ → 10 СО₂ + 4 Н₂О_(ж) равен (– 5162) кДж

ΔН^обр СО₂= - 393, 8 кДж/моль, ΔН^обрН₂О_(Ж) = - 286, 0 кДж/моль

Ответ: 84 кДж/моль.

36.Определить тепловой эффект реакции

Са(ОН)₂ → СаО + Н₂О_(г) , если она протекает в автоклаве при постоянном объеме и 298 К. Тепловые эффекты образования веществ при стандартных условиях возьмите из таблицы 1.

Ответ: 106, 82 к Дж.

37.При стандартных условиях тепловой эффект процесса

С₂Н₅ОН_(г) → C₂H₄ + H₂О_(г)равен 45, 8 кДж. Вычислите тепловой эффект этой реакции при 400 К, если температурная зависимость теплоемкостей (Дж/моль·К) веществ выражается уравнениями:

С_р (H₂О_(г)) = 30, 1+11, 3∙ 10^-3 Т,

С_р (C₂H₄) = 4, 2+154, 7∙ 10^-3 Т,

С_р (С₂Н₅ОН_(г)) = 20, 7+205, 5∙ 10^-3 Т.

Ответ: 45, 78 кДж.

38.Какое количество тепла надо затратить, чтобы прошел процесс разложения 0, 2 м³ СО₂ по реакции 2СО₂ → 2СО + О₂при стандартных условиях. Данные возьмите из таблицы 1.

Ответ: 2517, 3 кДж.

39.Рассчитайте теплоту образования аммиака при стандартных условиях, если тепловой эффект реакции

NH₄Cl_(тв) → NH₃ + HCl_(г)равен 175, 2 кДж, а

∆Н^обр NH₄Cl= - 313,8 кДж/моль,∆Н^обр HCl = -92, 38 кДж/моль.

Ответ: -46, 22 кДж.

40.Тепловой эффект сгорания графита при 298 К равен

–393,8 кДж/моль. Молярные теплоемкости для этих веществ соответственно равны 8,65 кДж/моль∙К и 6, 06 кДж/моль∙К. Рассчитайте тепловой эффект перехода графита в алмаз при 273 К.

Ответ: -1835, 2 Дж.

Второй закон термодинамики

Второй закон термодинамики устанавливает: возможен или невозможен при данных условиях тот или иной процесс, до какого предела он может протекать и какая полезная работа совершится при этом. Применительно к химическим процессам второй закон можно сформулировать так: всякое химическое взаимодействие при неизменных давлении или объеме и постоянстве температуры протекает в направлении уменьшения изобарно-изотермического ∆Gили изохорно-изотермического∆F потенциалов. Изменение G и F можно рассчитать по уравнениям

∆G = ∆H - T∆S; ΔF = ∆U - T∆S, (14)

где ∆S – изменение энтропии в ходе процесса, физический смысл энтропии – энергетическая мера беспорядка в системе.

Если процессы совершаются в системах, свойства которых близки к идеальным, то изменение энтропии определяется по уравнениям

∆S= ν Rln(V₂/V₁) + ν C_Vln(T₂/T₁), (15)

∆S = ν Rln(Р₁/Р₂) + ν C_рln(T₂/T₁) (16)

Для реальных систем

Т₂

∆S = ν ∫ ∆ C_р (dТ/Т) (17)

Т₁

При переходе вещества из одного агрегатного состояния в другое изменение энтропии рассчитывается

∆S = ∆H_пер / Т = L / Т,(18)

L – скрытая теплота фазового превращения (испарения, плавления и др.),

Т – температура фазового перехода.

Размерность энтропии Дж / моль∙К

Пределом протекания химической реакции ( т. е. условиям наступления равновесия, для которого ∆G = 0или ∆ F = 0) является достижением некоторого минимального значения G иF.

Если расчет показал, что в ходе процессов изобарно – изотермический или изохорно – изотермический потенциалы уменьшаются (∆G < 0 или ∆ F < 0), то данные процессы при заданных условиях возможны и идут самопроизвольно. При ∆G > 0или

∆ F > 0 процессы не могут при заданных условиях (V, Т или Р, Т) протекать самопроизвольно и возможны лишь при получении работы извне.

Решение типовых задач

Задача 1.Определите изменение энтропии при нагревании

30 г ледяной уксусной кислоты от температуры плавления 16, 6 до 60⁰ С. Теплота плавления 194 Дж/г, массовая теплоемкость уксусной кислоты выражается уравнением С_р =1,9 + 3, 9∙10 ^–3 ТДж/г∙К.

Решение. Общее изменение энтропии ∆Sравно сумме изменений энтропии при плавлении ∆S₁и при нагревании ∆S₂ жидкой уксусной кислоты от температуры плавления до заданной температуры 60⁰ С.

По формуле (18) рассчитаем изменение энтропии при плавлении:

∆S₁ =( m ∙ L) / Т_пл. = 30 ∙ (194 / 289, 6) = 20, 09 Дж/К

Для вычисления ∆S₂ используем формулу (17)

333

∆S₂ = m ∙∫(1, 96 + 3, 9 ∙ 10^-3 Т) ∙ (d Т/Т) =

289, 6

30 [1, 96 ∙ 2, 303 lg(333 / 289, 6) + 3, 9 ∙ 10^-3(333 – 289, 6) ];

∆S₂ = 13, 26 Дж/К;

∆S= 20, 09 +13, 26 = 33, 35 Дж/К.

Задача 2.Определите изменение изобарно-изотермического потенциала при стандартных условиях для реакции

Fe₃O₄ + СО → 3 FeО + СО₂ и решите вопрос о возможности самопроизвольного протекания её при указанных условиях.

Рассчитайте температуру, при которой наступит состояние равновесия данной системы.

Решение.Изменение изобарно-изотермического потенциала при стандартной температуре 298 К определяем по формуле (14)

∆G_реакц. = ∆Н⁰_реакц. - Т∆ S⁰_реакц.

Значение ∆Н⁰₂₉₈и ∆ S⁰₂₉₈ для веществ, участвующих в реакции:

∆Н^обрFeO= - 266, 9 кДж/моль ∆ S⁰ FeO= 58, 8 Дж/моль∙К

∆Н^обрСО₂ = -383, 8 кДж/моль ∆ S⁰ СО₂ = 213 Дж/моль∙К

∆Н^обрСО= - 110, 6 кДж/моль ∆ S⁰СО = 198, 0 Дж/моль∙К

∆Н^обр Fe₃O₄= -1118, 7 кДж/моль ∆ S⁰ Fe₃O₄ = 151, 5 Дж/моль∙К

∆Н_реакц. = ∆Н^обрСО₂ + 3 ∆Н^обрFeO - ∆Н^обр_СО - ∆Н^обр Fe₃O₄.

∆Н_реакц. = -383, 8 -3 ∙266, 9 + 110, 6 +1118, 7= 34, 8 кДж.

∆ S_реакц. = S⁰ СО₂ + 3 S⁰ FeO - S⁰СО - S⁰ Fe₃O₄ .

∆ S_реакц.=213 + 3∙58, 8 - 198, 0 - 151, 5 = 40, 7 Дж/К

∆G_реакц. = 34800 – 40, 7 ∙ 298 = 22672 Дж = 22, 67 кДж.

Итак, ∆G_реакц > 0. Следовательно, при стандартных условиях самопроизвольный процесс восстановления Fe₃O₄ оксидом углерода невозможен.

Равновесие системы наступает тогда, когда ∆G=0.

0=∆Н_реакц.- Т_рав.· ∆ S_реакц. ;отсюдаТ_равн. = (∆Н_реакц. / ∆ S_реакц.) =

= 34, 8 / 0, 0407 = 855 К или 582⁰ С.

Задачи для самостоятельного решения

41. Рассчитайте изменение изобарно-изотермического потенциала в ходе процесса образования алюмината кальция

СаО + Аl₂O₃ → СаО ∙ Аl₂O₃ при температуре 1400 К и решить вопрос о возможности его протекания при данной температуре. Данные для решения возьмите из таблицы 1.

Ответ: - 41, 7 кДж.

42.Вычислите суммарное изменение энтропии при нагревании 1 моля воды от температуры плавления до полного испарения при температуре кипения. Теплота плавления льда 335, 2 Дж/г, теплота парообразования воды 2260 Дж/г, массовая теплоемкость воды 4, 188 Дж/г∙К.

Ответ: 154, 67 Дж.

43.Определите изменение изобарно-изотермического потенциала в ходе реакции Ν₂ + 2 Н₂О_(ж)→ΝН₄ΝΟ₂и дайте заключение о возможности её протекания при стандартных условиях, если ΔG⁰ Н₂О _(ж) = - 237, 5 кДж/моль ΔG⁰ ΝН₄ ΝΟ₂ = 115, 94 кДж/моль

Ответ: 590, 94 кДж.

44. Рассчитайте изменение энтропии для 1 кг воздуха при нагревании его от – 50 до +50⁰ С, при этом происходит изменение давления от 10⁶ до 10⁵ Па. Массовая теплоемкость воздуха 1, 005 Дж/г∙К. Средняя молярная масса воздуха 29.

Ответ: 1032, 5 Дж.

45. Чему равно изменение энтропии 128 г нафталина при нагревании его от 0 до 80, 4⁰С (температура плавления), если теплота плавления 149, 6 Дж/г, а средняя массовая теплоемкость кристаллического нафталина 1, 315 Дж/ г∙К.

Ответ: 97, 62 Дж/К.

46.Вычислить изменение изобарно-изотермического потенциала в ходе процесса СаСО₃ → СаО + СО₂ и решить вопрос о возможности его протекания при 900⁰С. Рассчитайте температуру, при которой система достигнет состояния равновесия. Данные для решения возьмите из таблицы 1.

Ответ: - 10, 87 кДж.

47.Определите изменение изобарно-изотермического потенциала в ходе процесса образования силиката магния

MgO +SiO₂→ MgO ∙ SiO₂ и решите вопрос о его протекании при стандартных условиях. Данные для решения возьмите из таблицы 1.

Ответ: - 35, 04 кДж.

48. Определите изменение энтропии при стандартных условиях для процессов: 2 Н₂S + SO₂ → 2 Н₂O_(ж) - 3 S ;

Са(ОН)₂ + СО₂ → СаСО₃ + Н₂О_(ж)

и объясните её уменьшение в ходе данных процессов.

Ответ: - 423, 8 Дж/К; -134, 5 Дж/К.

49. Самопроизволен ли процесс гашения извести при стандартных условиях, протекающий по уравнению

СО₂ + Н₂О_(ж)→ Са(ОН)₂.

Ответ мотивируйте, рассчитав изменение ΔG⁰ для данного процесса; данные для решения возьмите в таблице 1.

50.Вычислите изменение энтропии при нагревании 1 моль

α – кварца –SiO₂ от 258 до 900 К, если зависимость теплоемкости α – кварца от температуры выражается уравнением

С_р = 46, 94 +34, 31 ∙ 10^-3 ТДж/ моль ∙ К.

Ответ: 72, 53 Дж/К.

51. Нагревают 14 кг азота от 273 до 373 К при постоянном объеме. Рассчитайте изменение энтропии в этом процессе. Зависимость теплоемкости азота при постоянном объеме от температуры выражается уравнением

С_v = 29, 7 + 4, 27 ∙ 10^-3 ТДж/ моль ∙ К

Ответ: 3444, 2 Дж/К.

52.Определите изменение изобарно-изотермического потенциала для процесса Mq + CO₂ → MqCO₃, при стандартных условиях и рассчитайте температуру, при которой система достигает состояния равновесия. Для решения воспользуйтесь данными из таблицы 1.

Ответ: 66, 4 кДж; 677, 4 К.

53.В одном сосуде емкостью 3 м³ находиться 2 кг водорода, в другом емкостью 6 м³ – 32 кг кислорода при той же температуре. Вычислите изменение энтропии при диффузии в результате соприкосновении содержимого этих сосудов. Считать, что водород и кислород являются идеальными газами.

Ответ: 12, 49 ∙ 10³ Дж/К.

54.Рассчитате изменение энтропии при нагревании 2, 7 кг воды от 293 К до 390 К. Теплота испарения воды 2260, 9·10³ Дж/кг, массовая теплоемкость жидкой воды 4, 2 ∙ 10³ Дж/кг ∙ К, пара –

2, 0 ∙ 10³ Дж/кг ∙ К.

Ответ: 20, 14 ∙ 10³Дж/К.

55. Определите изменение изобарно-изотермического потенциала при температуре 298 К для реакции образования трехкальциевого силиката 3 CaO + SiO₂ → 3 CaO·SiO₂. Возможен ли данный процесс при стандартных условиях? Данные для решения возьмите из таблицы 1.

Ответ: 456, 3 кДж.

56.Массовая теплоемкость железа равна 0, 486 Дж/г·К. Определите изменение энтропии при нагревании 1 кг железа от 100 до 150 ⁰С.

Ответ: 61, 14 Дж/К.

57.Рассчитате изменение изобарно-изотермического потенциала при Т–298 К для процесса MqO + H₂ → H₂O_(Ж) + Mq. Определите, при какой температуре в системе установиться равновесие. Величины ∆Н⁰₂₉₈ и S⁰₂₉₈ для веществ возьмите из таблицы 1.

Ответ: 332 кДж; 5751 К.

58. Определите изменение энтропии при Т=298 к в ходе следующих реакций: С + О₂ → 2 СО; FeO+CO→Fe+CO₂. Для решения воспользуйтесь данными таблицы 1.

Ответ: 176 Дж/К; -13, 2 Дж/К.

59. Возможен ли процесс синтеза аммиака при стандартных условиях 3 Н₂ + N₂→2NH₃? Величины ∆Н⁰₂₉₈ иS⁰₂₉₈ для веществ возьмите из таблицы 1.

60.Вычислите изменение энтропии при охлаждении 12 ∙10^-3кг кислорода от 290 до 233 К и одновременном повышении давления от 1 ∙ 10⁵ до 60, 6 ∙ 10⁵ Па. Если теплоемкость кислорода

С_р(О₂) = 32, 9 Дж/моль ∙ К.

Ответ: -15, 2 Дж/К.

Ра