Экстремум функции нескольких переменныx

переменных может иметь максимум или минимум (экстремум) только в точках, лежащих внутри области определения функции, в которой все ее частные производные первого порядка равны нулю или не существует хотя бы одна из них. Такие точки называются критическими. Названные условия являются необходимыми условиями экстремума, но еще не достаточными (они могут выполняться и в точках, где нет экстремума). Чтобы критическая точка была точкой экстремума, должны выполняться достаточные условия. Сформулируем достаточные условия экcтремума для функции двух переменных. Пусть точка M_o(x_o, y_o) - критическая точка функции z = f(x, y), т.е. 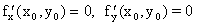, и функция
z = f(x, y) имеет непрерывные вторые частные производные в некоторой окрестности точки M_o(x_o, y_o). Обозначим 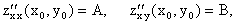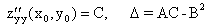. Тогда:

1) если D > 0, то функция z имеет экстремум в точке M_o: максимум при A < 0, минимум при A > 0;

2) если D < 0, то экстремума в точке M_o нет;

3) если D = 0, то требуется дополнительное исследование.

Пример 1. Исследовать функцию z = y⁴ - 2xy² + x² + 2y + y² на экстремум.

Решение. Находим частные производные: 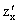= - 2y² + 2x, 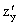= 4y³ - 4xy +2 +2y. Для отыскания критических точек решим систему уравнений: .

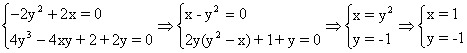Итак, M_o(1,-1) -единственная точка, “подозрительная на экстремум”. Находим вторые частные производные: 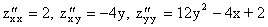, следовательно, A=2, B=4, С=10, D = 4, т.е. D > 0, функция имеет экстремум в точке M_o - минимум (A>0). Вычислим

z _min = (-1)⁴ - 2×1×(-1)² +1 - 2 +1 = -1.

Проведем обобщение.

Определение. Точка М (х₀, у₀) называется точкой максимума (минимума) функции z = f(x, y), если существует окрестность точки М, такая, что дли всеx точек (x, y) из этой окрестности выполняется неравенство

f(x₀, y₀) ≥ f(x, y)

(f(x₀, y₀) ≤ f(x, y)).

Исследование функции двух переменныx на экстремумрекомендуется проводить по следующей схеме:

1. Найти частные производные функции z'_x и z'_y.

2. Решить систему уравнений z'_x = 0, z'_y = 0 и найти критические точки функции.

3. Найти частные производные второго порядка, вычислить иx значения в каждой критической точке и с помощью достаточного условия сделать вывод о наличии экстремумов.

Необходимое и достаточное условие экстремум функции нескольких переменных

Необходимые условия экстремума дифференцируемой функции нескольких переменных выражается следующими теоремами:

Теорема 1.

В точке экстремума дифференцируемой функции все ее первые частные производные равны нулю,если 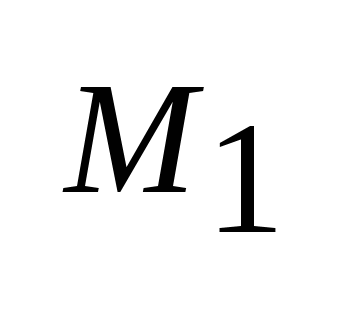-экстремум ф-ции.

Теорема 2.

Пусть функция z=/(х,у) имеет непрерывные частные производные до второго порядка включительно в некоторой окрестности точки М₀(а,b).

Если ее первые частные производные в точке М₀ равны нулю, а вторые принимают значения

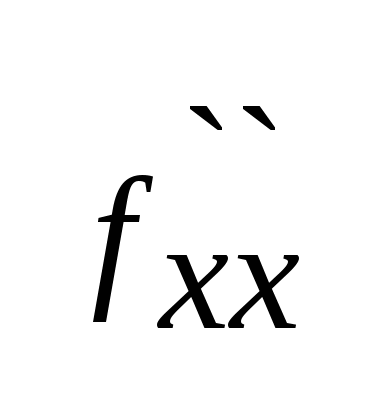(a,b)=A, 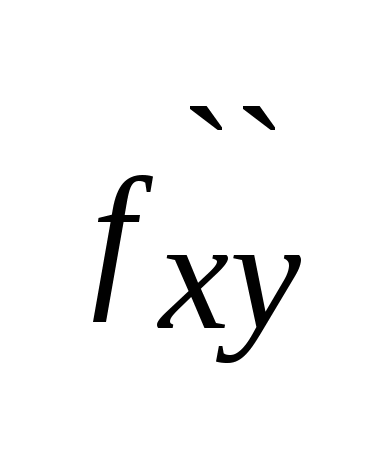(a,b)=B, 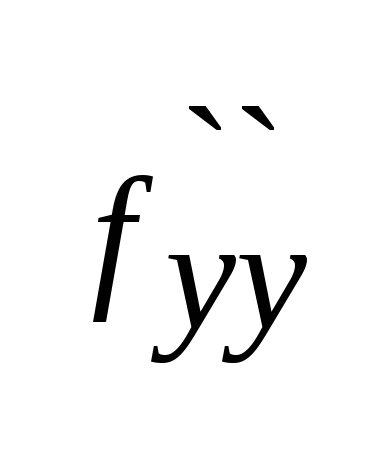(a,b)=C,

Топри

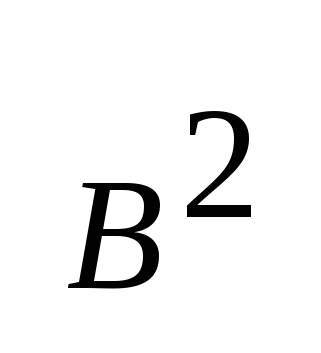-АС<0 и А>0

точка М₀является точкой минимума данной функции, а при

В²-АС<0, А<0

точкой максимума, при

В²-АС>0

в точке М₀экстремума нет.

Теорема (достаточное условие экстремума функции двух переменныx). Пусть функция z = f(x, y):

а) определена в некоторой окрестности критической точки (x₀, y₀), в которой f'_x(x₀, y₀) = 0 и f'_y(x₀, y₀) = 0;

б)имеет в этой точке непрерывные частные производные второго порядка f''_xx(x₀, y₀) = A; f'_xy(x₀, y₀) = f''_yx(x₀, y₀) = B; f'_yy(x₀, y₀) = C. Тогда, если Δ = AC - B² > 0, то в точке (x₀, y₀) функция z = f(x, y) имеет экстремум, причём если A < 0 - максимум, если A > 0 -минимум. В случае Δ = AC - B² < 0, функция z = f(x, y) экстремума не имеет. Если Δ = AC - B² = 0, то вопрос о наличии экстремума остаётся открытым.