Расчет шпунтового ограждения, погружаемого в связный грунт при наличии

Слоя несвязного грунта.

Необходимо определить глубину погружения шпунта ниже дна котлована и марку применяемого шпунта. Сооружение шпунтового ограждения производится в русле реки. В основании фундамента находится два слоя грунта. Котлован под ростверк заглублен в связный грунт.

Характеристики грунта:

1 слой ¾ несвязный грунт

· песок мелкий;

· толщина пласта ¾ м;

· удельный вес ¾ тс/м³;

· коэффициент пористости ¾ ;

· угол внутреннего трения ¾ .

2 слой ¾ связный грунт

· суглинок консистенции ;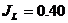

· коэффициент пористости ¾ ;

· удельный вес ¾ тс/м³;

· удельное сцепление ¾ кгс/см² (2.8 тс/м²);

· угол внутреннего трения ¾ .

Характеристики котлована:

· глубина воды ¾ м;

· удельный вес воды ¾ 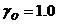тс/м³;

· глубина котлована ¾ м.

СХЕМА 1: принимаем к расчету шпунтовую стенку без распорного крепления. Учитываем сцепление шпунта с грунтом (рис. 5.2, А).

При устройстве ограждения без тампонажного подушки (для связных грунтов она ненужна) минимальную глубину забивки шпунта ниже дна котлована определяют по формуле

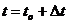
Глубину 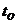определяем из условия обеспечения устойчивости стенки против опрокидывания, считая ось поворота стенки расположенной на этой глубине.

Удельный вес несвязного грунта во взвешенном состоянии составляет

тс/м³

Интенсивность гидростатического давления воды на глубине составит

Интенсивность гидростатического давления в связном грунте с учетом сцепления составит

Коэффициент активного давления связного грунта (второй слой) составляет

Интенсивность активного давления несвязного грунта на глубине составит

Коэффициент активного давления несвязного грунта (первый слой) составляет

Интенсивность активного давления несвязного грунта в связном грунте на глубине 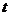составит

Интенсивность активного давления связного грунта на глубине 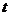составит

Интенсивность сцепления грунта со шпунтом, для активного давления, составляет

Интенсивность пассивного давления грунта на глубине 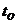составит

Коэффициент пассивного давления составляет

Интенсивность сцепления грунта со шпунтом, для пассивного давления составит

Уравнение устойчивости:

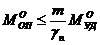(относительно точки «О»)

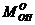¾ момент опрокидывающих сил относительно точки «О»

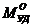¾ момент удерживающих сил относительно точки «О»

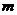¾ коэффициент условия работы,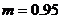

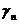¾ коэффициент надежности по назначению,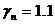

Рассматриваем устойчивость стенки против опрокидывания поворотом стенки относительно оси, расположенной на глубине 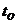ниже дна котлована (точка «О» на рис. 5.2, А).

Опрокидывающие силы: 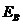, , 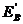, , 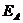принимается с коэффициентом надежности по нагрузке 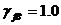и .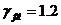

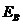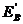Равнодействующие гидростатического давления и , действующие на стенку составляют:

тс

Равнодействующие активного давления несвязного грунта 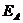, , действующие на стенку составляют

тс

тс

Равнодействующая активного давления грунта с учетом сцепления с внешней стороны, действующего на стенку определяется как совокупность сил

Равнодействующая активного давления грунта 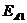составит

Равнодействующая сцепления шпунта с грунтом с внешней стороны 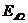составит

Момент от действия опрокидывающих сил 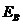, , 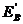, , 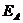относительно точки «О»:

Удерживающая сила: 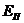, принимается с коэффициентом надежности по нагрузке .

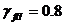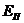¾ равнодействующая пассивного давления грунта с учетом сцепления со стороны котлована, действующего на стенку.

В связи со сложной формой эпюрой пассивного давления, разбиваем её на простые фигуры (треугольники и прямоугольник), у которых просто определять площадь и центр приложения равнодействующих сил. Получаем

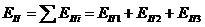
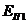¾ равнодействующая пассивного давления для треугольника высотой 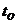и основанием равным . Получаем

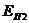¾ равнодействующая пассивного давления для треугольника высотой 1 м и основанием равным . Получаем

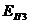¾ равнодействующая пассивного давления для прямоугольника высотой 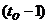м и основанием равным . Получаем

Момент от действия удерживающей силы относительно точки «О»:

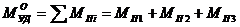
После подстановки величин моментов удерживающих и опрокидывающих сил в уравнение устойчивости, получаем неравенство:

Неравенство выполняется при м.

В рассмотренном случае, при глубине котлована 6.5 м, требуется заглубление стенки не менее 5.3 м. Рассмотрим возможность сократить величину погружения шпунта ¾ постановкой распорки внутри шпунтового ограждения.

Условия сооружения шпунтового ограждения прежние.

Распорку установим на глубине м от РУВ.

СХЕМА 2: принимаем к расчету шпунтовую стенку с одним ярусом крепления. Учитываем сцепление шпунта с грунтом (рис. 5.2, Б и В).

Значения действующих опрокидывающих и удерживающих сил будем принимать равными из схемы 1 (рис. 5.2, А).

Уравнение устойчивости:

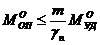(относительно точки «О»)

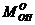¾ момент опрокидывающих сил относительно точки «О»

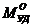¾ момент удерживающих сил относительно точки «О»

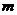¾ коэффициент условия работы,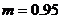

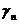¾ коэффициент надежности по назначению,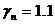

Рассматриваем устойчивость стенки против опрокидывания поворотом стенки относительно оси, расположенной в месте установки распорки (точка «О» на рис. 5.2, Б).

Момент от действия опрокидывающих сил 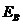, , 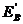, , 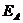относительно точки «О»:

Момент от действия удерживающей силы 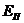относительно точки «О»:

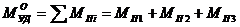
После подстановки величин моментов удерживающих и опрокидывающих сил в уравнение устойчивости, получаем неравенство:

Неравенство выполняется при м.

Минимальная глубина погружения шпунта с одним ярусом крепления по схеме 2 составляет 1.1 м.

Таким образом, постановкой распорки можно уменьшить глубину погружения шпунта.

Расчет на прочность по схеме 2 (рис. 5.2, В).

Расчет на прочность стенки с распорным креплением.

Уравнение прочности: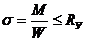

В расчете рассматривается 1 пог.м. поперечного сечения шпунта. Расчет выполняется по максимальному моменту, действующему в шпунте на 1 пог.м.

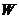¾ момент сопротивления 1 пог.м. поперечного сечения шпунтовой стенки.

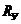¾ расчетное сопротивление металла изгибу по пределу текучести (по СНиП 2.05.03-84*).

При марке стали 15ХСНД расчетное сопротивление изгибу 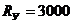кгс/см².

Рассматриваем балку на двух опорах с расчетным пролетом (рис. 5.2, В): опоры поставлены в месте установки распорки крепления (точка «О») и на половине глубины погружения шпунта (точка «В»). Длина расчетного пролета составляет

м

Давление воды и грунта, действующие на стенку ниже глубины , не учитывают. Изгибающий момент в сечении стенки, расположенном в пролете, допускается принимать равным:

0.75 ¾ коэффициент, учитывающий перераспределение давления грунта

Опорные реакции и определены от действующих сил (рис. 5.2, В).

тс тс

Максимальный действующий на стенку момент определим методом сечений.

тсм тсм тсм

Максимальный момент получен в точке 1:

тсм.

Находим требуемый момент сопротивления пог.м. стенки

см³

По требуемому моменту сопротивления 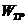выбираем по сортаменту тип шпунта с ближайшим большим моментом сопротивления:

шпунт ШК-2 с см³

Проверка выполняется.

Расчет распорки. Расчет распорки в точке О.

Давление стенки на распорку определяем по формуле

¾ интенсивность давления грунта на стенку.

Поскольку при расчетах распорки на устойчивость принимается 1 пог.м. ширины стенки, интенсивность давления определяется по формуле

тс/п.м.

, ¾ пролеты обвязки слева и справа от рассматриваемой распорки.

Примем м, тогда

тс.

В качестве распорки принимаем бревно Æ22 см ( см²) и м.

Имеем уравнение прочности

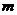¾ коэффициент, учитывающий понижение расчетного сопротивления для древесины сосны 2^го сорта,

¾ расчетное сопротивление изгибу элементов из бревен естественной коничности, кгс/см²

¾ коэффициент продольного изгиба.

Для определения вычисляем гибкость

Коэффициент продольного изгиба

Получаем

Проверка выполняется.

Таким образом,

· шпунтовое ограждение рекомендовано устраивать с одним ярусом крепления из шпунта ШК-2, забиваемого на глубину 1.1 м

· распорки из бревна Æ 22 см рекомендовано устанавливать на глубине 1.5 м от РУВ с шагом между ними 2.5 м.

Пример 3