Предельная чувствительность усилителя сигналов

Для колебательного контура

LCR – колебательный контур; У – усилитель.

Тепловое хаотическое движение электронов в резисторе R создает кратковременный ток, конденсатор заряжается, в контуре возникают колебания. Беспорядочные усиленные сигналы поступают на осциллограф.

Найдем флуктуацию напряжения на входе усилителя. Дисперсия напряжения связана с дисперсией заряда на конденсаторе

.

Конденсатор – одномерная система с энергией , что соответствует

, , ,

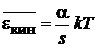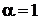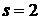тогда средняя тепловая энергия

, ,

.

Чем меньше электроемкость колебательного контура, тем больше флуктуация напряжения на конденсаторе.

Для колебательного контура ширина частотной полосы

и реактивное сопротивление на резонансной частоте

.

При согласованной нагрузке

,

где – входное сопротивление усилителя, тогда

,

,

и флуктуация напряжения

. (П.4.1)

Для приемника с полосой пропускания Dn = 10 кГц, входным сопротивлением R_у = 10 кОм, температурой Т = 290 К получаем dU = 1,6 мкВ, что ограничивает предельную чувствительность усилителя.

Флуктуационная ЭДС активного сопротивления

Хаотические тепловые движения электронов в проводнике вызывают коллективные перемещения электронов. Возникают стоячие волны с узлами на концах проводника.

Тогда

, ,

λ – длина волны;

l – длина проводника;

– число полуволн;

y – смещение вдоль проводника электронного облака от равновесного положения.

Число волн в интервале частот (0,n), где ; V – скорость волны:

,

где учтены две проекции спина электрона.

Число волн в интервале частот dn

.

Волне соответствует гармонический осциллятор, тогда на каждое колебательное движение приходится тепловая энергия kT. Энергия волн

.

Время распространения волны по проводнику

,

тепловая мощность

.

Тепловая мощность связана с ЭДС законом Джоуля–Ленца

.

Для фурье-компоненты флуктуационной ЭДС на частоте n получаем формулу Найквиста

, (П.4.2)

полученную Гарри Найквистом в 1928 г.

При Т ~ 300 К ЭДС слабо зависит от частоты, спектр тепловых флуктуаций является «белым». Флуктуация напряжения на концах проводника

, (П.4.3)

где Dn – полоса частот, регистрируемая измерителем сигналов. Условие применимости классической теории

.

Молярная теплоемкость простого тела.

Закон Дюлонга и Пти

Кристаллическая решетка удерживает атомы в узлах потенциальным полем

.

Сравниваем с

, (2.38)

находим

, .

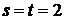Используем

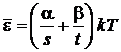, (2.39)

тогда средняя тепловая энергия атома

.

Внутренняя энергия моля

.

Молярная теплоемкость

(П.4.4)

– простые твердые тела обладают одинаковой, не зависящей от температуры молярной теплоемкостью – закон Дюлонга и Пти (1819 г.).