Распределение ТЕПЛОВОЙ энергии

По степеням свободы

Если степени свободы частицы входят в гамильтониан симметрично, то на каждую степень свободы приходится одинаковая тепловая энергия, обусловленная температурой.

Теорему предложил Дж. Уотерстон в 1845 г.,

количественное выражение дали Джемс Клерк Максвелл в 1860 г. и Людвиг Больцман в 1868 г.

Теорема применима для классических систем. Для квантовых систем теорема не выполняется.

Гамильтониан частицы

Рассмотрим гамильтониан со степенными зависимостями от координат и импульсов

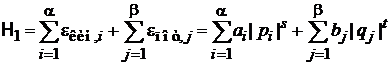, (2.38)

a – число активизированных степеней свободы кинетической энергии;

b – число активизированных степеней свободы потенциальной энергии;

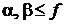– число степеней свободы частицы.

Средние значения

Кинетической и потенциальной энергии частицы

при температуре Т

Средняя энергия выражается через статистический интеграл частицы

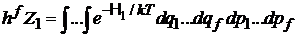. (2.19)

Интегрируем по 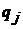, используя метод по частям:

, ,

, ,

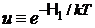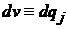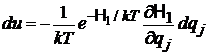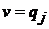тогда

.

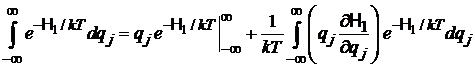Свободное слагаемое равно нулю за счет экспоненты. В результате

,

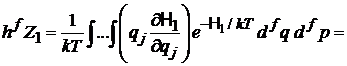
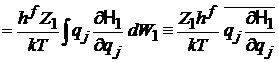где использовано каноническое распределение

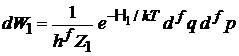(2.16)

и определение среднего

.

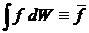В результате

,

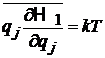и аналогично

.

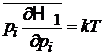Подставляем гамильтониан

,

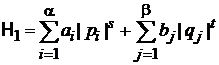получаем

,

.

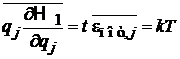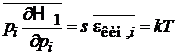Результаты не зависят от i и j, т. е. теорема о равном распределении тепловой энергии по степеням свободы выполняется. Учитываем

,

,

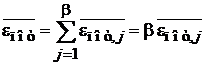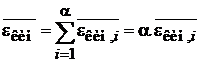тогда средние значения потенциальной, кинетической и полной энергий частицы

,

,

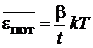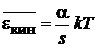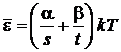. (2.39)

Примеры

1. Нерелятивистская свободная частица

, .

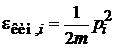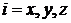Сравниваем с

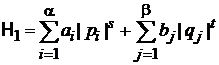, (2.38)

в виде

,

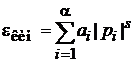находим

, ,

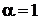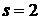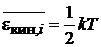. (2.40)

Для классического равновесного газа на каждую поступательную степень свободы частицы приходится тепловая кинетическая энергия .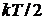

2. Линейный гармонический осциллятор

.

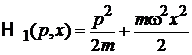Сравниваем с

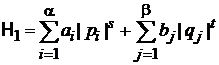, (2.38),

получаем

, ,

,

,

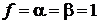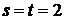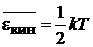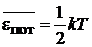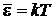
– на гармоническое колебательное движение приходится тепловая энергия kT.

НЕУСТРАНИМАЯ ПОГРЕШНОСТЬ

ИЗМЕРИТЕЛЬНОГО ПРИБОРА

Макрохарактеристики равновесной системы постоянны только в среднем. Колебания – флуктуации – вызваны хаотическими тепловыми движениями молекул.

Измерительное устройство испытывает тепловые колебания. Невозможно измерить физическую величину с точностью, меньшей амплитуды колебаний указателя прибора.

Оценим неустранимую погрешность прибора на примере весов, используя теорему о распределении энергии по степеням свободы.

Весы на основе упругой силы

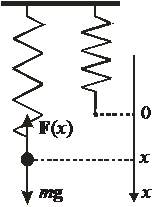
Весы – одномерная система. Потенциальная энергия

,

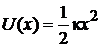x – отклонение указателя от положения равновесия ;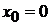

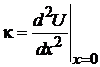– коэффициент жесткости.

Упругая возвращающая сила

.

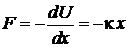Равновесие упругой и гравитационной сил

.

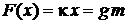Добавление массы 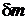изменяет показание весов на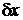

,

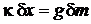тогда

,

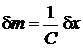где чувствительность

.

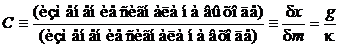Чем меньше коэффициент жесткости, тем выше чувствительность весов.

Средняя потенциальная энергия, связанная с одномерным тепловым хаотическим движением весов, согласно (2.39)

, , ,

.

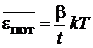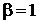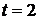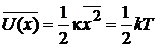Флуктуация показаний весов

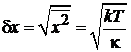
определяет наименьшую измеряемую массу

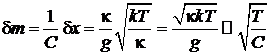
– неустранимая погрешность измерения.

Для уменьшения погрешности необходимо уменьшать температуру и увеличивать чувствительность весов.

Последнее требует уменьшениякоэффициента жесткости, который определяет частоту колебаний весов

,

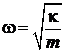нагруженных массой m. Используем 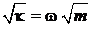, тогда относительная погрешность измерения

.

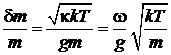При w = 10 Гц, Т = 290 К, m = 10^–3 г, получаем dm / m » 10^–5.