Свободная энергия и статистический интеграл

Из (2.24) получаем соотношение между свободной энергией F и статистическим интегралом Z

,

. (2.25)

Внутренняя энергияUи статистический интеграл

Внутренняя энергия является средним значением полной энергии системы

.

Из (2.16) и (2.17)

,

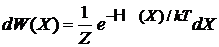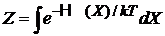находим

,

где использовано

.

Учитываем

,

получаем выражение внутренней энергии через статистический интеграл

. (2.26)

Уравнение Гиббса–Гельмгольца

Исключим статистический интеграл из (2.25) и (2.26), и найдем соотношение между внутренней энергией и свободной энергией, которое называется в термодинамике уравнением Гиббса–Гельмгольца.

Выражение

. (2.25)

в виде

подставляем в (2.26) и выражаем внутреннюю энергию через свободную энергию

(2.27)

– уравнение Гиббса–Гельмгольца. Следовательно, в (2.25) F – свободная энергия.

Из первого равенства в (2.27) получаем

.

Интегрируем

. (2.28)

В результате свободная энергия выражена через внутреннюю энергию.

Смысл свободной энергии

Является термодинамическим потенциалом – не зависит от пути перехода между начальным и конечным состояниями.

Является полным дифференциалом своих аргументов

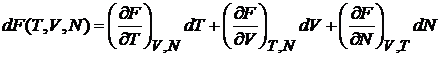. (2.30а)

В термодинамике известно соотношение

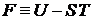. (2.31)

Берем дифференциал

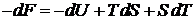. (2.31а)

Для равновесного, обратимого процесса используем

,

,

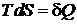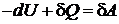тогда

,

и из (2.31а) при 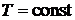получаем

.

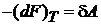Следовательно, свободная энергия является частью внутренней энергии, которая при изотермическом процессе переходит в работу.

Связанная энергия

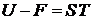
– часть внутренней энергии, которая при изотермическом процессе не может быть превращена в работу и выделяется в виде теплоты.

Понятия свободной и связанной энергий ввел Герман Гельмгольц в 1847 г.

Давление и статистический интеграл

Из первого начала термодинамики

,

и из определений энтропии и работы

,

,

находим

,

. (2.32)

Из (2.31а)

.

и из

, . (2.30а)

получаем

.

Тогда

, . (2.33)

Используем

, (2.25)

получаем

. (2.34)

Энтропия и статистический интеграл

Из (2.33) и (2.25)

. (2.35)

ПРИМЕР 1

N атомов идеального газа в объеме V при температуре Т совершают поступательные движения. Найти статистический интеграл, внутреннюю энергию и давление.

1. Статистический интегралатомов

Используем

,

.

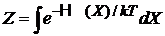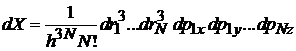Атомы совершают поступательные движения, тогда гамильтониан

.

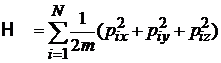Подстановка дает

,

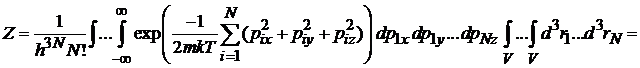
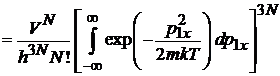где учтено

.

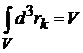Согласно

,

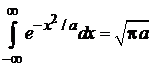интеграл в квадратных скобках равен 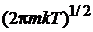. В результате статистический интеграл поступательного движения

,

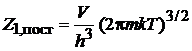. (П.3.1)

2. Внутренняя энергия

Используем

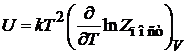. (2.26)

Из (П.3.1)

.

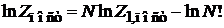По формуле Стирлинга

, ,

,

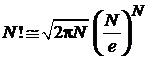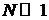тогда

.

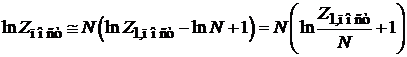С учетом (П.3.1)

,

получаем

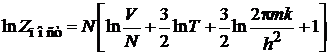. (П.3.1а)

Из

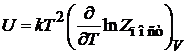(2.26)

получаем

,

.

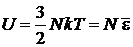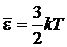3. Давление

Из (2.34) и (П.3.1а)

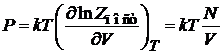
находим

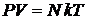– уравнение идеального газа,

, , .

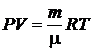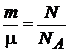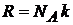ПРИМЕР 2

В двухатомной молекуле при температуре Т атомы совершают колебания с частотой ω. Найти статистический интеграл колебаний.

Молекулу считаем линейным осциллятором с гамильтонианом

.

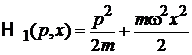Из

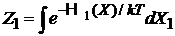, (2.17)

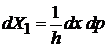
находим

.

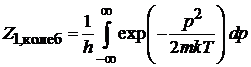
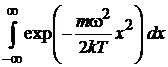Используя интеграл Пуассона

,

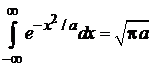для интегралов получаем

, .

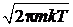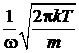В результате статистический интеграл колебательного движения молекулы

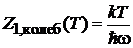. (П.3.5)

ПРИМЕР 3

Молекула массой m состоит из двух одинаковых атомов, находящихся на расстоянии 2r и вращающихся благодаря температуре Т. Найти статистический интеграл вращений.

Используем сферические координаты с центром в точке симметрии молекулы. На рисунке жирный круг – атом, второй атом в симметричной точке не показан.

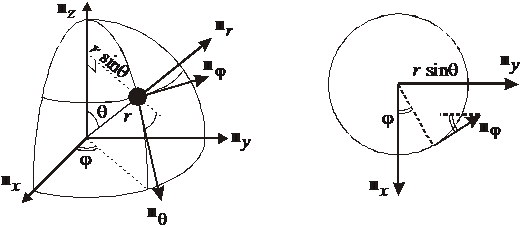
Атом вращается, изменяются углы φ и θ, угловая скорость связана с линейной скоростью

.

Линейную скорость атома разлагаем на составляющие:

· вдоль 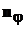со скоростью , где .

· вдоль 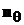со скоростью 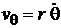, где .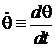

Кинетическая энергия двух атомов, выраженная через обобщенные координаты (φ, θ) и скорости 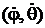, называется функцией Лагранжа

,

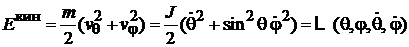где

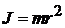
– момент инерции молекулы относительно прямой, перпендикулярной к оси молекулы и проходящей через центр масс.

Гамильтониан выражается через обобщенные импульсы 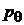и . Находим их из уравнения Лагранжа

.

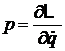Получаем

,

.

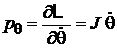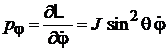Тогда

, .

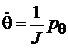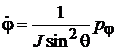Из

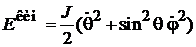
находим гамильтониан пространственного вращения

.

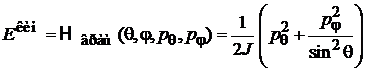Результат подставляем в

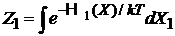, (2.17)

где

.

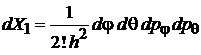Находим

.

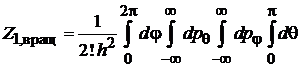
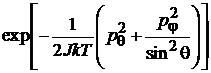Интегрируем вначале по j, затем по p_q, p_j и по θ.

С учетом

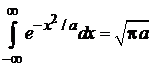
получаем

,

.

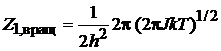
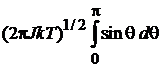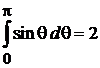Статистический интеграл вращательного движениямолекулы

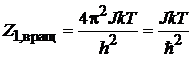. (П.3.6)