Фазовое пространство системы частиц

Микросостояние системыотображается точкой фазового пространства

,

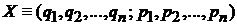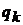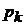где и – обобщенные координаты и импульсы частиц системы. С течением времени точка X движется согласно уравнениям Гамильтона

,

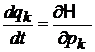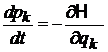. (2.1)

Гамильтониан 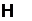– полная энергия системы, выраженная через координаты и импульсы частиц

.

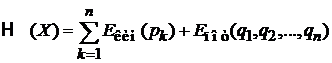Для нерелятивистской классической частицы массой m, движущейся вдоль оси k с импульсом 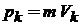, кинетическая энергия

.

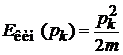Для консервативной системы полная энергия сохраняется

,

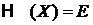и все микросостояния находятся на гиперповерхности в фазовом пространстве.

Найдем число измерений фазового пространства.

Число степеней свободы частицы

Число степеней свободы f есть число независимых координат, определяющих положение частицы в пространстве. Изменение координаты означает движение, тогда f – число независимых видов движений.

Атом в трехмерном пространстве имеет координаты (x,y,z) и . Изменение координат дает три поступательных движения. Вращательные движения не изменяют координат.

Двухатомная молекула. Два атома дают 6 координат. Если между атомами жесткая связь длиной l, тогда координаты связаны уравнением

.

Независимы координат. Их изменение дает 3 поступательных и 2 вращательных движения. Вращение вокруг оси y не изменяет координаты.

Упругая связь добавляет 2 степени свободы – кинетическую и потенциальную энергию колебаний, тогда для упругой связи .

Молекула из N атомов имеет координат.

При

3 степени свободы – поступательные движения,

3 – вращения.

Если связи жесткие, то .

– число связей между атомами.

Если связи упругие, то .

Например, для получаем .

«Вымерзание» степеней свободы

Молекула состоит из атомов, атом содержит ядро и электроны в оболочке. Эти структуры обладают внутренними степенями свободы. Обычно энергия связи структурных элементов молекулы велика по сравнению с тепловой энергией , поэтому внутренние степени свободы не активизируются и не проявляются.

При понижении температуры газа «вымерзают» колебательные движения молекулы, вызванные упругими связями, и для многоатомной молекулы с в трехмерном пространстве .

Далее «вымерзают» вращательные движения и .

При «вымерзают» поступательные движения, теплоемкость стремится к нулю согласно третьему началу термодинамики, и .

Число степеней свободы системы

Если число степеней свободы частицы f, то для N независимых частиц число степеней свободы:

,

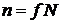и размерность фазового пространства системы .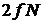

Число микросостояний

Элемент объема фазового пространства для системы с числом частиц N

.

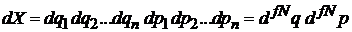При 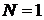, , 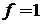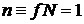единица измерения

,

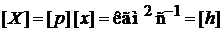где h – постоянная Планка.

При 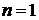соотношение неопределенностей Гейзенберга

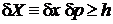
ограничивает снизу фазовый объем микросостояния величиной h. В 2n-мерном фазовом пространстве объем одного микросостояния 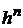. В результате число микросостояний равно безразмерному фазовому объему системы

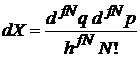. (2.2)

Множитель N! учитывает тождественность микрочастиц – их взаимная перестановка дает N! точек фазового пространства, отвечающих одному и тому же состоянию, которое должно учитываться однократно.

Вычисление объема

Идеальный свободный классический газ имеет 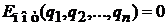и полную энергию

,

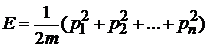тогда

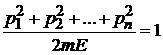
является уравнением сферы. Микросостояния с энергией Е находятся в импульсном пространстве на сфере радиусом .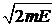

Объем и площадь n-мерной сферы

На основании размерности для объема n-мерной сферы получаем

,

.

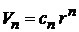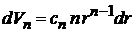Находим 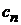, вычисляя по всему пространству интеграл:

.

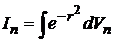В декартовых координатах

, ,

,

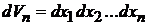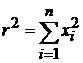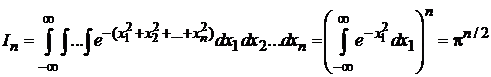где использован интеграл Пуассона

.

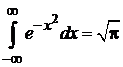В сферических координатах

,

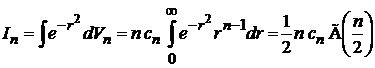где использовано

,

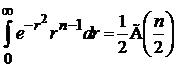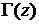– гамма-функция.

Сравнение выражений для 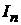дает

.

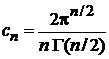Объем шара и шарового слоя

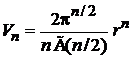, (П.2.1)

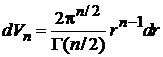. (П.2.2)

Площадь сферы

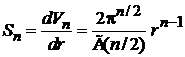, (П.2.3)

где

Г(n + 1) = n!,

Г(z + 1) = z Г(z),

,

, , ,

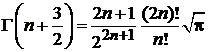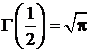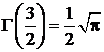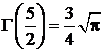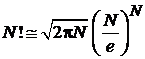, где .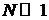

Для эллипсоида с полуосями 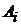уравнение

,

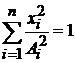объем

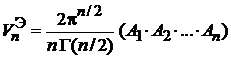. (П.2.1а)

Фазовая траектория

С течением времени система изменяет свое микросостояние за счет движения частиц, и точка X перемещается по фазовой траектории согласно уравнениям Гамильтона (2.1)

,

.
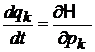
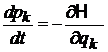