Теорема об изменении момента импульса механической системы.
Воспол теоремой об измен физических величин в механич системе 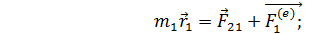 получим :
получим : 
 умножим первое уравнение слева векторно на
умножим первое уравнение слева векторно на  а второе уравнение слева векторно умножим на
а второе уравнение слева векторно умножим на  и в результате получим:
и в результате получим: 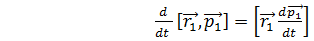 ;
; 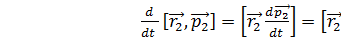
 ;
;  ;
; 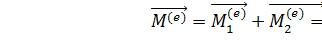 ;
; 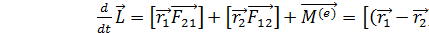 ;
;  ; тогда
; тогда  изменение момента импульса механич системы в единицу времени обусловлено действием момента внешних сил. Следствие 1: если отсутствует действие внешних сил:
изменение момента импульса механич системы в единицу времени обусловлено действием момента внешних сил. Следствие 1: если отсутствует действие внешних сил:  – закон сохранения момента импульса механич системы. Следствие 2: если
– закон сохранения момента импульса механич системы. Следствие 2: если  параллельны
параллельны  , тогда момент силы равен нулю:
, тогда момент силы равен нулю: 
Теорема об изменении кинетической энергии механической системы.

 умножим первое уравнение на
умножим первое уравнение на  а второе на
а второе на  и в результате получим:
и в результате получим: 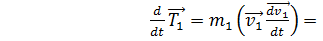 ;
; 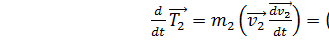 ; T=T1+T2-кинетическая энергия механической системы.
; T=T1+T2-кинетическая энергия механической системы. 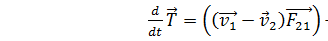 - теорема об изменении кинетической энергии. Изменение кинетичекой энергии в единицу времени механической системы обусловлено работой совершающей в единицу времени внешними и внутренними силами.
- теорема об изменении кинетической энергии. Изменение кинетичекой энергии в единицу времени механической системы обусловлено работой совершающей в единицу времени внешними и внутренними силами.  T1+T2)=
T1+T2)= 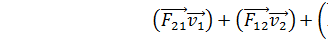 ;
; 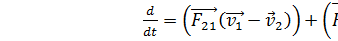 ; воспользуемся тем фактом,что силовые поля являя потенциальными полями, это значит что для всех полей выполн след соотнош:
; воспользуемся тем фактом,что силовые поля являя потенциальными полями, это значит что для всех полей выполн след соотнош:  ;
;  ;
;  ;
; 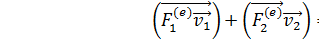 (
(  =
= 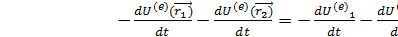 , -где
, -где  - энергия взаимодействия механической системы с внешним полем
- энергия взаимодействия механической системы с внешним полем  где
где  ;
; 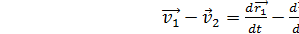 ;
; 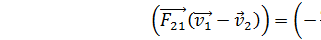 ;
; 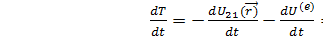 ; где
; где  - потенциальная энергия взаимод двух точек;
- потенциальная энергия взаимод двух точек;  - потенциальная энергия системы взаимод с внешним полем.
- потенциальная энергия системы взаимод с внешним полем.  ; W-полная энергия. W=T1+T2+T3+
; W-полная энергия. W=T1+T2+T3+ 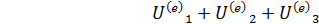 ; W=
; W= 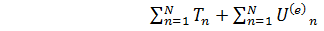 ; W=T+
; W=T+  ;
;  - закон сохранения энергии. Следствие 1: если внешнее поле отсутствует, то полная энергия будет состоять из: W=T+
- закон сохранения энергии. Следствие 1: если внешнее поле отсутствует, то полная энергия будет состоять из: W=T+  , при
, при  Следствие 2: если центр масс выразить через радиус:
Следствие 2: если центр масс выразить через радиус:
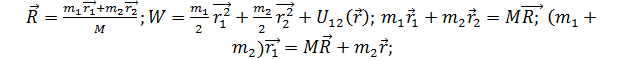
 ;
;  ;
; 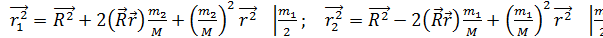 ; W=
; W= 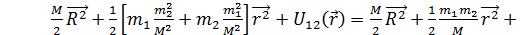 - полная энергия механической системы.
- полная энергия механической системы.  - кинетическая энергия механической системы, как целая, когда определяется движение центра масс механической системы.;
- кинетическая энергия механической системы, как целая, когда определяется движение центра масс механической системы.;  - приведенная масса. Кинетическая энергия механической системы, как материальная точка с приведенной массой
- приведенная масса. Кинетическая энергия механической системы, как материальная точка с приведенной массой  и относительной скоростью
и относительной скоростью 
 - потенциальная энергия.
- потенциальная энергия.
Вопрос
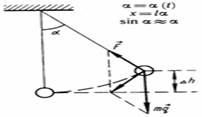
Будем рассматривать движение маятника при условии, что угол отклонения мал, тогда, если измерять угол в радианах, справедливо утверждение: На тело действуют сила тяжести и сила натяжения нити. Равнодействующая этих сил имеет две составляющие: тангенциальную, меняющую ускорение по величине, и нормальную, меняющую ускорение по направлению (центростремительное ускорение, тело движется по дуге).Т.к. угол мал, то тангенциальная составляющая равна проекции силы тяжести на касательную к траектории:  Угол в радианах равен отношению длины дуги к радиусу (длине нити), а длина дуги приблизительно равна смещению (x »s):
Угол в радианах равен отношению длины дуги к радиусу (длине нити), а длина дуги приблизительно равна смещению (x »s):  Сравним полученное уравнение с уравнением колебательного движени
Сравним полученное уравнение с уравнением колебательного движени 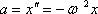
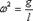
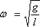
 Аналогичные вычисления можно проделать с помощью закона сохранения энергии. Учтем, что потенциальная энергия тела в поле тяготения равна
Аналогичные вычисления можно проделать с помощью закона сохранения энергии. Учтем, что потенциальная энергия тела в поле тяготения равна 
 а полная механическая энергия равна максимальной потенциальной или кинетической:
а полная механическая энергия равна максимальной потенциальной или кинетической:  Запишем закон сохранения энергии и возьмем производную от левой и правой частей уравнения:
Запишем закон сохранения энергии и возьмем производную от левой и правой частей уравнения: 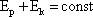 Т.к. производная от постоянной величины равна нулю, то
Т.к. производная от постоянной величины равна нулю, то  Производная суммы равна сумме производных:
Производная суммы равна сумме производных: 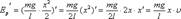
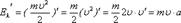
Следовательно

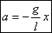
12 . Описание упругих колебаний материальной точки на основании 2-го закона Ньютона и закона сохранения энергии.  ;
;  ;
; 
 механ.Ньютона
механ.Ньютона 
 ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  .
.  ;
;  ;
;  ;
;  ;
;  -полная энергия;
-полная энергия;  =
=  - уравнение движения ;
- уравнение движения ;  ;
;  ; y=
; y=  dy=dz;
dy=dz;  ; C =-2
; C =-2  ;
;  ;
; 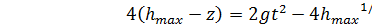 ;
;  ;
;
13.Связи. Уравнения связей.  -уравнение связи ;Связь– это совокупность тел огранич.движение определенного тела. Связи кот. огранич.движение тел описываются аналитическими ур-ями кот. наз.ур-ями связи. Рассмотрим движ. Одной мат.т.движ. кот.ограничена связеми. f(
-уравнение связи ;Связь– это совокупность тел огранич.движение определенного тела. Связи кот. огранич.движение тел описываются аналитическими ур-ями кот. наз.ур-ями связи. Рассмотрим движ. Одной мат.т.движ. кот.ограничена связеми. f(  =0; где
=0; где  t-время,
t-время,  (
(  =0,
=0,  (
(  =0,
=0,  (
(  =0,
=0,  (
(  =0; f(x)=0, f(x)=x-l; уравнение плоскости является связью
=0; f(x)=0, f(x)=x-l; уравнение плоскости является связью  -функции связи
-функции связи
Для круга 
Каждая определенная связь ограниченная движением мат.точки уменьшает число степеней свободы . стационарные связи –это такие связи ф-ии кот. явно не зависят от времени , в противном случае если ф-ии зависят от времени то она стационарная.В механ.использ. голономные и неголономныесвязи . Голономн.наз.связи кот. можно определить аналитич.ур-ями и эти ур-ия описываются опред. ур-ями поверхностей в противном случае связь явл.неголономной.силы кот.обусловленны действия связи наз.пассивными или реактивными силими. Активныминаз.силы кот вызывают ускорение мат. точек. Если мат.система состоит из N мат.точек 3N-P=r;Определение числа механ.системы с учетом связи огранич.движ.мех.системы. Виды перемещений: Действительные перемещения-это перемещение мат.точки под действием активных и пассивных сил. Возможные-это перемещ.кот.огран.связями действующ.на мат. точку или тело. Виртуальные –это вооброжаемые перемещ. кот. обусловл.действием активных и пассивных сил.
14.Элементы дифференцирования и варьирования в теоретической мех.  ; dz=vdt; z=z(t);
; dz=vdt; z=z(t);  ; Если в данный фиксированный момент времени переход от одной траектории к другой :
; Если в данный фиксированный момент времени переход от одной траектории к другой :  то эта операция перехода от одной траектории к другой близко расположенной относительно основной траектории наз.варьированием.
то эта операция перехода от одной траектории к другой близко расположенной относительно основной траектории наз.варьированием.  -варьирование преременных. С помощью операции варьирования определяется виртуальное варьирование. Если речь идет о вычислении вариации ф-ии зависящей от вариации
-варьирование преременных. С помощью операции варьирования определяется виртуальное варьирование. Если речь идет о вычислении вариации ф-ии зависящей от вариации  ;
;  ;
;  ;
;  (
(  =0,
=0,  ;
;  (
(  =
= 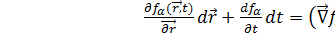 ;
;  (
(  =
=  ;
;  ;
;  =
=  ;
;  =
= 
15. Метод неопределенных множителей Лагранжа. Рассм. Мех. состоящую из N мат.т.на это на мех.систему наложено pсвязей(идеальных). r=3N-p Связи описываются ур-ями связи  ; все связи идеальны
; все связи идеальны  . Вычислим вариации ф-ции
. Вычислим вариации ф-ции  :
: 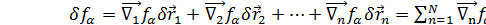 ; умножим ур-ние на
; умножим ур-ние на  и сложим все ур-ия :
и сложим все ур-ия :  ;
;  ; Если бы число степеней свободы мех. системы 3N то каждая
; Если бы число степеней свободы мех. системы 3N то каждая  было бы независимым и тогда выражение в квадратных скобках можно было бы прировнять к нулю, но число степеней свободы меньше 3N и равно 3N-p где р – число ур-ний связи.поэтому мы такого утверждения сделать не можем т.к.
было бы независимым и тогда выражение в квадратных скобках можно было бы прировнять к нулю, но число степеней свободы меньше 3N и равно 3N-p где р – число ур-ний связи.поэтому мы такого утверждения сделать не можем т.к.  неопределенные множители то мы подберем их таким образом что бы в каждом слогаемым выражение в квадратных скобках=0;
неопределенные множители то мы подберем их таким образом что бы в каждом слогаемым выражение в квадратных скобках=0;  из явного вида ф-лы
из явного вида ф-лы  связь реакции связи с ур-ями (функциями связи).
связь реакции связи с ур-ями (функциями связи).  ;
;  - ур-ние Лагранжа 1-го рода.
- ур-ние Лагранжа 1-го рода.
16. Ур-е Лагранжа 1-го рода.
Рассм. мех.сис-му, состоящ. из N материальн.точек. На эту мех.сис-му наложено р-связей идеальных. Число степеней свободы r = 3N-p.
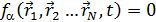 (8.1) a=1,2…p.
(8.1) a=1,2…p.

Вычислим теперь вариацию функций  ур-я (8.1):
ур-я (8.1):
d 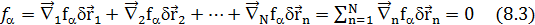
Умножим теперь кажд.ур-е (8.3) на множитель 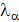 и сложим эти ур-я,тогда получ.:
и сложим эти ур-я,тогда получ.:
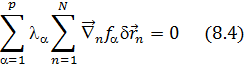
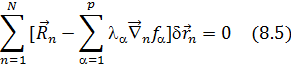
Если бы число степеней свободы мех.сис-мы было 3N, то каждая d 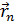 было бы независ. и тогда выраж-е в [ ] скобках можно было бы приравнять к 0, но число степеней свободы меньше 3N и равно 3N-p, где р- число ур-й связи, поэтому такого утверждения мы сделать не можем, однако, поскольку
было бы независ. и тогда выраж-е в [ ] скобках можно было бы приравнять к 0, но число степеней свободы меньше 3N и равно 3N-p, где р- число ур-й связи, поэтому такого утверждения мы сделать не можем, однако, поскольку 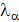 неопред.множители, то мы подберем их т.образом, чтобы в каждом слагаемом (8.5) выр-е в [ ] равнялись нулю. След-но из нашего утверждения следует, что
неопред.множители, то мы подберем их т.образом, чтобы в каждом слагаемом (8.5) выр-е в [ ] равнялись нулю. След-но из нашего утверждения следует, что
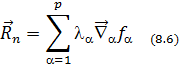
Из явного вида ф-лы (8.6) следует связь реакции связи с ур-ями (ф-циями) связи
 ур-е Д*аламбера.
ур-е Д*аламбера.
Если учтем ур-е (8.6), то получ.
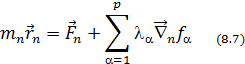
Это и есть ур-е Лагранжа 1-го рода.
Общее ур-е механики.

реакция связи, наз.идеальной для одной матер.точки,если выполн.ур-е:
( 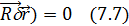

Принцип Д*аламбера:
При движ-ии матер.точки  сил действующих на матер.точку =0
сил действующих на матер.точку =0
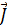 = -m
= -m 

Если ур-е (7.9) скалярно умножим на d  , то (
, то (  =0 (7.10), это ур-е наз.общим ур-ем механики для одной матер.точки.
=0 (7.10), это ур-е наз.общим ур-ем механики для одной матер.точки.
Для сис-мы состоящ.из n матер.точек принцип Д*аламбера будет записан так:
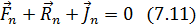 n=1,2…
n=1,2…
Если умножим (7.11) скалярно на d 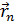 , а затем проссумируем.то получим:
, а затем проссумируем.то получим:
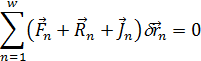
Если связь идеальна, то это ур-е запиш. В виде:
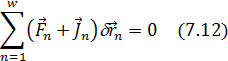
Общее ур-е механики
