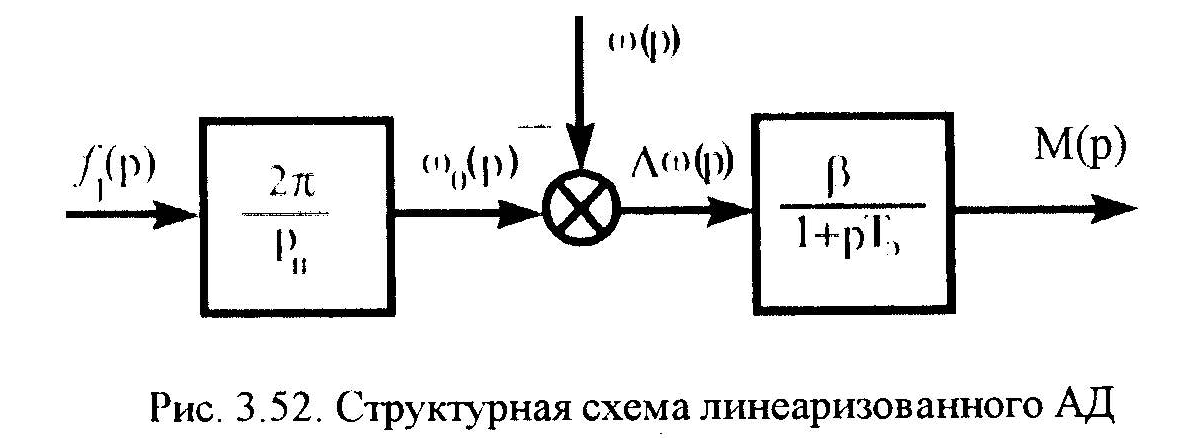
Структурная схема линеаризованного АД при питании от источника напряжения.

Для получения структурных схем и при векторном управлении АД используется математическая модель двухфазного АД в синхронно вращающихся осях x-y.

В векторной форме эта математическая модель соответствует (2.142) при 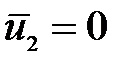, т.е.

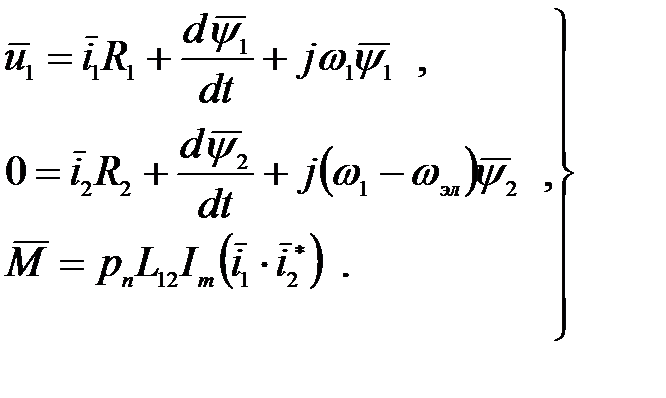(3.197)

При этом напряжения, токи и потокосцепления в системе координат x-y являются величинами постоянного тока. Система уравнений (3.197) может быть преобразована в систему уравнений, записанных в форме Коши (иногда называемую системой уравнений в пространстве состояния переменных) и разрешенных относительно потокосцеплений с добавлением уравнения движения электропривода:

При синусоидальном питании обмоток статора имеем

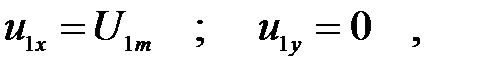
где U_1m – амплитуда синусоидального питающего напряжения.

Математическая модель (3.198), как и предыдущие модели АД, нелинейная, поскольку содержит произведения переменных: 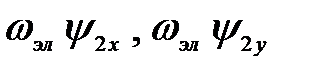, 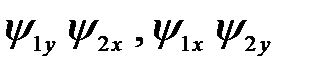. Связь выходных величин скорости и электромагнитного момента с входными – амплитудой напряжения и частотой, т. е. динамические свойства АД определяются на основе результатов компьютерного моделирования с учетом заданной величины статического момента.

В некоторых случаях АД работает при постоянном потокосцеплении y₁ статора, например, при набросе нагрузки. Если принять R₁ = 0 , y₁=const , то система (3.198) принимает вид:

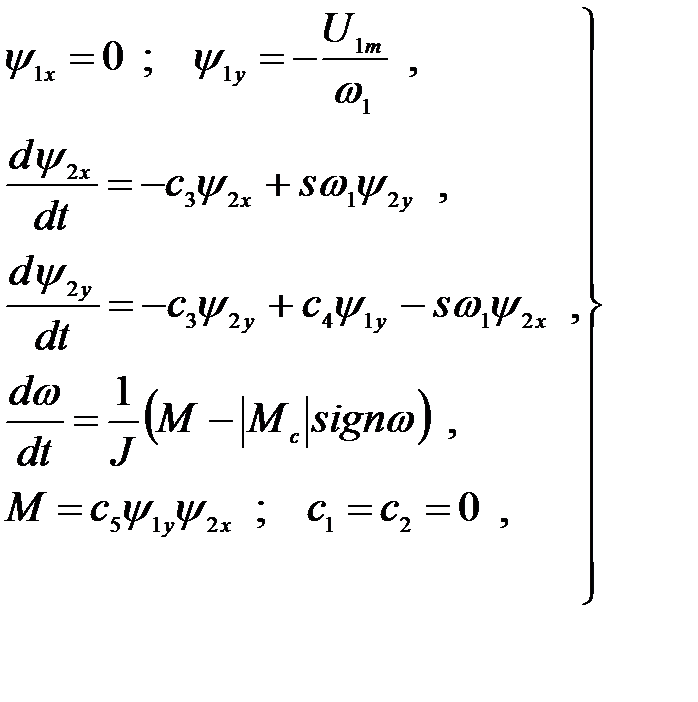(3.199)

где 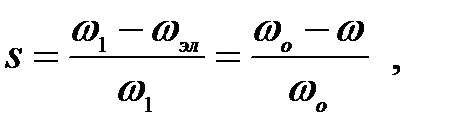(3.200)

s – скольжение АД,

w_о – синхронная угловая скорость АД.

Приняв

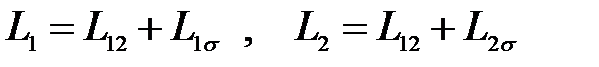(3.201)

и полагая L₁ » L₁₂ , получим:

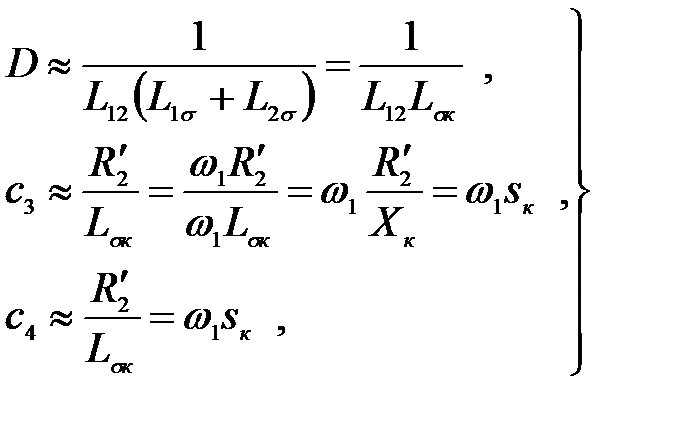(3.202)

где 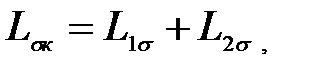(3.203)

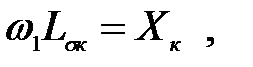(3.204)

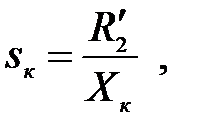(3.205)

L_sк – индуктивность короткого замыкания АД,

L_1s , L_2s - индуктивности рассеяния статора и ротора,

Х_к – индуктивное сопротивление короткого замыкания,

R¢₂ – приведенное к статору эквивалентное активное сопротивление фазы ротора,

S_к – критическое скольжение АД при R₁ = 0.

Уравнения электрического равновесия ротора в системе (3.199) можно представить в операторной форме

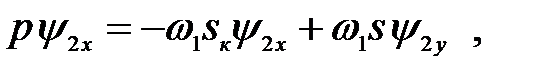(3.206)

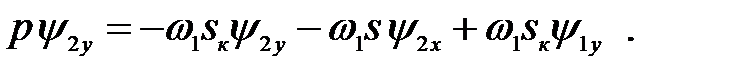(3.207)

Преобразовываем (3.206):

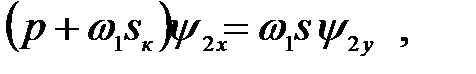
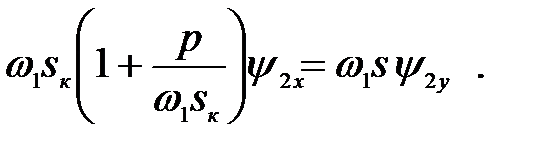(3.208)

Обозначим

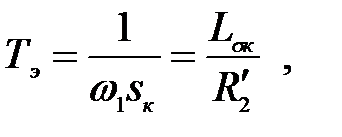(3.209)

тогда из (3.208) получаем

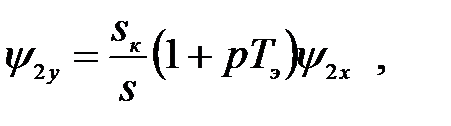(3.210)

где Т_э – электромагнитная постоянная времени АД.

Представляем (3.207) в виде

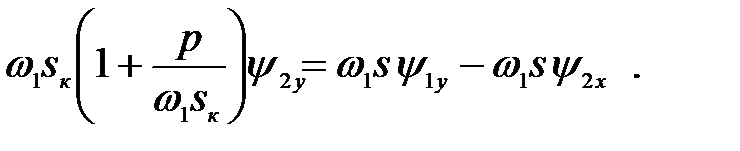(3.211)

Учитывая (3.209), находим

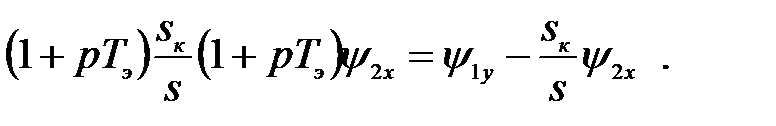(3.212)

Из (3.212) определяем

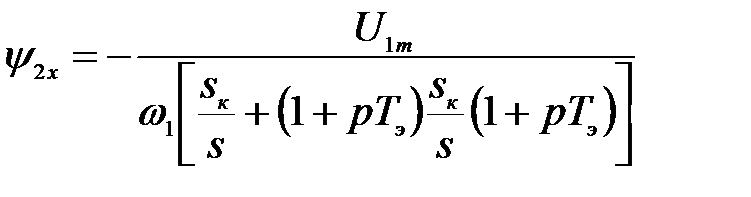(3.213)

и подставляем в уравнение электромагнитного момента системы (3.199), в результате получаем

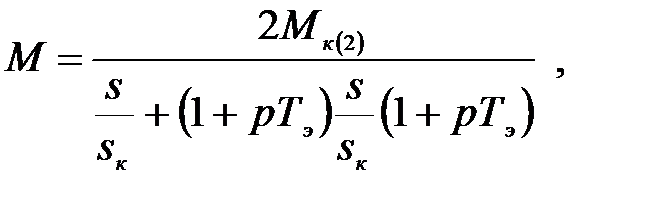(3.214)

где 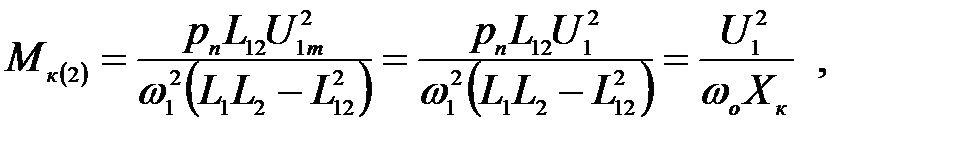(3.215)

М_к(2) – максимальный (критический) момент двухфазного АД, при R₁ = 0 ,

U₁ – действующее значение фазного синусоидального напряжения.

Для m – фазного АД критический момент при R₁ = 0 можно записать в виде:

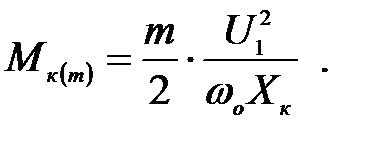(3.216)

Операторное уравнение (3.214) представляет собой динамическую механическую характеристику двухфазного АД. Если принять во внимание (3.216), то это будет уравнение динамической механической характеристики m – фазного АД. Представим это уравнение таким образом:

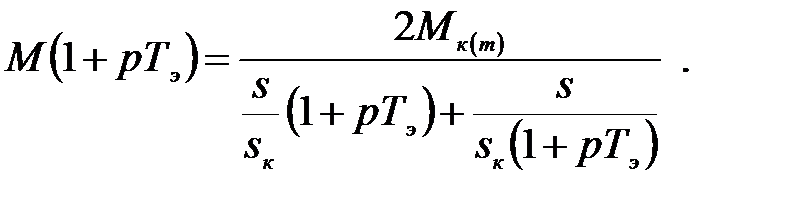(3.217)

При малых скольжениях можно принять 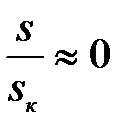и так как 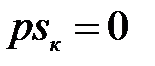, то (3.217) принимает вид

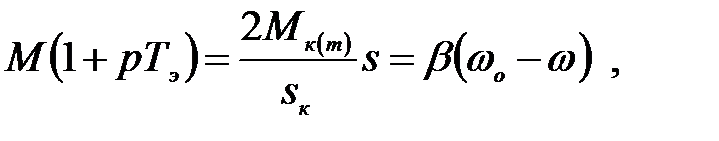(3.218)

где 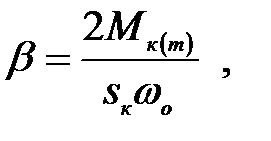(3.219)

b - модуль жесткости статической линеаризованной механической характеристики.

Операторному уравнению (3.218) соответствует структурная схема, показанная на рис.3.52.