Характеристики и свойства асинхронного двигателя при питании от источника тока.

Системы электропривода при переменной частоте тока статора и постоянной величине этого тока относятся к разомкнутым системам частотно-токового управления АД, которые находят применение в регулируемых электроприводах переменного тока (рис.3.63). В более сложных, замкнутых, системах частотно-токового управления устраняются недостатки, присущие разомкнутым системам. Поэтому представляет интерес выявить основные свойства разомкнутых частотно-токового управления АД.

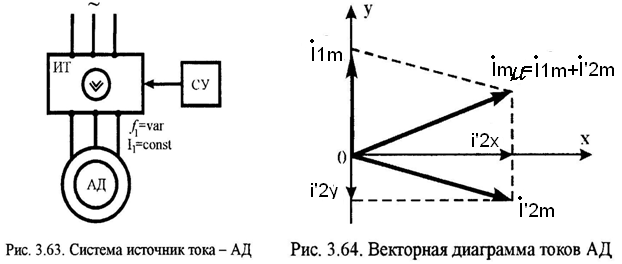
Для анализа воспользуемся синхронно вращающейся системой координат x-y. Направим вектор тока статора 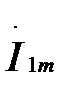вдоль положительного направления оси y (рис.3.64). Получаем векторную диаграмму токов двухфазного АД в системе координат x-y.

Уравнения двухфазного АД в этой системе координат имеют вид:

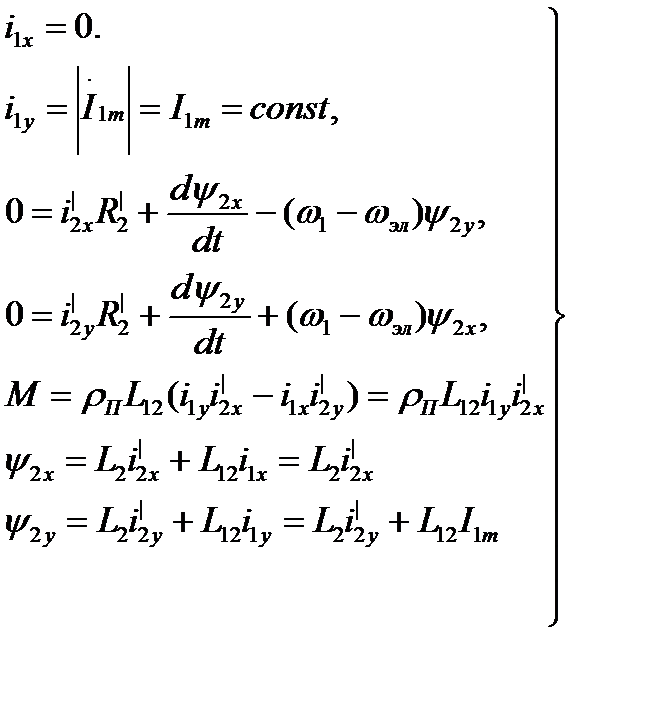(3.263)

Уравнения ротора АД записываем в операторной форме, выразив потокосцепления через токи:

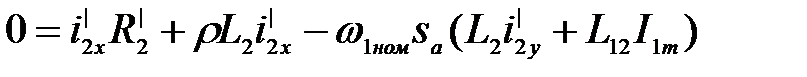(3.264)

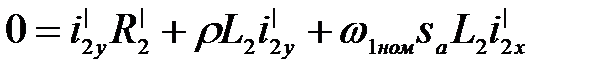(3.265)

где 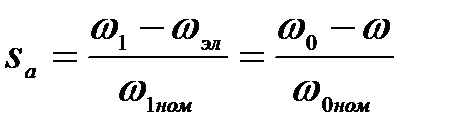(3.266)

s_a – абсолютное скольжение,

w_0ном – синхронная угловая скорость АД при номинальной частоте f_1ном,

w₀ – синхронная угловая скорость АД при текущей частоте f₁.

Представим (3.264) в виде:

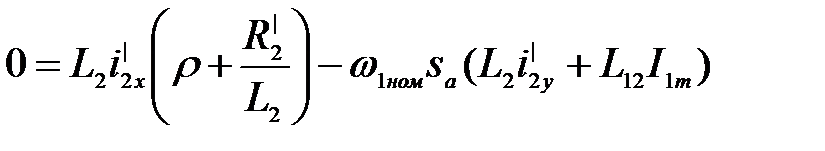(3.267)

Преобразуем отношение

,

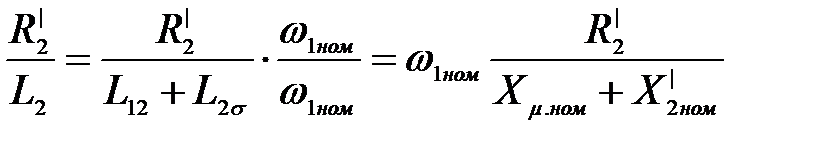где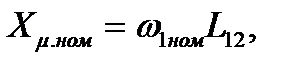

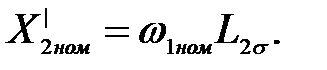
Обозначим

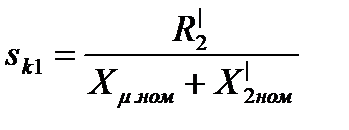, (3.268)

тогда

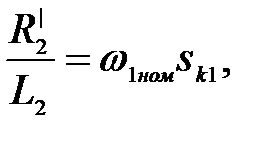(3.269)

где s_к1 – критическое скольжение АД при питании от источника тока.

Теперь (3.267) можно представить таким образом

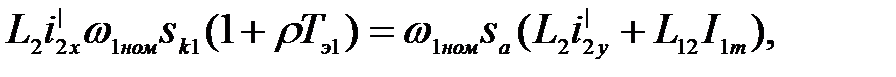(3.270)

где 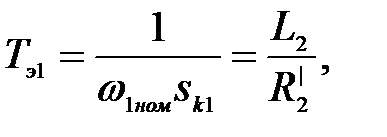(3.271)

T_э1 – электромагнитная постоянная времени АД при питании от источника тока.

Из (3.270) определяем

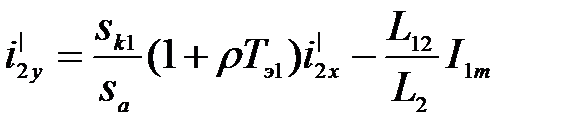(3.272)

Записываем (3.265) в виде

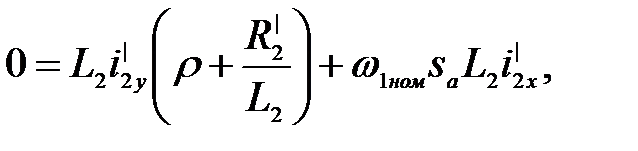(3.273)

что с учетом (3.271) и (3.268) приводит к выражению:

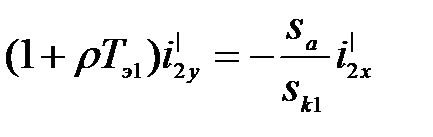(3.274)

Подставляем (3.272) в (3.274):

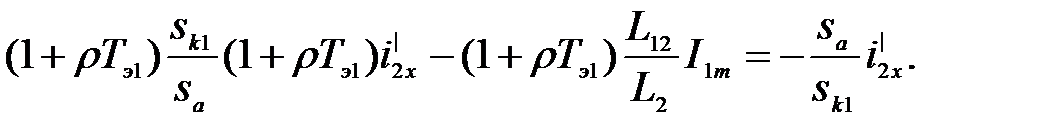(3.275)

Примем во внимание, что

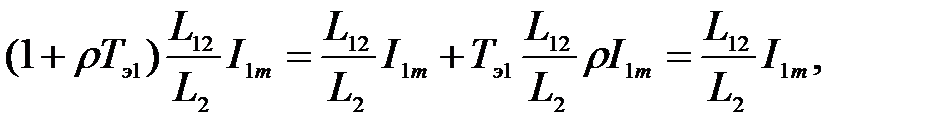(3.276)

так как 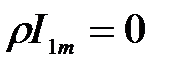. Из (3.275) с учетом (3.276) получаем

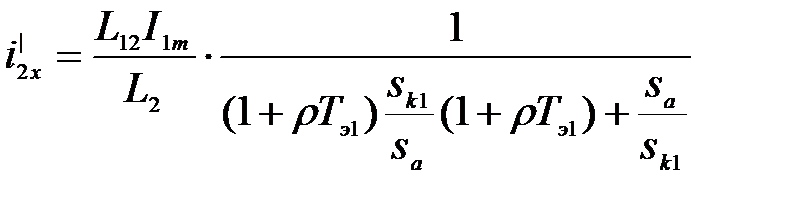(3.277)

Электромагнитный момент АД

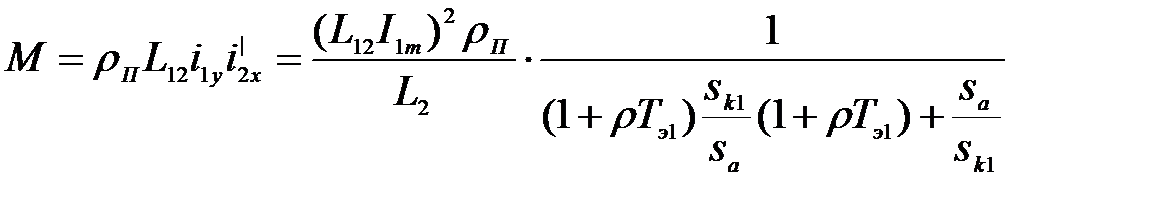(3.278)

Преобразуем:

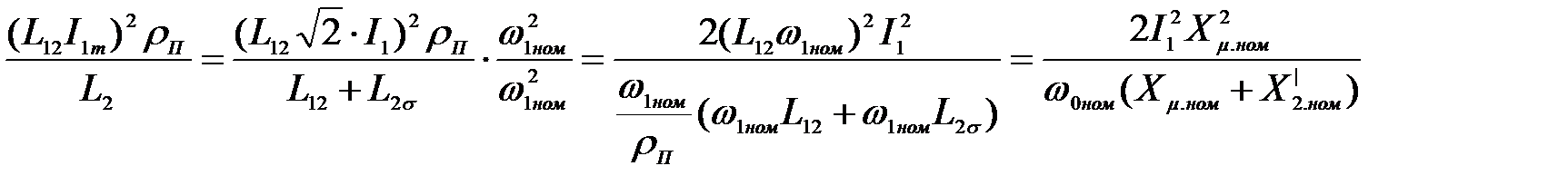(3.279)

Обозначим

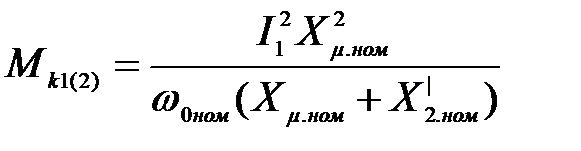(3.280)

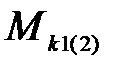- критический момент двухфазного АД при питании от источника тока.

Для m-фазного АД

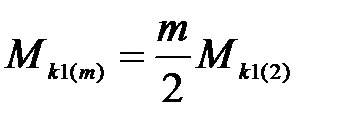(3.281)

После введения 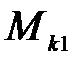получаем уравнение динамической механической характеристики АД при питании от источника тока:

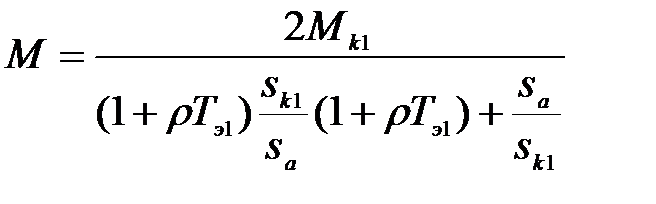(3.282)

Представим это выражение в виде

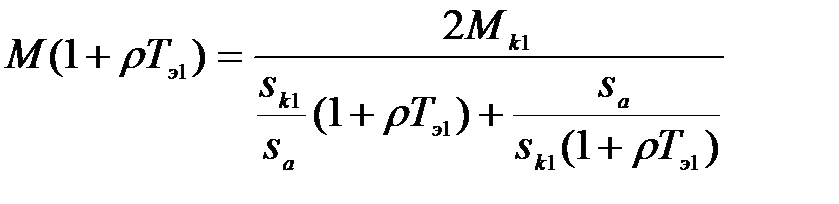(3.283)

При малых значениях абсолютного скольжения s_a можно принять 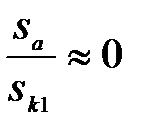, тогда

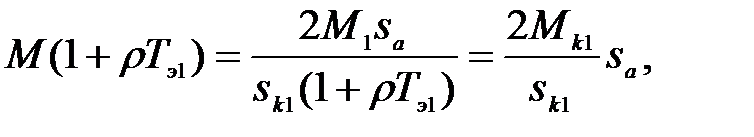(3.284)

так как

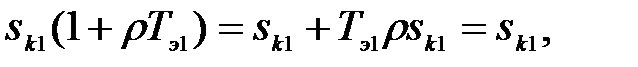
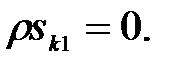
Подставив (3.266) в (3.284), получаем операторное уравнение

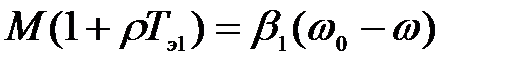, (3.285)

где 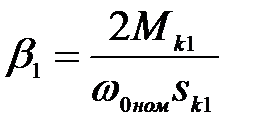, (3.286)

b₁ – модуль жесткости линеаризованной механической характеристики АД при питании от источника тока.

Операторному уравнению (3.285) соответствует структурная схема, приведенная на рис.3.65 (нету).

Для установившегося режима работы r=0. Принимая 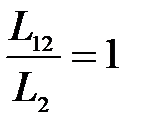, на основании (3.277) и (3.272) получаем составляющие тока ротора АД для установившегося режима:

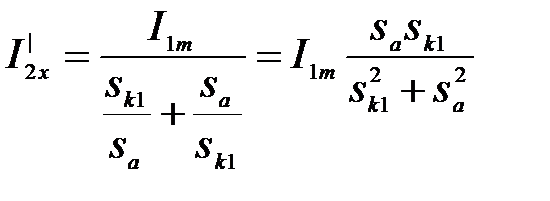, (3.287)

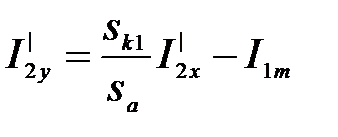. (3.288)

Учитывая составляющие тока статора I_1x=0. I_1y=I_1m, определяем амплитудное значение намагничивающего тока (см. рис.3.64):

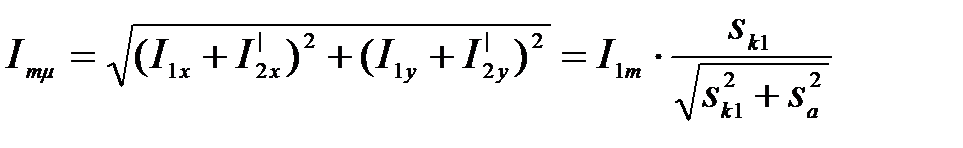(3.289)

Следовательно, с увеличением нагрузки АД, т.е. s_a, намагничивающий ток I_m (действующее значение) и создаваемый им магнитный моток будут уменьшаться. Наибольшее значение намагничивающего тока и магнитного потока будет при s_a=0 (рис.3.66). В широком диапазоне нагрузок АД при питании от источника тока работает с переменным магнитным потоком. Изменяющийся ток I_m приводит к переменной величине индуктивного сопротивления намагничивающего контура

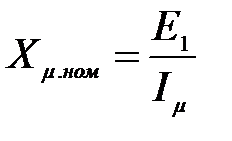(3.290)

в соответствии с кривой намагничивания (рис.3.67).

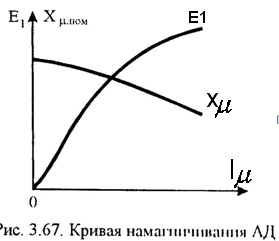
Уменьшение X_m.ном c увеличением I_m с способствуем снижению критического момента М_к1, который оказывается меньше критического момента М_ке на естественной характеристике АД. Чтобы получить М_к1= М_ке, необходимо увеличить ток статора до значений 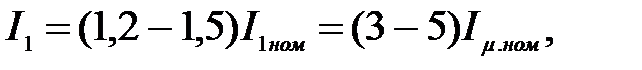что недопустимо как по условиям нагрева, Так и по условиям насыщения магнитной системы. Как следует из (3.209) и (3.271), ,

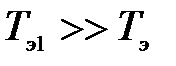поскольку .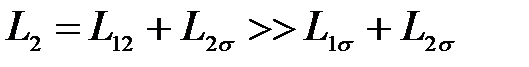

Статические механические характеристики АД получаются из (3.282) при r=0:

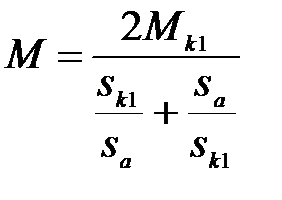(3.291)

Угловая скорость ротора АД определяется выражением

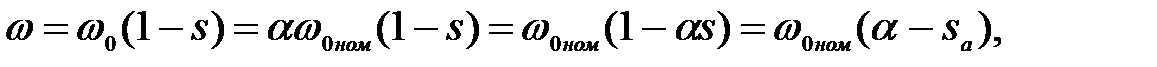(3.292)

где 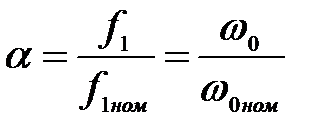(3.293)

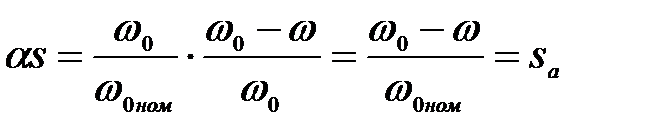(3.294)

обозначив

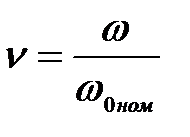, (3.295)

из (3.292) получим важное соотношение безразмерных величин

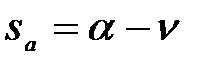, (3.296)

характеризующих работу АД при переменной частоте. Теперь уравнения механических характеристик АД (3.291) при различных частотах a можно записать в таком виде:

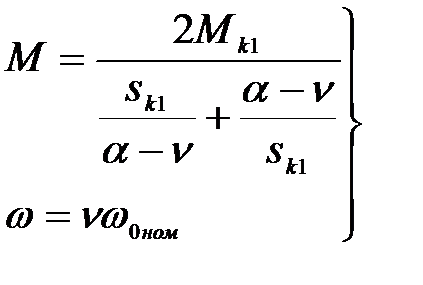(3.297)

Все эти характеристики при одном значении электромагнитного момента имеют одинаковую жесткость. Поэтому графически это будет семейство подобных (конгруэнтных) кривых(рис.3.68).

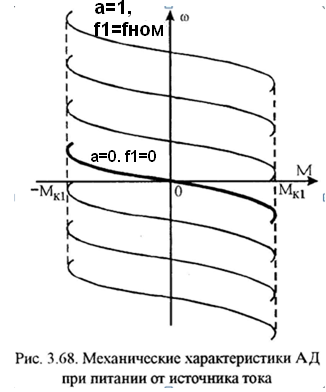
Характеристика, соответствующая a=0 (f₁=0), получается при питании АД от источника постоянного тока.