Обобщенные математические модели механической части эп

В общем случае механическую часть электропривода можно представить в виде n сосредоточенных масс, соединенных между собой упругими элементами. При этом у отдельных элементах передачи возможны люфты (Рис.1.5). Все параметры такой модели механической части приводятся к одной оси, чаще всего к валу электродвигателя. Так как люфты в передаче приводят к нелинейным уравнениям в механической части, то ими часто пренебрегают.

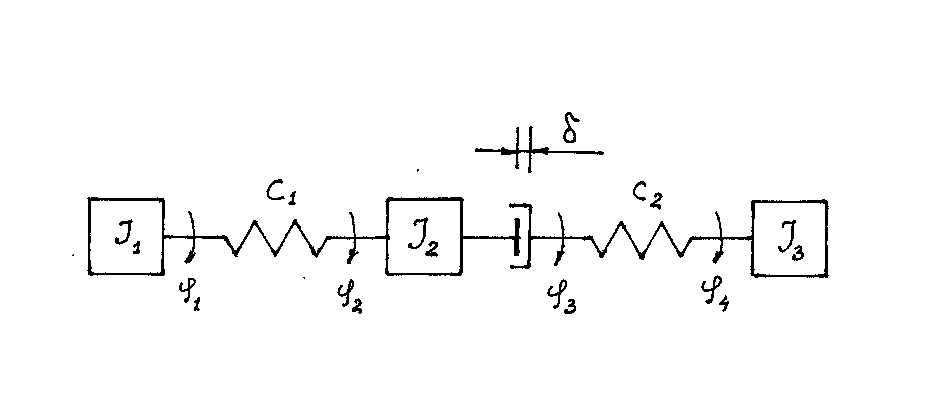
В модели механической части электропривода выделяют действующие силы непотенциального характера (электромагнитные силы и моменты, силы сопротивления, обусловленные выполняемой работой), силы упругости и диссипативные силы, вызванные свойством механической части рассеивать часть полной механической энергии внутри себя. Диссипативные силы связаны с наличием вязкого трения и упругого механического гистерезиса.

Движение представленной модели n-массовой системы описывается системой уравнений Лагранжа второго рода

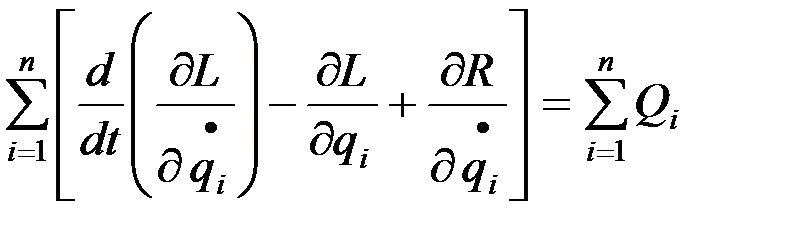
где

L – функция Лагранжа, т.е.

L=W_к-W_n , (1.12)

W_к , W_n – кинетическая и потенциальная энергия системы,

R – функция Рэлея (диссипативная функция), определяемая как

R= 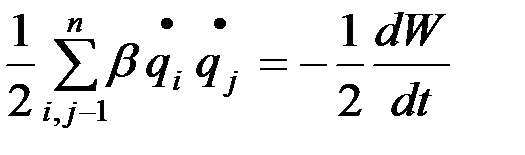, (1.13)

W – полная механическая энергия системы, 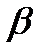– коэффициент, 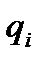– обобщенная координата i-й степени свободы, 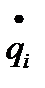– обобщенная скорость i-й степени свободы, 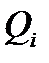– обобщенная сила, действующая на i-й степени свободы,t – время.

Поступательное перемещение s_М приводится к вращательному движению вала двигателя таким образом: j= s_Мr,

где r - радиус приведения.

Момент инерции J_м и жесткость кручения С_м механизма приводятся к валу двигателя в соответствии с выражениями:

, .

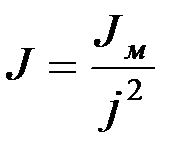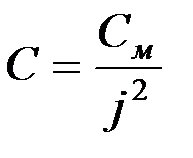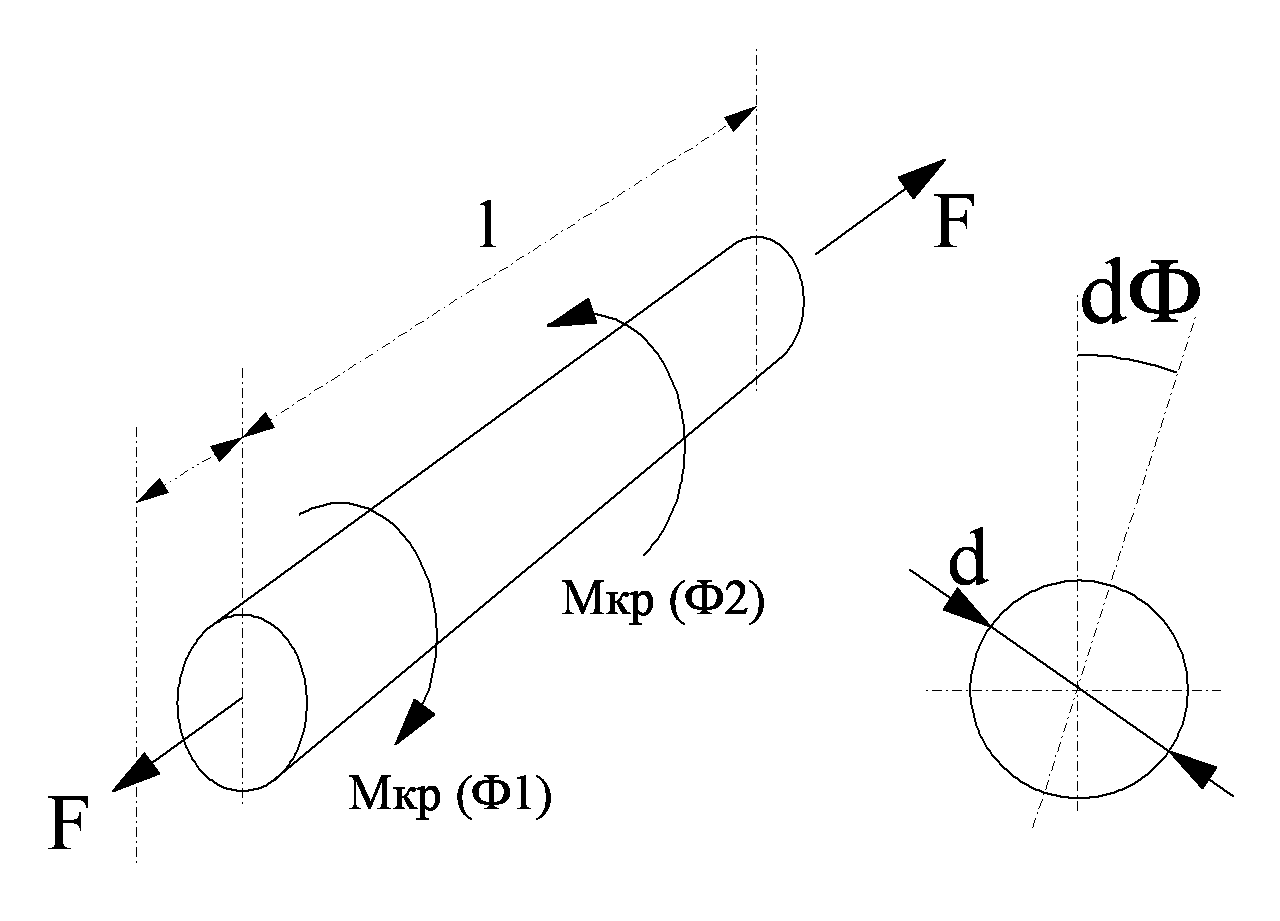
Коэффициент жесткости при кручении вала определяется выражением

,

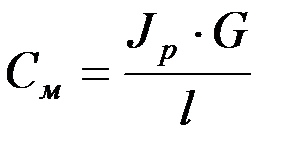где l – длинна вала, м.;

.

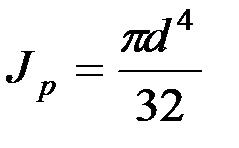J_p – момент инерции поперечного сечения, м ; G – модуль упругости при сдвиге, Па; d – диаметр поперечного сечения, м.

Поступательно движущаяся масса m определяет на валу двигателя эквивалентный момент инерции

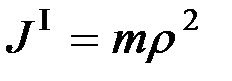
Аналогично рассчитывается эквивалентная жесткость 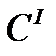,обусловленная линейной упругой деформацией на стороне механизма и своей величиной жесткости :

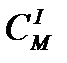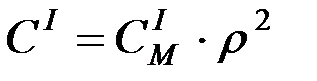
Коэффициент жесткости при линейной деформации (растяжение, сжатие) рассчитывается таким образом:

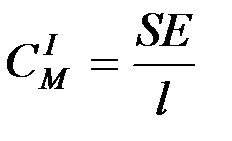
где S – площадь поперечного сечения, м ;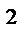

Е – модуль упругости растяжения или сжатия, Па;

l – длинна, подверженная растяжению или сжатию.

4. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И СТРУКТУРНАЯ СХЕМА ДВУХМАССОВОЙ МОДЕЛИ ЭП.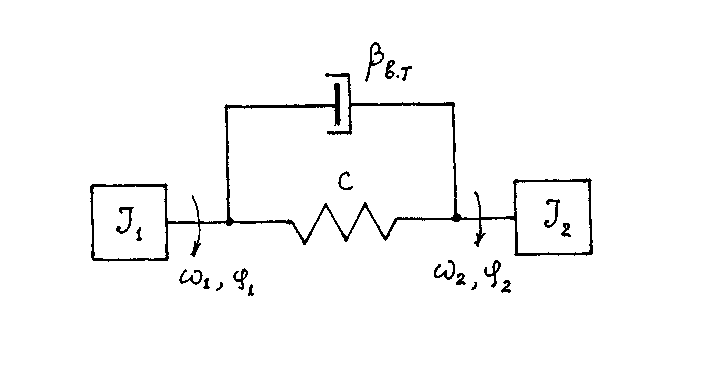

В связи с тем, что для электропривода наибольший интерес представляет вращение вала электродвигателя, с помощью которого осуществляется управление движением, и вала исполнительного механизма, осуществляющего технологическую операцию, n-массовую модель электропривода (1.11) преобразуют к эквивалентной модели двухмассовой системы.

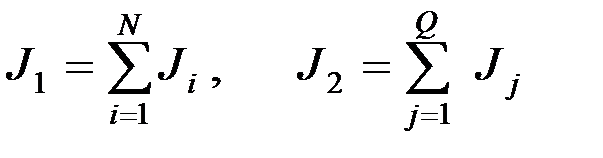
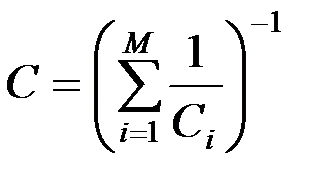
В результате получаем математическую модель эквивалентной двухмассовой системы:

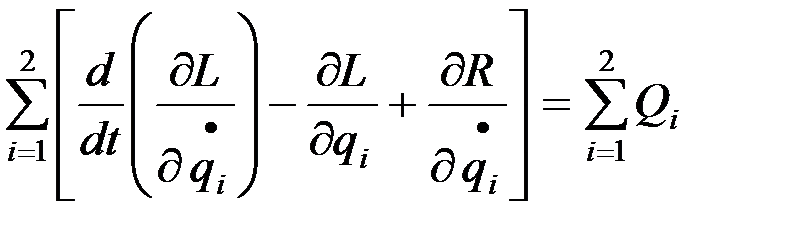где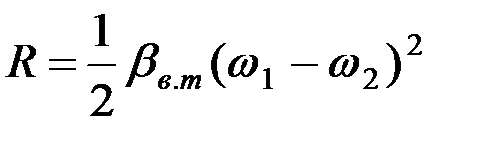

,

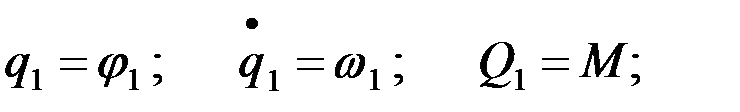
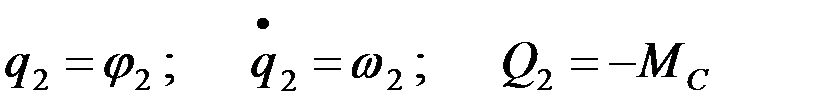j­₁, w₁, М – угол поворота, скорость и момент первой массы. Также и для второй тока место1 пишим 2.

дифференциально-интегральных уравнений:

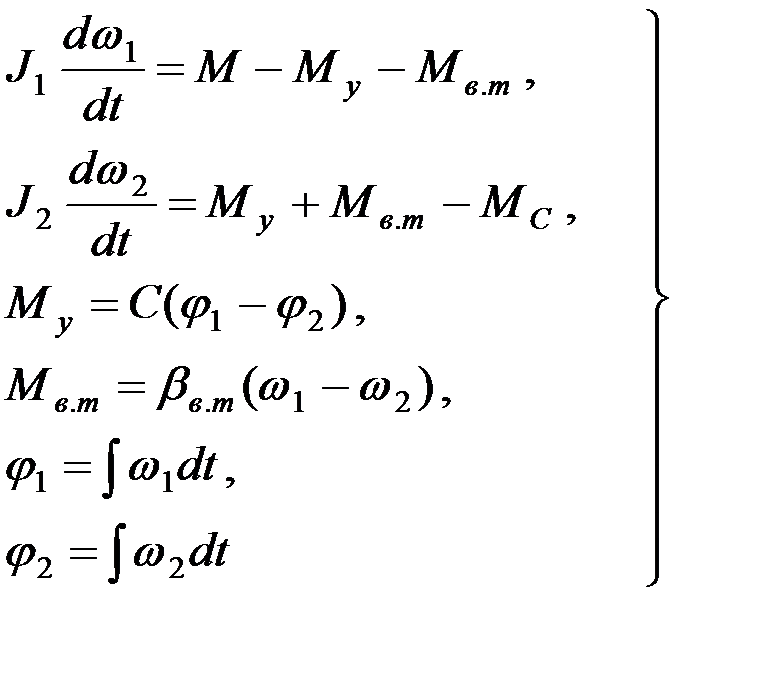
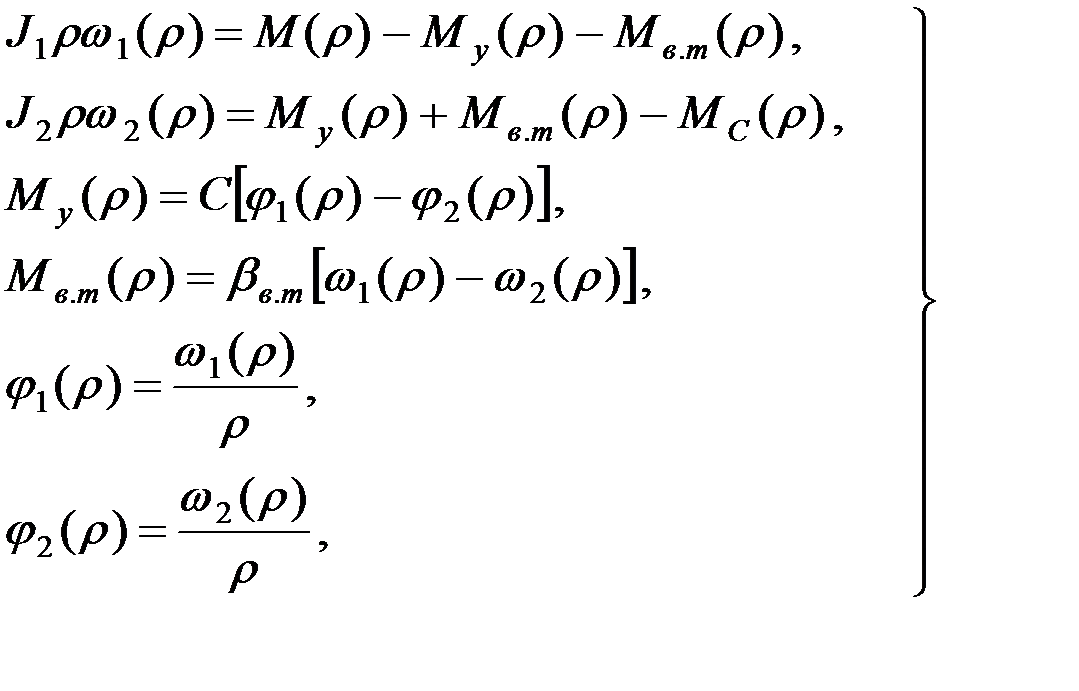
где М_у и М_в.т – упругий момент и момент вязкого трения,

М_С – статический момент на валу электродвигателя.

Система уравнений (1.26) является по существу “уравнением движения двухмассовой модели электропривода”. Эту систему уравнений можно записать в операторной форме.

где 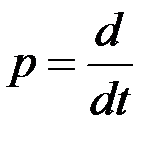– оператор дифференцирования,