Расчет МДС зубцовой зоны якоря
В зубцовой зоне якоря магнитный поток идет параллельными путями через соседние зубцовые деления,поэтому падение магнитного потенциалана всех зубцовых делениях будут практически одинаковыми. С учетом этого обстоятельства при расчете МДС зубцовой зоны якоря можно ограничиться расчетом МДС только для одного зубцового деления.
Обозначим через 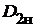 и
и 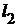 соответственно наружный диаметр якоря и длину пакета стали якоря.Магнитный поток
соответственно наружный диаметр якоря и длину пакета стали якоря.Магнитный поток 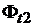 в воздушном зазоре, соответствующий одному зубцовому делению якоря
в воздушном зазоре, соответствующий одному зубцовому делению якоря 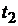 (рис. 1.6 и 1.7), будет равен
(рис. 1.6 и 1.7), будет равен
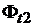 =
= 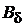
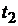
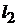 ; (1.18)
; (1.18)
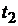 =
= 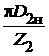 .
.
Предполагая, что весь магнитный поток 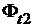 проходит полностью череззубец,определиммагнитнуюиндукцию
проходит полностью череззубец,определиммагнитнуюиндукцию 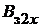 впроизвольном сечении
впроизвольном сечении 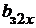 зубца по его высоте
зубца по его высоте 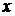 , считая от основания зубца
, считая от основания зубца
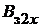 =
= 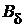
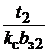 , (1.19)
, (1.19)
где 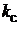 = 0,97 – коэффициент заполнения пакета якоря сталью. Из выражения (1.19) видно, что величина
= 0,97 – коэффициент заполнения пакета якоря сталью. Из выражения (1.19) видно, что величина 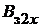 обратно пропорциональна ширине зубца, и в минимальном сечении зубца
обратно пропорциональна ширине зубца, и в минимальном сечении зубца 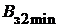 магнитная индукция в этом сечении зубца будем максимальной:
магнитная индукция в этом сечении зубца будем максимальной:
 =
= 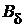
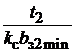 . (1.20)
. (1.20)
На рис. 1.6 и 1.7 представлены фрагменты зубцовойзоны якоря с пазами соответственно прямоугольной и овальной формы. Для пазов прямоугольной формы размер 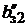 определяет минимальную ширину зубца, а для пазов овальной формыминимальная ширина зубца равна
определяет минимальную ширину зубца, а для пазов овальной формыминимальная ширина зубца равна 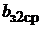 .
.
Подставляя в выражение (1.20) значения 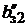 или
или 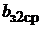 , можно вычислитьсоответствующее значение
, можно вычислитьсоответствующее значение  .
.
Возможны два случая расчета МДС зубцовой зоны якоря в зависимости от значения магнитной индукции  в минимальном сечении зубца
в минимальном сечении зубца 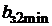 :
: 
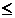 1,8 Тли
1,8 Тли  > 1,8 Тл.
> 1,8 Тл.
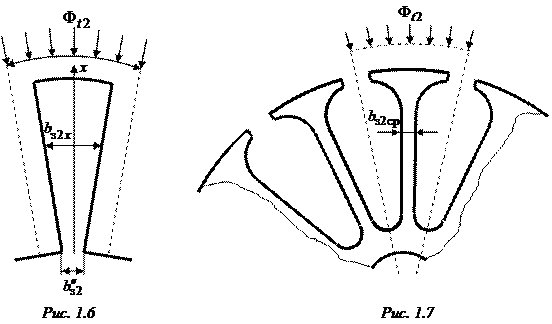
Рассмотрим каждый случай подробнее.

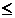 1,8 Тл. При этом условии зубцы якоря практическине насыщеныи весь магнитный поток
1,8 Тл. При этом условии зубцы якоря практическине насыщеныи весь магнитный поток 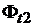 проходит только по зубцу, а магнитные потоки через прилегающиек зубцу пазы отсутствуют.
проходит только по зубцу, а магнитные потоки через прилегающиек зубцу пазы отсутствуют.
Построим зависимость распределения напряженности магнитного поля в зубце по высоте зубца 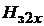 =
= 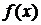 (рис. 1.8). Для этого предварительно рассчитаем зубцовый шаг и ширину зубца якоря для трех значений ординаты
(рис. 1.8). Для этого предварительно рассчитаем зубцовый шаг и ширину зубца якоря для трех значений ординаты 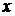 = =
= = 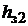 ;
; 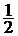
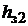 ;
; 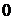 :
:
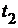 =
= 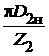 ;
; 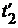 =
= 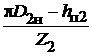 ;
; 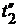 =
= 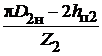 ; (1.21)
; (1.21)
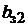 =
= 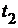 –
– 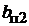 ;
; 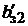 =
= 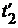 –
– 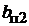 ;
; 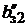 =
= 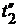 –
– 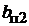 . (1.22)
. (1.22)
По выражению (1.19) с учетом (1.21) и (1.22) вычисляются значения магнитных индукций по вершине, по середине и в основании зубца:
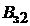 =
= 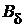
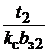 ;
; 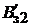 =
= 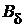
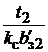 ;
; 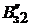 =
= 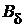
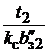 . (1.23)
. (1.23)
По кривым намагничивания электротехнической стали [1]–[3]для значений магнитныхиндукций, полученныхв (1.23), определяютсясоответствующиеим значения напряженностей магнитного поля для трех сечений зубца 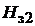 (по вершине при
(по вершине при 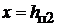 ),
), 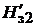 (по середине высоты зубца при
(по середине высоты зубца при 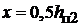 ) и
) и 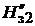 (в основании зубца при
(в основании зубца при 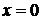 ).
).
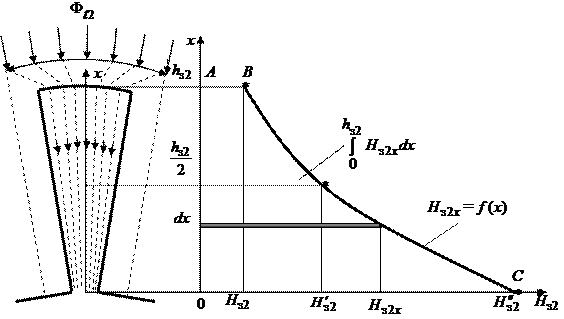
Рис. 1.8
По мере приближения к основанию зубца ширина зубца уменьшается, обуславливая возрастание магнитной индукции. Как следует из рис. 1.8,приближение к основанию зубца сопровождается быстрым нарастанием напряженность магнитного поля 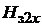 .
.
На основании закона полного тока с учетом того, что силовая линия полезного магнитного потока проходит через зубцовую зону дважды, МДС зубцов определяется выражением
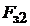 = 2
= 2 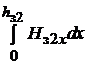 . (1.24)
. (1.24)
Формально интеграл в правой части выражения (1.24) численно равен площади фигуры 0АВС0. Но так как аналитическое выражение для зависимости 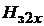 =
= 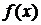 отсутствует, тодля вычисления этого интеграла воспользуемсяформулойпарабол(формула Симпсона),всоответствиискоторой
отсутствует, тодля вычисления этого интеграла воспользуемсяформулойпарабол(формула Симпсона),всоответствиискоторой
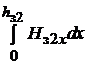 =
= 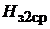
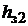 , (1.25)
, (1.25)
где 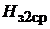 – среднее расчетное значение напряженности магнитного поля в зубце якоря, определяемое выражением
– среднее расчетное значение напряженности магнитного поля в зубце якоря, определяемое выражением
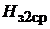 =
= 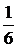 (
( 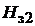 +
+ 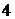
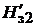 +
+ 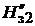 ). (1.26)
). (1.26)
 Таким образом, МДС зубцовой зоны якоря при ненасыщенной зубцовой зоне определяется выражением
Таким образом, МДС зубцовой зоны якоря при ненасыщенной зубцовой зоне определяется выражением
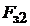 =
= 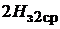
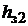 .(1.27)
.(1.27)
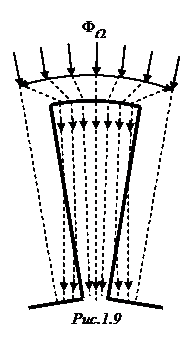
 > 1,8 Тл.При таком значении магнитной индукции зубец насыщается, магнитная проницаемость стали снижается и магнитный поток вытесняется из зубца в прилегающие пазы (рис. 1.9).
> 1,8 Тл.При таком значении магнитной индукции зубец насыщается, магнитная проницаемость стали снижается и магнитный поток вытесняется из зубца в прилегающие пазы (рис. 1.9).
В результате, в отличие от предыдущего случая,магнитный поток в зубце по его высоте по мере приближения к основанию уменьшается. Поэтому для произвольного сечения зубца на высоте 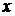 от его основания имеем
от его основания имеем
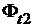 =
= 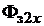 +
+ 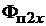 ,(1.28)
,(1.28)
где 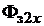 и
и 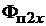 – магнитные потоки через зубец и через прилегающие к нему пазы на одной высоте
– магнитные потоки через зубец и через прилегающие к нему пазы на одной высоте 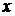 относительно основания зубца.
относительно основания зубца.
Разделим левую и правую части выражения(1.28) на площадь сечения зубца 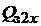 на высоте
на высоте 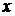 и тогда получим
и тогда получим
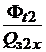 =
= 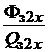 +
+ 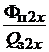 . (1.29)
. (1.29)
Дробь в левой части выражения (1.29) определяет расчетную магнитную индукцию в зубце 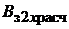 в предположении, что весь магнитный поток
в предположении, что весь магнитный поток 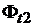 проходит через зубец, т.е. насыщение зубца не учитывается, тогда
проходит через зубец, т.е. насыщение зубца не учитывается, тогда
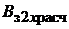 =
= 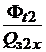 . (1.30)
. (1.30)
Первое слагаемое в правой части определяет действительную магнитную индукцию в зубце на высоте 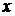 от основания зубца:
от основания зубца:
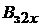 =
= 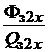 . (1.31)
. (1.31)
Второе слагаемое в правой части выражения (1.29) в представленном виде непосредственно физического смысла не имеет.
Преобразуем это второе слагаемое в правой части(1.29), умножив и раз-
делив его на площадь сечения паза 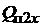 на высоте
на высоте 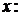
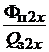 =
= 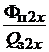
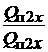 =
= 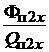
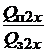 . (1.32)
. (1.32)
Первый сомножитель в правой части выражения (1.32) определяет действительную магнитную индукцию в пазу 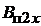 на высоте
на высоте 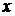 от основания паза:
от основания паза:
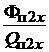 =
= 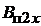 . (1.33)
. (1.33)
Второй сомножитель в правой части выражения (1.32)после дополнительных преобразований примет вид
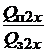 =
= 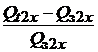 =
= 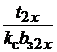 – 1=
– 1= 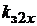 , (1.34)
, (1.34)
где 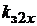 – зубцовый коэффициент, зависящий от геометрии зубцовой зоны и однозначно определяемый размерами этой зубцовой зоны на высоте
– зубцовый коэффициент, зависящий от геометрии зубцовой зоны и однозначно определяемый размерами этой зубцовой зоны на высоте 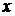 .
.
Принимая во внимание обозначения (1.33) и (1.34), запишем правую часть (1.32) в следующем виде:
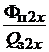 =
= 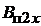
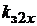 . (1.35)
. (1.35)
Подставляя выражения (1.31) и (1.35) в (1.29), получим
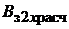 =
= 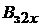 +
+ 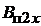
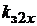 . (1.36)
. (1.36)
Магнитную индукцию в пазу 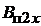 можно выразить через напряженность магнитного поля в пазу
можно выразить через напряженность магнитного поля в пазу 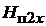 и магнитную проницаемость воздуха
и магнитную проницаемость воздуха  :
:
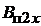 =
= 
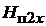 . (1.37)
. (1.37)
Здесьи в дальнейшем предполагается, что магнитная проницаемость воздуха равна магнитной проницаемости вакуума.
Подставляя (1.37) в (1.36), получим
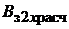 =
= 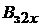 +
+ 
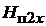
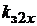 . (1.38)
. (1.38)
В пределахзубцовогоделениямагнитныйпоток идет параллельнымипутями через зубеци прилегающие к нему пазы, следовательно, падение магнитного потенциала в зубцах и в пазах должно быть одинаковым на одной высоте 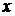 , а значит, одинаковыми должны быть напряженности магнитного поля в зубце
, а значит, одинаковыми должны быть напряженности магнитного поля в зубце 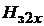 и в прилегающих к этому зубцу соседних пазах
и в прилегающих к этому зубцу соседних пазах 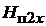 на одной высоте от основания зубца, т.е.
на одной высоте от основания зубца, т.е. 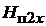 =
= 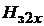 .С учетом этого условия выражение (1.38) примет вид
.С учетом этого условия выражение (1.38) примет вид
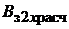 =
= 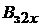 +
+ 
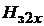
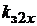 . (1.39)
. (1.39)
В выражении (1.39) напряженность магнитного поля 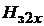 соответствует магнитной индукции
соответствует магнитной индукции 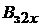 (рис. 1.9). На рис. 1.10 представлена графическая интерпретация выражения (1.39).
(рис. 1.9). На рис. 1.10 представлена графическая интерпретация выражения (1.39).
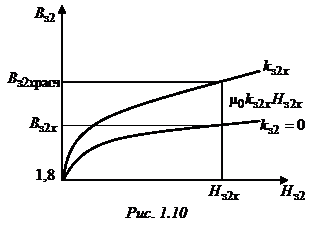 Кривая с
Кривая с 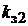 = 0 определяет основную кривую намагничивания материала, а вторая кривая, соответствующаянекоторому значению зубцового коэффициента
= 0 определяет основную кривую намагничивания материала, а вторая кривая, соответствующаянекоторому значению зубцового коэффициента 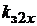 , строится по выражению (1.39) для ряда значений магнитной индукции
, строится по выражению (1.39) для ряда значений магнитной индукции 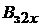 . Так, например, для магнитной индукции
. Так, например, для магнитной индукции 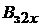 по основной кривой намагничивания определяется напряженность магнитного поля
по основной кривой намагничивания определяется напряженность магнитного поля 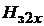 , затем вычисляется произведение
, затем вычисляется произведение 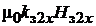 и рассчитывается магнитная индукция
и рассчитывается магнитная индукция 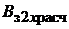 . Отсчет магнитных индукций по оси ординат начинается с 1,8 Тл, так как при
. Отсчет магнитных индукций по оси ординат начинается с 1,8 Тл, так как при 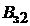 < 1,8 Тл (зубцы не насыщены и весь магнитный поток, соответствующий зубцовому делению, проходит через зубец) все кривые сливаются в основную кривую намагничивания. По этому принципу строится семейство кривых
< 1,8 Тл (зубцы не насыщены и весь магнитный поток, соответствующий зубцовому делению, проходит через зубец) все кривые сливаются в основную кривую намагничивания. По этому принципу строится семейство кривых 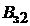 = f(
= f( 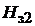 ) для нескольких значений коэффициента
) для нескольких значений коэффициента 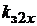 [1]–[3].Полученное таким путем семейство кривых
[1]–[3].Полученное таким путем семейство кривых 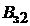 =f(
=f( 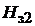 ) в [1]–[3]дает возможность определить напряженность магнитного поля в тех сечениях зубца, в которых
) в [1]–[3]дает возможность определить напряженность магнитного поля в тех сечениях зубца, в которых 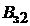 > 1,8Тл. Для остальных сечений зубца напряженность магнитного поля
> 1,8Тл. Для остальных сечений зубца напряженность магнитного поля 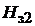 определяетсякак и при
определяетсякак и при 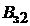 < 1,8 Тл.
< 1,8 Тл.
В остальном расчет МДС зубцовой зоныякоря приусловии 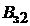 > 1,8Тлвыполнятся так же, как и при
> 1,8Тлвыполнятся так же, как и при 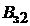 < 1,8 Тл.
< 1,8 Тл.
1.7. Кривая намагничивания магнитной системы
машины постоянного тока
Магнитная система машины постоянного тока включает в себя пять участков,поэтомуМДСмагнитнойсистемы,или,соответственно, МДС обмотки возбуждения машины, будет содержать пять составляющих:
 =
= 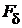 +
+ 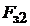 +
+ 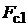 +
+ 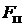 +
+ 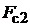 . (1.40)
. (1.40)
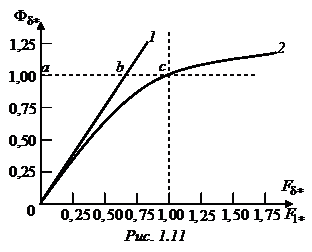 Расчет составляющих МДСи самой МДС выполняется для нескольких значений полезного магнитного потока
Расчет составляющих МДСи самой МДС выполняется для нескольких значений полезного магнитного потока 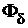 , и по результатам этого расчета строится кривая намагничивания магнитной системы
, и по результатам этого расчета строится кривая намагничивания магнитной системы 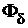 = f(
= f(  ) (рис. 1.11). Для удобства указанная зависимость строится в относительных единицах, в которых за базовые значения принимаются номинальные значения полезного магнитного потока
) (рис. 1.11). Для удобства указанная зависимость строится в относительных единицах, в которых за базовые значения принимаются номинальные значения полезного магнитного потока 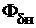 и МДС обмотки возбуждения
и МДС обмотки возбуждения 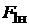 , так что
, так что 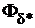 =
= 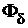 /
/ 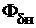 ,
, 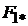 =
=  /
/ 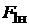 и
и 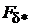 =
= 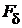 /
/ 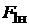 .
.
На рис. 1.11 представлены зависимости полезного магнитного потока 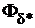 в функции МДС
в функции МДС 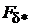 воздушного зазора
воздушного зазора 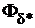 = f(
= f( 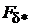 ) (кривая 1) и полезного магнитного потока
) (кривая 1) и полезного магнитного потока 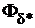 в функции МДС
в функции МДС 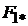 возбуждения
возбуждения 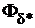 = f(
= f( 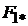 ) (кривая 2). В своей начальной части кривая намагничивания 2 практически линейна, так как при малых значениях магнитного потока магнитное сопротивление стали мало и
) (кривая 2). В своей начальной части кривая намагничивания 2 практически линейна, так как при малых значениях магнитного потока магнитное сопротивление стали мало и 
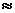
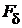 . По мере увеличения полезного магнитного потока
. По мере увеличения полезного магнитного потока 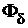 магнитное сопротивление ферромагнитных участков и – особенно –зубцового слоя возрастает, вследствие чего зависимость
магнитное сопротивление ферромагнитных участков и – особенно –зубцового слоя возрастает, вследствие чего зависимость 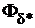 =f(
=f( 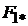 )отклоняется от линейной.
)отклоняется от линейной.
Проведем через точку 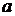 , соответствующую
, соответствующую 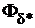 =1,00, горизонтальную прямую, пересекающуюхарактеристики 1 и 2. Обозначим через
=1,00, горизонтальную прямую, пересекающуюхарактеристики 1 и 2. Обозначим через 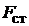 падениемагнитного потенциала на стальных участках магнитной цепи:
падениемагнитного потенциала на стальных участках магнитной цепи:
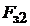 +
+ 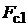 +
+ 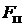 +
+ 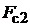 =
= 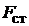 .
.
С учетом этого обозначениявыражение(1.40) примет вид
 =
= 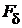 +
+ 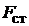 .
.
Отрезок 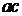 на рис. 1.11определяет МДС возбуждения, отрезок
на рис. 1.11определяет МДС возбуждения, отрезок 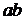 – МДС воздушного зазора, а отрезок
– МДС воздушного зазора, а отрезок 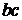 – МДС стальных участков магнитной цепи
– МДС стальных участков магнитной цепи 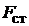 .
.
Степень насыщения магнитной цепи характеризуется коэффициентом насыщения:
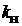 =
= 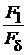 =
= 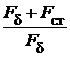 = 1+
= 1+ 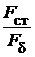 =
= 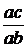 =
= 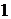 +
+ 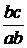 . (1.41)
. (1.41)
Малые значения коэффициента насыщения характеризуют плохое использование стали магнитной системы, и машина имеет значительные габариты и массу. При больших значениях коэффициента насыщения возрастает МДС обмотки возбуждения, вызывая увеличение числа ее витков и сечение провода, а следовательно, повышенный расход меди. Таким образом, ненасыщенная машина или, наоборот, машина с очень большим насыщением характеризуется большим расходом активных материалов: меди обмотки возбуждения и стали магнитной системы. В общепромышленных машинах коэффициент насыщения магнитной системы, определяемый выражением (1.41), равен 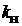 = 1,25…1,45. При таких значениях
= 1,25…1,45. При таких значениях 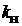 суммарная масса меди обмотки возбуждения истали магнитной цепи машины оказывается минимальной.
суммарная масса меди обмотки возбуждения истали магнитной цепи машины оказывается минимальной.
При постоянной скорости вращения ЭДС обмотки якоря 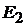 пропорциональна полезному магнитному потоку
пропорциональна полезному магнитному потоку 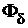 пары полюсов,а МДС обмотки возбуждения
пары полюсов,а МДС обмотки возбуждения  при фиксированном числе витков этой обмотки пропорциональна току возбуждения
при фиксированном числе витков этой обмотки пропорциональна току возбуждения  . Из этого следует, что в другом масштабе кривая намагничивания магнитной системы машины
. Из этого следует, что в другом масштабе кривая намагничивания магнитной системы машины 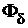 = f(
= f(  ) представляет собой характеристику холостого хода этой машины
) представляет собой характеристику холостого хода этой машины 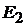 =
= 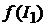 . Форма кривой такой характеристики существенно влияет на рабочие свойства машины постоянного тока (например, изменение напряжения на зажимах обмотки якоря при нагрузке, регулирование скорости вращения в двигателях). Рабочая точка с, соответствующая номинальному режиму, располагается, как правило, на колене кривой намагничивания магнитной системы машины
. Форма кривой такой характеристики существенно влияет на рабочие свойства машины постоянного тока (например, изменение напряжения на зажимах обмотки якоря при нагрузке, регулирование скорости вращения в двигателях). Рабочая точка с, соответствующая номинальному режиму, располагается, как правило, на колене кривой намагничивания магнитной системы машины  = f(
= f(  ).
).
