Порядок расчета МДС участков магнитной цепи
ОБЩИЕ ВОПРОСЫ ТЕОРИИ ЭЛЕКТРИЧЕСКИХ МАШИН ПОСТОЯННОГО ТОКА
Учебное пособие
Санкт-Петербург
Издательство СПбГЭТУ «ЛЭТИ»
УДК 621.313
ББК3 261я7
В12
Ваганов М. А.
В12Общие вопросы теории электрических машин постоянного тока: Учеб. пособие. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2012. 72 с.
ISBN978-5-7629-1206-8
Рассмотрены конструктивная схема магнитной системы машины постоянного тока и особенности расчета магнитодвижущихсил отдельных участков магнитной системы. Изложены принципы составления схем якорных обмотокс соответствующими примерами и выполнен анализ свойств разных типов якорных обмоток. Анализируются реакция якоря машины постоянного тока, т.е. действие собственного магнитного поля обмотки якоря на магнитное поле обмотки возбуждения, и коммутационные процессы в якорных обмотках
Предназначено для студентов, обучающихся по направлению «Электроэнергетика и электротехника» по профилю подготовки бакалавров «Электромеханика».
УДК 621.313
ББК3 261я7
Рецензенты: кафедра теории электротехники, электрических машин и аппаратовВоенно-морскогоинженерногоинститута;ведущийинженер Д.Г.РудаковОАО «Силовые машины».
Утверждено
редакционно-издательским советом университета
в качестве учебного пособия
 ISBN978-5-7629-1206-8 © СПбГЭТУ «ЛЭТИ», 2012
ISBN978-5-7629-1206-8 © СПбГЭТУ «ЛЭТИ», 2012
1. МАГНИТНАЯ СИСТЕМА МАШИНЫ ПОСТОЯННОГО ТОКА
И ЕЕ РАСЧЕТ
1.1. Конструктивная схема магнитной системы
машины постоянного тока
Магнитная система вместе с источником магнитного потока образует магнитную цепь машины, которая служит для создания и проведения магнитного потока. В этой магнитной цепи магнитная система играет роль магнитопровода. Задача расчета магнитной системы заключается в определении магнитодвижущей силы (МДС), необходимой для создания в магнитной цепи магнитного потока заданного значения.
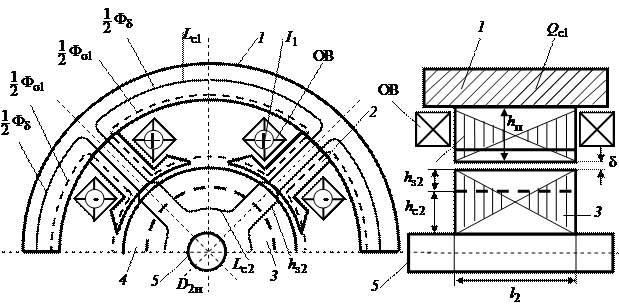
Рис.1.1
Конструктивная схема магнитной цепи машины постоянного тока представлена на рис. 1.1. Магнитная система машины постоянного тока состоит из вращающейся и неподвижной частей. К неподвижной части относятся станина 1 и главные полюса 2. Пакет стали якоря 3 образует подвижную или вращающуюся часть магнитной системы. Все элементы магнитной системы выполнены из магнитомягких материалов с достаточно высокой магнитной проницаемостью. Станина является одновременно конструктивным элементом машины, так как к ней крепятся главные и добавочные полюсы и на ее базе, по существу, производится сборка всей машины.
Станина в большинстве случаев является массивной и выполняется методом литья из стали 10. Главные полюсы и якорь изготавливаются из листовой электротехнической стали и являются шихтованными. Пакет стали якоря напрессовывается на вал 5 и вращается вместе с ним. По наружной цилиндрической поверхности пакета стали якоря размещаются пазы, в которых располагается обмотка якоря. Вращающаяся и неподвижные части магнитной системы разделены воздушным зазором 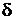 , который составляет доли миллиметровв машинах малой мощности и достигает нескольких миллиметровв крупных машинах постоянного тока.
, который составляет доли миллиметровв машинах малой мощности и достигает нескольких миллиметровв крупных машинах постоянного тока.
На сердечниках главных полюсов 2 располагаются катушки обмотки возбуждения (ОВ). По ОВ проходит постоянный ток возбуждения  , который создает магнитный поток ОВ
, который создает магнитный поток ОВ 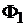 . Этот магнитный поток имеет две составляющие: главный, или полезный, магнитный поток
. Этот магнитный поток имеет две составляющие: главный, или полезный, магнитный поток 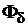 и магнитный поток рассеяния
и магнитный поток рассеяния 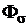 , т.е.
, т.е.
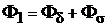 . (1.1)
. (1.1)
Силовые линии полезного магнитного потока  дважды пересекают воздушный зазор
дважды пересекают воздушный зазор  и замыкаются через пакет стали якоря 3. Магнитный поток
и замыкаются через пакет стали якоря 3. Магнитный поток 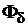 участвует в преобразовании энергии.Силовые линии магнитного потокарассеяния
участвует в преобразовании энергии.Силовые линии магнитного потокарассеяния 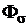 замыкаются через междуполюсное пространство, минуя якорь и, соответственно, обмотку якоря, и поток
замыкаются через междуполюсное пространство, минуя якорь и, соответственно, обмотку якоря, и поток 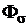 в преобразовании энергии не участвует.
в преобразовании энергии не участвует.
Запишем выражение (1.1) в виде
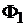 =
= 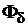
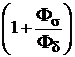 =
= 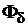
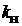 ; (1.2)
; (1.2)
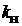 =
= 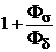 ,
,
где 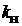 = 1,12…1,45 – коэффициент насыщения магнитной системы,который характеризует качество магнитной системы. Если значения коэффициента
= 1,12…1,45 – коэффициент насыщения магнитной системы,который характеризует качество магнитной системы. Если значения коэффициента 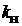 находятся в указанных пределах, то это соответствует минимуму суммарной массы стали магнитной системы и меди обмотки возбуждения.
находятся в указанных пределах, то это соответствует минимуму суммарной массы стали магнитной системы и меди обмотки возбуждения.
В соответствии с рис. 1.1 силовые линии полезного магнитного потока 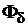 проходят по пяти участкам магнитной системы: станина, главные полюсы (дважды), воздушный зазор
проходят по пяти участкам магнитной системы: станина, главные полюсы (дважды), воздушный зазор 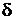 (дважды), зубцовая зона якоря 4 (дважды) и сердечник якоря 3.
(дважды), зубцовая зона якоря 4 (дважды) и сердечник якоря 3.
Введем следующие обозначения, характеризующиеперечисленныеучастки магнитной системы: 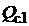 – площадь поперечного сечения станины относительно магнитного потока;
– площадь поперечного сечения станины относительно магнитного потока; 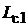 – длина пути средней магнитной силовой линии в станине;
– длина пути средней магнитной силовой линии в станине; 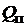 – площадь поперечного сечения главного полюса относительно магнитного потока; 2
– площадь поперечного сечения главного полюса относительно магнитного потока; 2 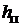 – длина пути средней магнитной силовой линии в главных полюсах (
– длина пути средней магнитной силовой линии в главных полюсах ( 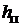 – высота одного главного полюса); 2
– высота одного главного полюса); 2 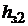 – длина пути средней магнитной силовой линии в зубцовой зоне якоря 4 (
– длина пути средней магнитной силовой линии в зубцовой зоне якоря 4 ( 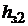 – высота зубца якоря);
– высота зубца якоря); 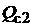 – площадь поперечного сечения сердечника якоря относительно магнитного потока;
– площадь поперечного сечения сердечника якоря относительно магнитного потока; 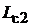 – длина пути средней магнитной силовой линии в сердечнике якоря.
– длина пути средней магнитной силовой линии в сердечнике якоря.
Обозначим через 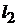 длину пакета стали якоря и через
длину пакета стали якоря и через 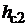 высоту сердечника якоря,и тогда площадь поперечного сечения сердечника якоря
высоту сердечника якоря,и тогда площадь поперечного сечения сердечника якоря 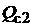 = =
= = 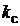
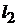
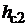 , где
, где 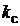 = 0,97 – коэффициент заполнения пакета якоря сталью (учитывает толщину изоляции листов стали и возможный зазор между соседними листами). Аналогично, обозначая через
= 0,97 – коэффициент заполнения пакета якоря сталью (учитывает толщину изоляции листов стали и возможный зазор между соседними листами). Аналогично, обозначая через 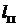 – осевую длину главного полюса
– осевую длину главного полюса
(в направлении оси машины) и через 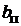 – ширину сердечника главного полюса, составим выражение, определяющее поперечное сечение сердечника полюса
– ширину сердечника главного полюса, составим выражение, определяющее поперечное сечение сердечника полюса 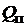 =
= 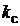
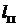
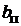 . В большинстве случаев длина пакета стали якоря
. В большинстве случаев длина пакета стали якоря 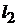 на несколько миллиметровбольше осевой длины главного полюса
на несколько миллиметровбольше осевой длины главного полюса 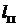 .
.
Расчет падения магнитного потенциала на отдельных участках магнитной системы и определение МДС магнитной системы в целом выполняются на основании закона полного тока.
Закон полного тока
Пусть имеем систему проводников с токами 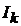 , которые пронизывают некоторую разомкнутую поверхность
, которые пронизывают некоторую разомкнутую поверхность 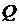 , ограниченную замкнутым контуром
, ограниченную замкнутым контуром 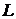 (рис. 1.2). Применительно к этому случаю закон полного тока может быть записан в следующем виде:
(рис. 1.2). Применительно к этому случаю закон полного тока может быть записан в следующем виде:
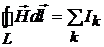 . (1.3)
. (1.3)
Данное выражение представляет собой математическую формулировку закона полного тока: циркуляция вектора напряженности магнитного поля 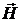 по любому замкнутому контуру
по любому замкнутому контуру 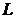 равнаалгебраическойсумме токов впроводниках
равнаалгебраическойсумме токов впроводниках 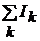 ,пронизывающихповерхность
,пронизывающихповерхность 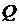 ,ограниченнуюданнымконтуром
,ограниченнуюданнымконтуром 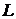 .
.
Из формулировки закона полного тока имеем два следствия:
– значение контурного интеграла в выражении закона полного тока не зависит от формы контура, так как оно определяется только суммой токов через поверхность, ограниченную контуром;
– если при изменении формы контура какой-либо из проводников с током оказывается за пределами контура или, наоборот, в пределах контура оказывается еще один проводник с током, то значение контурного интеграла изменяется скачком на силу тока в этом проводнике с учетом его направления.

Рис. 1.2
В электромеханике вводится обозначение
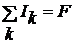 . (1.4)
. (1.4)
В выражении (1.4)величина F представляет собой магнитодвижущую силу (МДС), которая измеряется в амперах и численно равна току, создающему в некоторой точке пространства магнитное поле напряженности Н.
Для определения МДС F необходимо вычислить контурный интеграл в левой части выражения (1.3).
Раскрывая скалярное произведение в контурном интеграле в выражении (1.3), получим
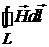 =
= 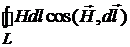 .
.
В последующих преобразованиях воспользуемся первым следствием из закона полного тока о независимости значения интеграла от формы контура 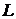 и выберем такой контур интегрирования, в каждой точке которого угол между векторами
и выберем такой контур интегрирования, в каждой точке которого угол между векторами 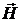 и
и 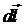 будет равен нулю. Такому требованию в простейшем случае удовлетворяет любая силовая линия магнитного поля ипо определению называется некоторая замкнутая кривая, касательная к которой в каждой точке совпадает по направлению с вектором напряженности магнитного поля в этой точке.
будет равен нулю. Такому требованию в простейшем случае удовлетворяет любая силовая линия магнитного поля ипо определению называется некоторая замкнутая кривая, касательная к которой в каждой точке совпадает по направлению с вектором напряженности магнитного поля в этой точке.
Выберем в качестве контура интегрирования L одну из силовых линий 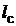 рассматриваемого магнитного поля при условии, что эта силовая линия охватывает данную систему проводников с токами. Для силовой линии магнитного поля скалярное произведение векторов
рассматриваемого магнитного поля при условии, что эта силовая линия охватывает данную систему проводников с токами. Для силовой линии магнитного поля скалярное произведение векторов 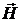 и
и 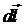 равно их обычному произведению, так как угол между этими векторами равен нулю. С учетом этого получим
равно их обычному произведению, так как угол между этими векторами равен нулю. С учетом этого получим
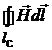 =
= 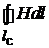 . (1.5)
. (1.5)
При вычислении контурного интеграла контур интегрирования всегда можно разбить на ряд участков, представив контурный интеграл в виде суммы криволинейных интегралов:
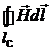 =
= 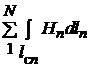 , (1.6)
, (1.6)
где N – число участков, на которые разбит контур интегрирования 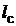 ; n – номер участка;
; n – номер участка; 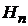 – напряженность магнитного поля в пределах n-го участка;
– напряженность магнитного поля в пределах n-го участка; 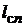 – длина n-го участка силовой линии.
– длина n-го участка силовой линии.
Каждый из криволинейных интегралов легко вычисляется, если подынтегральная функция (в данном случае это напряженность магнитного поля 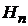 )
)
в пределах n-го участка является величиной постоянной; 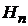 = const.Тогда
= const.Тогда
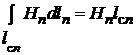 . (1.7)
. (1.7)
Подставляя (1.7)в (1.6), получим:
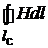
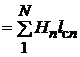 . (1.8)
. (1.8)
Произведение под знаком суммы 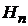
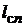 в выражении(1.8)представляет собой падение магнитного потенциала в пределахn-го участка или, что то же самое, МДС n-го участка
в выражении(1.8)представляет собой падение магнитного потенциала в пределахn-го участка или, что то же самое, МДС n-го участка 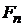 =
= 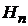
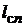 .
.
И тогда правая часть выражения (1.8)примет вид
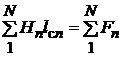 . (1.9)
. (1.9)
Возвращаясь к исходному контурному интегралу в выражении (1.5), окончательно получим
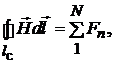 (1.10)
(1.10)
и, следовательно, значение контурного интеграла в выражении закона полного тока равно сумме МДСвсех участков, на которые был разбит контур интегрирования, т.е. силовая линия 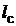 .
.
Требования к якорным обмоткам машин постоянного тока
Обмотка якоря машины постоянного тока является одним из трех функциональных элементов, так какнепосредственноучаствует в преобразовании механической энергии в электрическую энергиюв генераторах и электрической в механическую в двигателях. В соответствии с этим к якорным обмоткам предъявляются разнородные и часто противоречивые требования.
Обмотка якоря должна:
1) обеспечивать требуемые значения напряжения, тока и скорости вращения;
2) обладать достаточной механической прочностью, так как на неедействуют центробежные и электромагнитные силы.Изоляция обмотки должна выдерживать рабочее напряжение и при рабочей температуре не разрушаться и не терять свои изолирующие свойства. Таким образом, якорная обмотка обеспечивает необходимую механическую, термическую и электрическую прочностьмашины в течение эксплуатационного срока ееслужбы;
3) обеспечивать безыскровую работу щеточно-коллекторного узла;
4) обеспечивать достаточно высокие технико-экономические показатели машины (высокий КПД, малую массу и габариты, низкую стоимость);
5) быть достаточно простой в изготовлении и, обязательно, ремонтопригодной.
Петлевые обмотки
Для получения основных соотношений в простой петлевой обмотке составим предварительно фрагмент схемы этой обмотки безотносительно к конкретному числовому значению ее первогочастичного шага 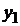 , например, при
, например, при 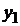 = 3 (рис. 2.4). На принципиальных схемах секции якорных обмоток изображаются, как правило, одновитковыми. Для наглядного изображения схем якорных обмоток цилиндрическую поверхность якоря вместе с обмоткой и коллектором развертывают на плоскость. Диаметр коллектора принимается равным диаметру якоря. Полученная таким путем схема обмотки называется развернутой.
= 3 (рис. 2.4). На принципиальных схемах секции якорных обмоток изображаются, как правило, одновитковыми. Для наглядного изображения схем якорных обмоток цилиндрическую поверхность якоря вместе с обмоткой и коллектором развертывают на плоскость. Диаметр коллектора принимается равным диаметру якоря. Полученная таким путем схема обмотки называется развернутой.
 В соответствии с числовым значением первого частичного шага
В соответствии с числовым значением первого частичного шага 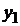 =3 активные стороны первой секции располагаются в пазах 1 и 4. Для удобства левые половины секцийобмотки изображаются на схемах сплошными линиями, а правые пунктирными. Выводы секции в простой петлевой обмотке присоединяются к двум соседним коллекторным пластинам (в данном случае к пластинам 1 и 2).
=3 активные стороны первой секции располагаются в пазах 1 и 4. Для удобства левые половины секцийобмотки изображаются на схемах сплошными линиями, а правые пунктирными. Выводы секции в простой петлевой обмотке присоединяются к двум соседним коллекторным пластинам (в данном случае к пластинам 1 и 2).
В простой петлевой обмотке последовательно соединенные секции всегда располагаются в соседних пазах. В данном случае конец первой секции соединяется через коллекторную пластину 2 с началом второй секции, начальная активная сторона которойнаходится в пазу 2. Секция 2 занимает пазы 2 и 5, а ее выводы присоединены к коллекторным пластинам2 и 3.
Взаимное расположение на схеме двух последовательно соединенных секцийобмоткиопределяетсявторым частичным шагом 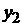 и результирующим шагом обмотки
и результирующим шагом обмотки 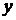 . Второй частичный шаг
. Второй частичный шаг 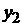 равен числу зубцов, расположенных между пазами, в которых расположены конечная активная сторона одной секции и начальная активная сторона секции,с ней последовательно соединенной (рис. 2.4;
равен числу зубцов, расположенных между пазами, в которых расположены конечная активная сторона одной секции и начальная активная сторона секции,с ней последовательно соединенной (рис. 2.4; 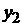 =2). Результирующий шаг обмотки
=2). Результирующий шаг обмотки 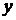 определяет расстояние в зубцах между пазами, в которых расположены начальные активные стороны двух последовательно соединенных секций (рис. 2.4;
определяет расстояние в зубцах между пазами, в которых расположены начальные активные стороны двух последовательно соединенных секций (рис. 2.4; 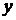 = 1).
= 1).
Кромешагов обмоткипо якорю вводится в рассмотрение шаг обмоткипо коллектору 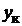 , измеряемый числом коллекторных делений, заключенныхмежду серединами коллекторных пластин, к которым присоединены начальнаяи конечная стороны одной секции. Для фрагмента схемы, представленной на рис. 2.4,
, измеряемый числом коллекторных делений, заключенныхмежду серединами коллекторных пластин, к которым присоединены начальнаяи конечная стороны одной секции. Для фрагмента схемы, представленной на рис. 2.4, 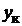 =1.
=1.
Определения для всех шагов обмотки по якорю 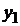 ,
, 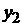 и
и 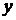 , а также для шага по коллектору
, а также для шага по коллектору 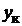 справедливы для всех типов якорных обмоток.
справедливы для всех типов якорных обмоток.
В соответствии с рис. 2.4 можно составить соотношение между шагами по якорю для простой петлевой обмотки:
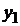 =
= 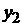 +
+ 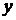 . (2.3)
. (2.3)
Также для простой петлевой обмотки всегда
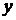 = 1. (2.4)
= 1. (2.4)
Это значит, что в простой петлевой обмотке последовательно соединенные секции всегда расположены в соседних пазах. В общем случае 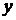 =
= 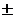 1. При знаке (+) обмотка правая, а при знаке (–) – левая, когда следующая секция располагается слева от исходной секции. На практике преимущественно используются правые обмотки.
1. При знаке (+) обмотка правая, а при знаке (–) – левая, когда следующая секция располагается слева от исходной секции. На практике преимущественно используются правые обмотки.
Для любой якорной обмотки машины постоянного тока справедливо соотношение
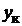 =
= 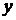 , (2.5)
, (2.5)
т. е. при составлении схемы обмотки при переходе от одной секции к другой сдвиг по якорю должен равняться сдвигу по коллектору. Применительно к простой петлевой обмотке,выводы или концы любой секции всегда присоединяются к двум соседним коллекторным пластинам.
В качестве примера составим развернутую схему простой петлевой обмотки со следующими данными: число секций обмотки якоря 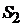 =15, число коллекторных пластин
=15, число коллекторных пластин 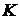 всегда равно числу секций и поэтому
всегда равно числу секций и поэтому 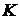 =15 и число зубцов (пазов) якоря
=15 и число зубцов (пазов) якоря 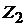 =15, т.е. в каждом пазу размещаются только две активные стороны двух различных секций. Число полюсов машины
=15, т.е. в каждом пазу размещаются только две активные стороны двух различных секций. Число полюсов машины 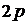 =4.
=4.
При составлении схемы любой обмотки якоря необходимо выполнить в учебных целях следующие действия:
1) рассчитать все шаги обмотки;
2) составить развернутую схему обмотки;
3) расставить на схеме геометрические нейтрали и полюсы;
4)выбрать направление перемещения схемы обмотки и указать направление ЭДС в активных сторонах секций обмотки якоря;
5) составить электрическую схему соединений секций обмотки якоряс указанием направлений ЭДС в секциях;
6) расставить щетки на коллекторе на развернутой схеме;
7) составить вторую электрическую схему соединений секций обмотки, указав на ней параллельные ветви;
8) сформулировать основные свойства простой петлевой обмотки.
Рассчитаем шаги обмотки якоря. Первый частичный шаг 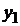 =
= 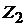 /2p
/2p 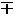
 ==
== 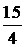
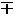
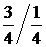 =3 или 4. Выбираем укороченный шаг
=3 или 4. Выбираем укороченный шаг 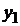 =3. Для простой петлевой обмотки результирующий шаг
=3. Для простой петлевой обмотки результирующий шаг 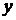 =1, и тогда второй частичный шаг в соответствии с выражением (2.3)
=1, и тогда второй частичный шаг в соответствии с выражением (2.3) 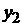 =
= 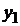 –
– 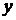 =3 – 1=2. Шаг обмотки по коллектору для любой якорной обмоткис учетом выражения (2.5)
=3 – 1=2. Шаг обмотки по коллектору для любой якорной обмоткис учетом выражения (2.5) 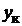 =1. По этим данным составляем развернутую схему обмотки, которая представлена на рис. 2.5.
=1. По этим данным составляем развернутую схему обмотки, которая представлена на рис. 2.5.

Рис.2.5
Составление схемы начинаем с паза 1, в котором размещаем начальную активную сторону секции 1, а ее конечная активная сторона располагается в соответствии с первым частичным шагом 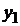 =3 в пазу 4. Выводы секции 1 присоединены к коллекторным пластинам 1 и 2 в соответствии с шагомобмотки по коллектору
=3 в пазу 4. Выводы секции 1 присоединены к коллекторным пластинам 1 и 2 в соответствии с шагомобмотки по коллектору 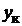 =1. С учетом шагов
=1. С учетом шагов 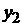 и
и 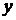 =1 размещаем секцию 2, занимающую пазы 2 и 5. Начало секции 2 через коллекторную пластину 2 соединено с концом секции 1. И в таком порядке составление схемы продолжается до последней секции 15. Конечная активная сторона этой секции через коллекторную пластину 1 соединяется с началом секции 1.Таким образом,после укладки всех 15 секций простая петлевая обмотка оказывается замкнутой, т.е. образует замкнутый электрический контур.
=1 размещаем секцию 2, занимающую пазы 2 и 5. Начало секции 2 через коллекторную пластину 2 соединено с концом секции 1. И в таком порядке составление схемы продолжается до последней секции 15. Конечная активная сторона этой секции через коллекторную пластину 1 соединяется с началом секции 1.Таким образом,после укладки всех 15 секций простая петлевая обмотка оказывается замкнутой, т.е. образует замкнутый электрический контур.
Полюсный шаг в зубцах 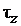 =
= 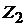 /2p=15/4=3
/2p=15/4=3 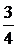 , и на развернутой схеме размещаем геометрические нейтрали ГН с интервалом
, и на развернутой схеме размещаем геометрические нейтрали ГН с интервалом 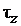 друг относительно друга. Затем наносим контуры полюсов в виде прямоугольников с интервалом
друг относительно друга. Затем наносим контуры полюсов в виде прямоугольников с интервалом 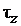 , полагая, что они размещаются над проводниками.
, полагая, что они размещаются над проводниками.
Предположим,что якорь вместе с обмоткой перемещается относитель-
но неподвижных полюсов слева направо с линейной скоростью 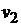 . Для удобства выберем такой момент времени взаимного расположения движущегося якоря и неподвижных полюсов, когда один из полюсов, например, северный N, размещается симметрично относительно секции 2, т.е. оси секции 2 и полюса Nсовпадают. По правилу правой руки определяем направление ЭДС в активных сторонах секций и на схеме указываем это направление стрелками. В проводниках, расположенных под северными полюсами, ЭДС направлена вверх, а в проводниках под южными полюсами – вниз.
. Для удобства выберем такой момент времени взаимного расположения движущегося якоря и неподвижных полюсов, когда один из полюсов, например, северный N, размещается симметрично относительно секции 2, т.е. оси секции 2 и полюса Nсовпадают. По правилу правой руки определяем направление ЭДС в активных сторонах секций и на схеме указываем это направление стрелками. В проводниках, расположенных под северными полюсами, ЭДС направлена вверх, а в проводниках под южными полюсами – вниз.
На основании развернутой схемы составим электрическую схему этой обмотки, представленную на рис. 2.6. Эта схема составлена в полном соответствии с развернутой схемой, и секции на ней соединены последовательно в том же порядке. При этом предполагалось, что начало любой секции находится слева от нее, если делать обход по часовой стрелке. Электрическая схема, как и развернутая, образует замкнутый контур. Из электрической схемы видно, что простая петлевая обмотка состоит из нескольких участков, в пределах каждого из которых последовательно соединенные секции имеют одинаковое направление ЭДС, а результирующие ЭДС соседних участковнаходятся в противофазе.Каждый из этих участков состоит из секций,расположенных в данный момент времени под одним из полюсов. Так, например, секции 13, 14, 15 и 1 расположены под левым южным полюсом, а секции 2,3, 4 и 5– под соседним справа северным полюсом, что и обуславливает смену направления ЭДС в секциях 2–5 относительно секций 13–1.
В данном случае число участков обмотки с одинаковым направлением ЭДС равно 4, как и 2р = 4. Если увеличим число секций 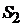 обмотки якоря при фиксированном числе полюсов, то возрастет число секций, приходящихся на один полюс, следовательно, увеличится длина каждого участка из секций с одинаковым направлением ЭДС, а число участков не изменится. Если же при фиксированном числе
обмотки якоря при фиксированном числе полюсов, то возрастет число секций, приходящихся на один полюс, следовательно, увеличится длина каждого участка из секций с одинаковым направлением ЭДС, а число участков не изменится. Если же при фиксированном числе 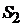 увеличить число полюсов, то уменьшится число секций обмотки под каждым полюсом, но возрастет число участков. Таким образом, в простой петлевой обмотке число участков обмотки, состоящих из секций с одинаковым направлением ЭДС,всегда равно числу полюсов.
увеличить число полюсов, то уменьшится число секций обмотки под каждым полюсом, но возрастет число участков. Таким образом, в простой петлевой обмотке число участков обмотки, состоящих из секций с одинаковым направлением ЭДС,всегда равно числу полюсов.
Рис. 2.6
Значение и направление ЭДС в секциях обмотки якоря определяется законом электромагнитной индукции и не зависит от положения щеток на коллекторе, а разность потенциаловмежду соседними разнополярными щетками существенно зависит от положения щеток на коллекторе. Эта разность потенциалов будет наибольшей, когда между соседними щетками будут находиться секции с одинаковым направлением ЭДС в них.
Исходя из этого, нетрудно сформулировать общее правило установки щеток на коллекторе. Щетки на коллекторе необходимо устанавливать на тех пластинах, относительно которых происходит смена направления ЭДС в секциях, присоединенных к этим пластинам. Из схемы на рис. 2.5 видно, что такие секции располагаются в зоне геометрических нейтралей слева и справа относительно каждой нейтрали,поэтому в общем случае каждую щетку необходимо размещать на коллекторе по линии геометрической нейтрали, которая на коллекторе смещена относительно геометрической нейтрали на якоре на половину полюсного деления при условии симметрии лобовых частей секций обмотки,поэтому,соответственно, щетки размещаются по осям главных полюсов. При данном условии между соседними щетками всегда будут находиться секции с одинаковым направлением ЭДС, а разность потенциалов между щетками будет максимально возможной. В простой петлевой обмотке ширина щетки 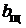 принимается равной ширине коллекторного деления
принимается равной ширине коллекторного деления 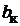 . Как видно из схемы на рис. 2.6,ЭДС соседних участков находятся в противофазе.
. Как видно из схемы на рис. 2.6,ЭДС соседних участков находятся в противофазе.
С другой стороны, если на рис. 2.6 все щетки одновременно сместить сгеометрических нейтралей в ту или другую сторону, то участки обмотки между щетками будут содержать секции с разным направлением ЭДС, а это приведет к уменьшению разности потенциалов между щетками.Чтобы снять ЭДС со всех участков обмотки, необходимо на коллекторе установить полный комплект щеток  , т.е. по числу пар полюсов, и тогда для простой петлевой обмотки
, т.е. по числу пар полюсов, и тогда для простой петлевой обмотки  =2р. Так как соседние участки обмотки расположены под разноименными полюсами, то результирующие ЭДС этих соседних участков находятся в противофазе.
=2р. Так как соседние участки обмотки расположены под разноименными полюсами, то результирующие ЭДС этих соседних участков находятся в противофазе.
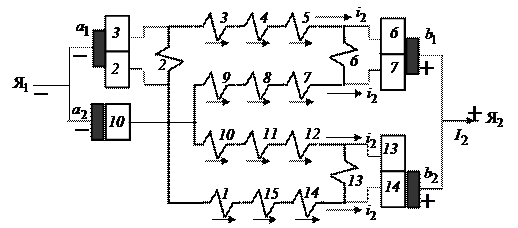
Рис.2.7
На основании электрической схемы рис. 2.6 можно составить еще одну электрическую схему (рис. 2.7). В данном случае три участка обмотки содержат по четыре секции, а один – только три (10, 11 и 12). Поэтому в замкнутом контуре простой петлевой обмотки в общем случае может действовать небольшая результирующая ЭДС, способная создать в этом контуре уравнительный ток. Как видно из электрической схемы на рис. 2.7, приустановке щеток строго на линиях геометрических нейтралей три секции обмотки якоря 2, 6 и 13 оказываются замкнутыми накоротко через щетки. В результате все участки обмотки будут содержать по три последовательно соединенные секции с одинаковым направлением ЭДС. Можно предположить, что теперь результирующие ЭДС этих участков будут одинаковыми, результирующая ЭДС в замкнутом контуре обмотки будет равна нулю и уравнительный ток в обмотке отсутствует.
При вращении обмотки с коллектором относительно неподвижных щеток (см. рис. 2.6) будет происходить изменение состава секций в участках междущетками и изменение направления ЭДС в секциях, переходящих из одного участка в другой, так что в целом разность потенциалов между соседними щетками будет оставаться постоянной.
На развернутой схеме обмотки щетки располагаются по осям полюсов, следовательно, расстояние между серединами соседних щеток равно полюсному шагу в зубцах  . Однополярные щетки
. Однополярные щетки 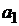 ,
, 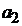 и
и 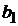 ,
, 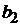 соединены между собой общими шинами. Условимся считать щетку положительной, если ток от нее идет во внешнюю цепь. Тогда щетки
соединены между собой общими шинами. Условимся считать щетку положительной, если ток от нее идет во внешнюю цепь. Тогда щетки 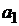 ,
, 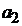 будут отрицательными, а щетки
будут отрицательными, а щетки 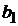 ,
, 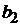 – положительными.
– положительными.
Если на электрической схеме простой петлевой обмотки (см. рис. 2.6) соединить между собой однополярные щетки, то получим вторую электрическую схему простой петлевой обмотки, представленную на рис. 2.7. На этой схеме относительно внешних зажимов обмотки якоря 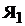 и
и 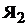 простая петлевая обмотка якоря образует четыре параллельные ветви. Параллельная ветвь– это участок обмотки, состоящий из последовательно соединенных секций с одинаковым направлением ЭДС (тока) в них. Если щетки размещены на геометрических нейтралях, то параллельные ветви будут состоять из секций с одинаковым направлением ЭДС.
простая петлевая обмотка якоря образует четыре параллельные ветви. Параллельная ветвь– это участок обмотки, состоящий из последовательно соединенных секций с одинаковым направлением ЭДС (тока) в них. Если щетки размещены на геометрических нейтралях, то параллельные ветви будут состоять из секций с одинаковым направлением ЭДС.
На рис. 2.7каждая из параллельных ветвей состоит из трех последовательно соединенных секций: 3, 4, 5; 7, 8, 9; 10, 11, 12 и 14, 15, 1, а секции 2, 6 и 13 замкнуты накоротко через соответствующие щетки. Электрическая схема, представленная на рис. 2.7, наглядно показывает распределение тока обмотки якоря и распределение секций этой обмотки по параллельным ветвям.
Числопараллельных ветвей обмотки якоряобозначается 2а, и для простой петлевой обмотки всегда 2а=2р, так как каждая из параллельных ветвейобразована секциями, расположенными под соответствующим полюсом. Обозначим через 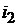 ток одной параллельной ветви обмотки якоря и через
ток одной параллельной ветви обмотки якоря и через 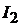 полный ток обмотки якоря. Тогда получим следующие соотношения между этими токами:
полный ток обмотки якоря. Тогда получим следующие соотношения между этими токами: 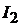 = 2а
= 2а 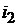 и
и 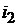 =
= 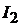 /2a.
/2a.
Каждая пара щеток обеспечивает работу соответствующей пары параллельных ветвей обмотки. Поэтому при неполном комплекте щеток ухудшается использование обмотки. В процессе эксплуатации возможны случаи нарушения щеточного контакта, т.е. отключение одной или нескольких щеток, что сопровождается снижением тока машины при работе ее генератором.
На основании изложенного можно сформулировать основные свойства простой петлевой обмотки:
· последовательно соединенные секции располагаются в соседних пазах,что определяется результирующим шагом обмотки 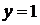 ;
;
· концыкаждой секции обмотки присоединяются к соседним коллекторным пластинам в соответствии с шагомпростойпетлевой обмотки по коллектору 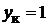 ;
;
· число параллельных ветвей обмотки якоря 2а=2р;
· число щеток на коллекторе 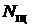 =2р.
=2р.
Для получения тока обмотки якоря более значительного, чем при простой петлевой обмотке и при ограниченном числе пар полюсов, необходимо увеличить число параллельных ветвей обмотки. С этой целью применяют сложные петлевые обмотки. Число параллельных ветвей в сложной петлевой обмотке 2а = 2рm, где m– число простых петлевых обмоток, из которых составлена сложная петлевая обмотка. Обычно m=2. Простые петлевые обмотки, образующие сложную петлевую обмотку, соединяются между собой параллельно с помощью щеток.
Шаги сложной петлевой обмотки по якорю и коллектору определяются выражениями
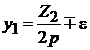 ; (2.6)
; (2.6)
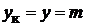 ; (2.7)
; (2.7)
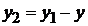 . (2.8)
. (2.8)
Извыражений(2.6) и (2.8)следует,чтопервыйи второйчастичныешагиобмотки определяютсяодними тем же выражением для простой и сложной петлевых обмоток.Выражение (2.7) показывает,что в сложной петлевой обмотке, во-первых, последовательно соединенные секции сдвинуты по якорю друг относительно друга на m зубцовых делений, т.е. расстояние между начальными активными сторонами двух последовательно соединенных секций составляет m зубцов, и, во-вторых, расстояниемежду серединами коллекторных пластин, к которым присоединенывыводы одной секции, равно m коллекторным делениям. Ширина щетки 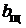 в сложной петлевой обмотке принимается равной m
в сложной петлевой обмотке принимается равной m 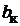 , т.е.
, т.е. 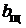 =m
=m 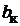 , где
, где 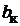 – ширина коллекторного деления.
– ширина коллекторного деления.
Волновые обмотки
Искрение на коллекторе
При работе машины постоянного тока в скользящем контакте между щетками и коллектором происходит, как правило, искрение. С практической точки зрения важно, чтобы работа скользящего контакта щетки происходила без значительного искрения у контактных поверхностей щеток, так как подобное искрение разрушает поверхность коллектора и щеток и ограничивает срок службы машины.
Причины, вызывающие искрение на коллекторе и под щетками, можно объединить в три группы: электромагнитного, потенциального и механического характера. Теоретические и экспериментальные исследования показывают, что в действительности процессы, происходящие в щеточных контактах, имеют достаточно сложную физико-химическую природу, и поэтому выделение и исследование какого-либо одного фактора оказывается практически невозможным.
К возможным причинам электромагнитного характера относятся: значительная плотность тока под щетками; напряжение размыкания между краем щетки и сбегающим краем коллекторной пластины, обусловленное запасом электромагнитной энергии секции; результирующая ЭДС, действующая в контуре коммутируемой секции; электрическая мощность, выделяющаяся в переходном сопротивлении щеточного контакта.
Большое влияние на искрение оказывает распределение потенциала по коллектору и, в частности, наибольшее возможное напряжение между соседними коллекторными пластинами 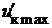 , которое наиболее резко проявляется в машинах без компенсационной обмотки. Это причины потенциального характера.
, которое наиболее резко проявляется в машинах без компенсационной обмотки. Это причины потенциального характера.
Механические причи
