Расчет силы тока через поперечное сечение проводника.
Расчет силы тока через поперечное сечение проводника.
Если ток протекает через площадь 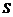 произвольной формы, то силу тока можно рассчитать по формуле
произвольной формы, то силу тока можно рассчитать по формуле
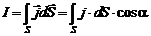 , (1.1)
, (1.1)
где вектор 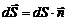 , а
, а 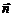 – это единичный вектор нормали к площадке
– это единичный вектор нормали к площадке 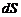 ; a – угол между векторами
; a – угол между векторами 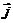 и
и 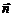 .
.
Если проводник сделан в виде тонкой полосы, и известна линейная плотность тока i, то полный ток можно найти по формуле:
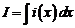 , (1.2)
, (1.2)
где dx – ширина полоски, вдоль которой течет ток dI
(см. рис. к задаче 3).
Задача 1
 По неоднородному цилиндрическому проводу радиуса R = 1 м течет ток. Найдите силу тока, протекающего через поперечное сечение проводника, если зависимость плотности тока от расстояния r до оси задается формулой
По неоднородному цилиндрическому проводу радиуса R = 1 м течет ток. Найдите силу тока, протекающего через поперечное сечение проводника, если зависимость плотности тока от расстояния r до оси задается формулой 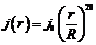 , где
, где 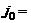 1 А/м2.
1 А/м2.
 Решение:
Решение:
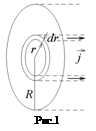
Разобъем поперечное сечение проводника (круг радиуса R) на кольца радиуса r и шириной dr (см. рис.1). Площадь такого кольца равна 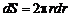 , а угол a между
, а угол a между 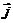 и
и 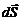 равен 0°. Используя формулу (1.1), найдем полный ток, протекающий через все поперечное сечение проводника:
равен 0°. Используя формулу (1.1), найдем полный ток, протекающий через все поперечное сечение проводника:
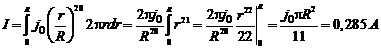
Ответ: I = 0,285 A
Задача 2
 По неоднородному проводу квадратного сечения
По неоднородному проводу квадратного сечения 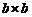 течет ток. Найдите силу тока, протекающего через поперечное сечение проводника, если плотность тока зависит от расстояния x от одной из боковых граней по закону
течет ток. Найдите силу тока, протекающего через поперечное сечение проводника, если плотность тока зависит от расстояния x от одной из боковых граней по закону 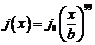 , где
, где 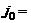 1 А/м2; b = 1 м.
1 А/м2; b = 1 м.
 Решение:
Решение:
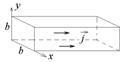
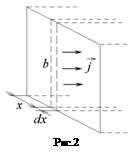
Разобъем поперечное сечение проводника (квадрат 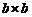 ) на узкие полоски шириной
) на узкие полоски шириной 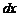 и высотой b (см. рис.2). Площадь такой полоски равна
и высотой b (см. рис.2). Площадь такой полоски равна 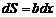 а угол a между
а угол a между 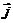 и
и 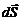 равен 0°. Используя формулу (1.1), найдем полный ток, протекающий через все поперечное сечение проводника:
равен 0°. Используя формулу (1.1), найдем полный ток, протекающий через все поперечное сечение проводника:
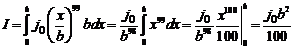
Ответ: I = 0,01 A
Задача 3
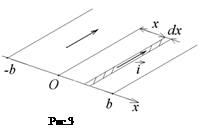 Вдоль средней линии проводящей полосы шириной 2b течет ток. Найдите силу тока, протекающего по всей полосе, если линейная плотность тока зависит от расстояния x до средней линии по закону
Вдоль средней линии проводящей полосы шириной 2b течет ток. Найдите силу тока, протекающего по всей полосе, если линейная плотность тока зависит от расстояния x до средней линии по закону 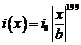 , где
, где 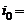 1 А/м; b = 1 м.
1 А/м; b = 1 м.
Решение:
Выделим на плоскости параллельно средней линии на расстоянии х узкую полоску шириной dx (см. рис.3). Используя формулу (1.2) найдем полный ток: 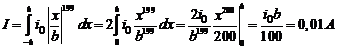
Ответ:I = 0,01 А
Суперпозиция магнитного поля,
Суперпозиция магнитного поля,
Созданного токами, протекающими в разных плоскостях.
Задача 5
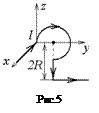 Ток
Ток 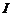 = 1 А течет по длинному проводу, изогнутому так, как показано на рис.5. Найдите индукцию магнитного поля, созданного этим током в центре окружности радиуса R = 1 м.
= 1 А течет по длинному проводу, изогнутому так, как показано на рис.5. Найдите индукцию магнитного поля, созданного этим током в центре окружности радиуса R = 1 м.
Решение:
Найдем отдельные вклады в индукцию магнитного поля в точке О (центр окружности), созданные двумя полубесконечными прямолинейными проводниками и проводником в виде дуги с углом разворота 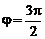 .
.
Для луча с током, текущим против оси х на расстоянии R от точки О, воспользуемся формулой (2.1):
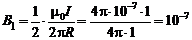 Тл
Тл
Для второго луча с током, текущим вдоль оси у на расстоянии 2R от точки О, также используем формулу (2.1):
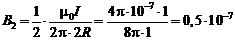 Тл
Тл
Для проводника в виде дуги в 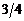 окружности радиусом R используем формулу (2.2):
окружности радиусом R используем формулу (2.2):
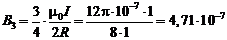 Тл
Тл
Направления векторов 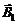 ,
, 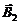 и
и 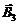 различны:
различны:
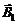 – направлен против оси z;
– направлен против оси z;
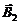 – направлен вдоль оси х;
– направлен вдоль оси х;
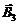 – направлен против оси х.
– направлен против оси х.
Используя принцип суперпозиции (2.4) и теорему Пифагора, найдем модуль индукции результирующего магнитного поля в точке О:
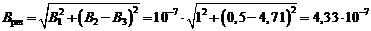 Тл
Тл
Ответ: 0,433 мкТл
Задача 6
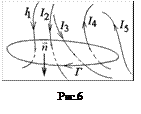 По длинным проводам различной конфигурации текут разные токи (см. рис.6). Найдите циркуляцию вектора индукции магнитного поля, созданного этими токами, по замкнутому контуру Г.
По длинным проводам различной конфигурации текут разные токи (см. рис.6). Найдите циркуляцию вектора индукции магнитного поля, созданного этими токами, по замкнутому контуру Г.
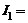 1 А,
1 А, 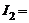 2 А,
2 А, 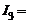 3 А,
3 А, 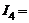 4 А,
4 А, 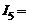 5 А.
5 А.
Решение:
Нарисуем вектор нормали 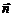 в соответствии с обходом Г по правилу правого винта (см. рис.6). Таким образом можно определить знак каждой силы тока, входящей в формулу (4.1) и найти циркуляцию:
в соответствии с обходом Г по правилу правого винта (см. рис.6). Таким образом можно определить знак каждой силы тока, входящей в формулу (4.1) и найти циркуляцию:
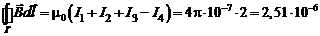 Тл×м
Тл×м
В этом примере учтено, что ток 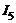 не пронизывает контур, поэтому и не входит в алгебраическую сумму в формуле (4.1)
не пронизывает контур, поэтому и не входит в алгебраическую сумму в формуле (4.1)
Ответ: 2,51 мкТл×м.
Задача 7
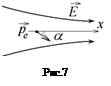 Электрический диполь с дипольным моментом
Электрический диполь с дипольным моментом 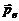 , удерживают в неоднородном электрическом поле на оси х под углом a к ней в точке с координатой
, удерживают в неоднородном электрическом поле на оси х под углом a к ней в точке с координатой 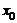 . Определите проекцию силы
. Определите проекцию силы 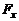 , действующей на диполь, если напряженность электрического поля на оси х меняется по закону
, действующей на диполь, если напряженность электрического поля на оси х меняется по закону 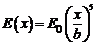 ,
,
где 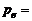 1 Кл×м;
1 Кл×м; 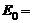 1 В/м; b = 1 м;
1 В/м; b = 1 м; 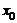 = 1 м; a = 60°.
= 1 м; a = 60°.
Решение:
По формуле (5.1) найдем зависимость энергии взаимодействия диполя и электрического поля:
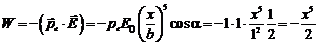
Из формулы (5.2) найдем проекцию силы на ось х в точке 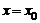 :
:
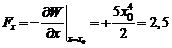 Н
Н
Ответ: 2,5 Н
 6. Э.Д.С. индукции и самоиндукции
6. Э.Д.С. индукции и самоиндукции
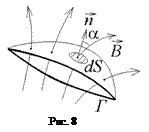 Рассмотрим замкнутый контур Г произвольной формы в неоднородном магнитном поле, который ограничивает некоторую поверхность S (см. рис.8). Потоком индукции магнитного поля сквозь эту поверхность называется величина
Рассмотрим замкнутый контур Г произвольной формы в неоднородном магнитном поле, который ограничивает некоторую поверхность S (см. рис.8). Потоком индукции магнитного поля сквозь эту поверхность называется величина
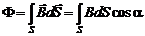 , (6.1)
, (6.1)
где a – угол между вектором 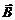 и нормалью
и нормалью 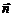 к площадке поверхности dS, которую магнитное поле пронизывает.
к площадке поверхности dS, которую магнитное поле пронизывает.
При изменении потока Ф во времени в контуре Г возникает Э.Д.С. индукции – электродвижущая сила, равная скорости изменения магнитного потока (закон электромагнитной индукции Фарадея):
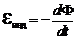 (6.2)
(6.2)
Если бы контур был сделан из проводящего вещества, то по нему потек бы электрический ток.
Поток Ф может изменяться по следующим причинам.
1) Изменяется индукция магнитного поля 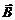 .
.
2) Изменяются геометрические размеры контура, т.е. изменяется площадь S.
3) Изменяется ориентация контура в пространстве, т.е. изменяется угол a.
В случае 1) в пространстве возникает вихревое электрическое поле 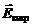 , действующее на свободные электроны проводящего контура.
, действующее на свободные электроны проводящего контура.
В случаях 2) и 3) из-за перемещения проводника в магнитном поле на свободные электроны в нем действует сила Лоренца.
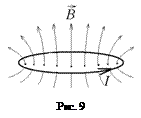 Если рассмотреть контур, по которому протекает ток I (см. рис.9), то индукция
Если рассмотреть контур, по которому протекает ток I (см. рис.9), то индукция 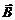 порождаемого этим током магнитного поля создает сквозь поверхность контура поток, пропорциональный силе тока I:
порождаемого этим током магнитного поля создает сквозь поверхность контура поток, пропорциональный силе тока I:
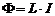 , (6.3)
, (6.3)
где коэффициент пропорциональности L называется индуктивностью контура. Если ток в контуре начинает изменяться, то в нем возникнет Э.Д.С. самоиндукции:
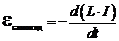 (6.4)
(6.4)
Знак "–" в формулах (6.2) и (6.4) означает, что при изменении магнитного потока сквозь замкнутый контур в нем возникает такая Э.Д.С., которая стремится уменьшить изменение потока.Это правило Ленца.В результате увеличения силы тока на рис. 9, а следовательно и индукции 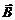 , возникает вихревое электрическое поле, направленное против тока I в контуре.
, возникает вихревое электрическое поле, направленное против тока I в контуре.
Задача 8
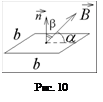 Квадратный проводящий контур со стороной b = 1 м пронизывает однородное магнитное поле под углом a = 30° к плоскости контура. Индукция магнитного поля меняется со временем по закону
Квадратный проводящий контур со стороной b = 1 м пронизывает однородное магнитное поле под углом a = 30° к плоскости контура. Индукция магнитного поля меняется со временем по закону 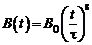 . Найти модуль э.д.с. индукции в контуре в момент времени t = 1 с, если
. Найти модуль э.д.с. индукции в контуре в момент времени t = 1 с, если 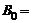 1 Тл; t = 1 с.
1 Тл; t = 1 с.
Решение:
Определим зависимость магниного потока от времени:
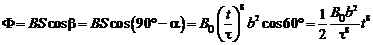
По формуле (6.2) определим модуль Э.Д.С. индукции:
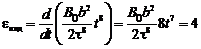 В
В
Ответ: 4 В
Задача 9
По проводящему контуру индуктивностью L течет ток I. Найти модуль э.д.с. самоиндукции в контуре в момент времени t = 1 с, если и ток и индуктивность изменяются со временем по законам 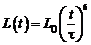 ,
, 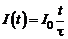 , где
, где 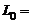 1 Гн;
1 Гн; 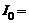 1А; t = 1 с.
1А; t = 1 с.
Решение:
Воспользуемся формулой (6.4):
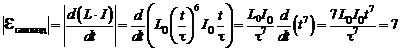 В.
В.
Ответ: 7 В.
Задача 10
 В однородном магнитном поле с индукцией В = 1 Тл по окружности летает положительно заряженная частица с зарядом q = 1 мкКл и массой m = 10–10кг со скоростью v = 10 км/с. Индукция магнитного поля
В однородном магнитном поле с индукцией В = 1 Тл по окружности летает положительно заряженная частица с зарядом q = 1 мкКл и массой m = 10–10кг со скоростью v = 10 км/с. Индукция магнитного поля 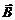 направлена вдоль оси z. В начальный момент времени скорость частицы
направлена вдоль оси z. В начальный момент времени скорость частицы 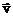 была направлена вдоль оси у. Найти минимальное время t, через которое скорость частицы будет направлена а) вдоль оси х; б) против оси х. Найти пройденный путь за это время.
была направлена вдоль оси у. Найти минимальное время t, через которое скорость частицы будет направлена а) вдоль оси х; б) против оси х. Найти пройденный путь за это время.
Решение:
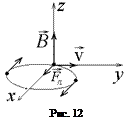
Из векторного выражения (7.1) следует, что сила Лоренца, действующая на частицу в начальный момент времени направлена вдоль оси х, поэтому частица будет двигаться так, как показано на рис.12. Из этого рисунка следует, что через четверть оборота или через время 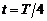 скорость частицы окажется направленной параллельно оси х, а через три четверти периода (
скорость частицы окажется направленной параллельно оси х, а через три четверти периода ( 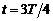 ) – антипараллельно оси х. Используя формулу для радиуса окружности (7.2) и периода (7.3), получаем ответ:
) – антипараллельно оси х. Используя формулу для радиуса окружности (7.2) и периода (7.3), получаем ответ:
а) 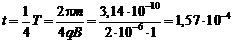 с;
с;
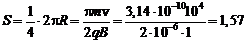 м.
м.
б) 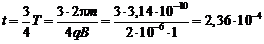 с
с
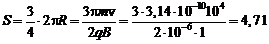 м.
м.
Ответы: а) t = 0,157 мс; S = 1,57 м; б) t = 0,236 мс; S = 4,71 м.
Задача 11
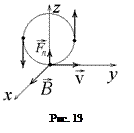 В однородном магнитном поле с индукцией В = 1 Тл по окружности летает отрицательно заряженная частица с зарядом q = – 1 мкКл и массой m = 10–10кг со скоростью v = 20 км/с. Индукция магнитного поля
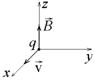
В однородном магнитном поле с индукцией В = 1 Тл по окружности летает отрицательно заряженная частица с зарядом q = – 1 мкКл и массой m = 10–10кг со скоростью v = 20 км/с. Индукция магнитного поля 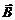 направлена вдоль оси х. В начальный момент времени скорость частицы
направлена вдоль оси х. В начальный момент времени скорость частицы 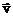 была направлена вдоль оси у. Найти минимальное время t, через которое скорость частицы будет направлена а) вдоль оси z; б) против оси z. Найти пройденный путь за это время.
была направлена вдоль оси у. Найти минимальное время t, через которое скорость частицы будет направлена а) вдоль оси z; б) против оси z. Найти пройденный путь за это время.
Решение:
Из векторного выражения (7.1) следует, что сила Лоренца, действующая на частицу в начальный момент времени направлена вдоль оси z, поэтому частица будет двигаться так, как показано на рис.13 Из этого рисунка следует, что через четверть оборота или через время 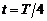 скорость частицы окажется направленной параллельно оси z, а через три четверти периода (
скорость частицы окажется направленной параллельно оси z, а через три четверти периода ( 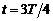 ) – антипараллельно оси z. Используя формулу для периода (7.3), получаем ответ:
) – антипараллельно оси z. Используя формулу для периода (7.3), получаем ответ:
а) 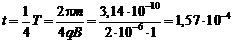 с;
с;
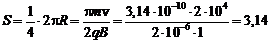 м.
м.
б) 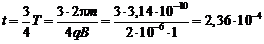 с
с
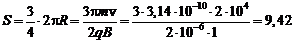 м.
м.
Ответы: а) t = 0,157 мс; S = 3,14 м; б) t = 0,236 мс; S = 9,42 м.
Плоский конденсатор
Разность потенциалов на обкладках плоского конденсатора, расстояние между которыми равно d и напряженность электрического поля Е:
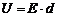 . (8.1)
. (8.1)
Энергия электрического поля в плоском конденсаторе, где С – емкость конденсатора, q – заряд на конденсаторе, U – напряжение на конденсаторе, Е – напряженность электрического поля:
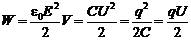 (8.2)
(8.2)
Напряженность однородного электрического поля внутри плоского конденсатора. 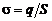 – поверхностная плотность заряда на обкладках плоского конденсатора:
– поверхностная плотность заряда на обкладках плоского конденсатора:
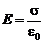 . (8.3)
. (8.3)
Уравнения Максвелла
Переменное магнитное поле с индукцией 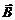 порождает в пространстве вихревое электрическое поле с напряженностью
порождает в пространстве вихревое электрическое поле с напряженностью 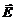 :
:
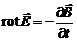 . (9.1)
. (9.1)
Вихревое магнитное поле с напряженностью 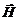 порождается в пространстве токами проводимости с плотностью
порождается в пространстве токами проводимости с плотностью 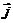 и переменным электрическим полем с индукцией
и переменным электрическим полем с индукцией 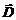 :
:
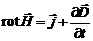 . (9.2)
. (9.2)
Материальное уравнение связывает вектор 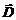 и
и 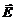 в изотропном диэлектрике:
в изотропном диэлектрике:
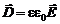 , (9.3)
, (9.3)
где e – диэлектрическая проницаемость среды ( 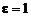 для воздуха),
для воздуха),
e0 = 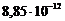 Ф/м– электрическая постоянная.
Ф/м– электрическая постоянная.
Задача 12
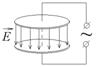 Между обкладками плоского воздушного конденстатора создано однородное электрическое поле, напряженность которого меняется со временем по закону
Между обкладками плоского воздушного конденстатора создано однородное электрическое поле, напряженность которого меняется со временем по закону 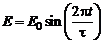 . Найти модуль ротора напряженности магнитного поля (или плотность тока смещения) внутри конденсатора в момент времени t = 1 с, если
. Найти модуль ротора напряженности магнитного поля (или плотность тока смещения) внутри конденсатора в момент времени t = 1 с, если 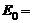 1 кВ/м;
1 кВ/м; 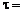 1 с.
1 с.
Решение:
Между обкладками конденсатора нет токов проводимости, т.е. 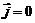 . Так как конденсатор воздушный, то диэлектрическая проницаемость среды e = 1, следовательно из формулы (9.3)
. Так как конденсатор воздушный, то диэлектрическая проницаемость среды e = 1, следовательно из формулы (9.3) 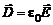 . По формуле (9.2) найдем модуль ротора
. По формуле (9.2) найдем модуль ротора 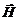 в момент времени t = 1 c:
в момент времени t = 1 c:
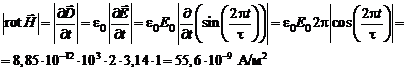
Ответ: 55,6 нА/м2
Задача 13
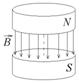 Между полюсами магнита создано однродное магнитное поле, индукция которого зависит от времени по закону
Между полюсами магнита создано однродное магнитное поле, индукция которого зависит от времени по закону 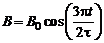 . Найти модуль ротора напряженности электрического поля между полюсами в момент времени t = 1 с, если
. Найти модуль ротора напряженности электрического поля между полюсами в момент времени t = 1 с, если 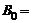 1 Тл;
1 Тл; 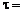 1 с.
1 с.
Решение:
По формуле (9.1) найдем модуль ротора 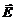 :
:
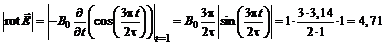 Тл/с
Тл/с
Ответ: 4,71 Тл/с
 10. Электрические колебания
10. Электрические колебания
Уравнение затухающих колебаний в контуре, состоящем из последовательно соединенных резистора с сопротивлением R, конденсатора с емкостью С и катушки с индуктивностью L, выглядит так:
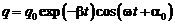 , (10.1)
, (10.1)
где b – коэффициент затухания:
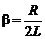 ; (10.2)
; (10.2)
w –– циклическая частота собственных затухающих колебаний.
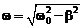 ; (10.3)
; (10.3)
w0 – циклическая частота собственных незатухающих колебаний.
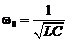 (10.4)
(10.4)
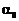 – начальная фаза колебаний,
– начальная фаза колебаний, 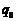 – начальная амплитуда.
– начальная амплитуда.
Амплитуда колебаний в контуре уменьшается со временем по закону:
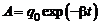 . (10.5)
. (10.5)
q – логарифмический декремент затухания:
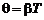 . (10.6)
. (10.6)
t –– время релаксации (время, за которое амплитуда уменьшится в е = 2,72 раз)
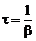 . (10.7)
. (10.7)
Задача 14
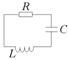 В контуре совершаются свободные слабозатухающие колебания, при которых заряд на конденсаторе изменяется во времени по закону
В контуре совершаются свободные слабозатухающие колебания, при которых заряд на конденсаторе изменяется во времени по закону 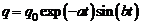 . Оцените время, через которое энергия контура уменьшится в 2раза.
. Оцените время, через которое энергия контура уменьшится в 2раза. 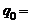 1 мкКл;
1 мкКл; 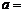 0,05 с–1;
0,05 с–1; 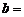 10 c–1. Каким станет коэффициент затухания, если:
10 c–1. Каким станет коэффициент затухания, если:
а) сопротивление R в контуре увеличить в 2 раза?
б) индуктивность L в контуре увеличить в 2 раза?
в) емкость С в контуре увеличить в 2 раза?
Решение:
Энергия контура W пропорциональна квадрату амплитуды колебаний, поэтому, используя формулу (10.5) и учитывая, что b = а = 0,05 с–1, получим:
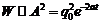 (10.8)
(10.8)
Найдем отношение энергий контура в начальный момент времени и в момент времени t:
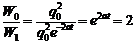 . (10.9)
. (10.9)
Из формулы (10.9) видно, что 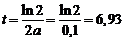 с
с
из формулы (10.2) следует, что
а) если сопротивление в контуре увеличить в два раза, то коэффициент затухания увеличится также в два раза: 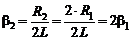 = 0,1 с–1;
= 0,1 с–1;
б) при изменении индуктивности в два раза, коэффициент затухания уменьшится в два раза: 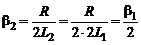 = 0,025 с–1;
= 0,025 с–1;
в) при изменении емкости в два раза коэффициент затухания не изменится, так как он не зависит от емкости С (см. формулу (10.2)).
Ответы:t = 6,93 c; а) b = 0,1 с–1; б) b = 0,025 с–1; в) b = 0,05 с–1.
Расчет силы тока через поперечное сечение проводника.
Если ток протекает через площадь 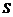 произвольной формы, то силу тока можно рассчитать по формуле
произвольной формы, то силу тока можно рассчитать по формуле
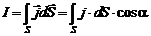 , (1.1)
, (1.1)
где вектор 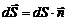 , а
, а 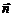 – это единичный вектор нормали к площадке
– это единичный вектор нормали к площадке 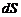 ; a – угол между векторами
; a – угол между векторами 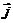 и
и 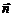 .
.
Если проводник сделан в виде тонкой полосы, и известна линейная плотность тока i, то полный ток можно найти по формуле:
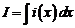 , (1.2)
, (1.2)
где dx – ширина полоски, вдоль которой течет ток dI
(см. рис. к задаче 3).
Задача 1
 По неоднородному цилиндрическому проводу радиуса R = 1 м течет ток. Найдите силу тока, протекающего через поперечное сечение проводника, если зависимость плотности тока от расстояния r до оси задается формулой
По неоднородному цилиндрическому проводу радиуса R = 1 м течет ток. Найдите силу тока, протекающего через поперечное сечение проводника, если зависимость плотности тока от расстояния r до оси задается формулой 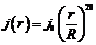 , где
, где 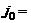 1 А/м2.
1 А/м2.
 Решение:
Решение:
Разобъем поперечное сечение проводника (круг радиуса R) на кольца радиуса r и шириной dr (см. рис.1). Площадь такого кольца равна 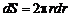 , а угол a между
, а угол a между 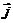 и
и 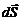 равен 0°. Используя формулу (1.1), найдем полный ток, протекающий через все поперечное сечение проводника:
равен 0°. Используя формулу (1.1), найдем полный ток, протекающий через все поперечное сечение проводника:
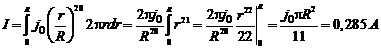
Ответ: I = 0,285 A
Задача 2
 По неоднородному проводу квадратного сечения
По неоднородному проводу квадратного сечения 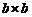 течет ток. Найдите силу тока, протекающего через поперечное сечение проводника, если плотность тока зависит от расстояния x от одной из боковых граней по закону
течет ток. Найдите силу тока, протекающего через поперечное сечение проводника, если плотность тока зависит от расстояния x от одной из боковых граней по закону 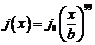 , где
, где 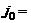 1 А/м2; b = 1 м.
1 А/м2; b = 1 м.
 Решение:
Решение:
Разобъем поперечное сечение проводника (квадрат 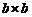 ) на узкие полоски шириной
) на узкие полоски шириной 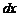 и высотой b (см. рис.2). Площадь такой полоски равна
и высотой b (см. рис.2). Площадь такой полоски равна 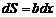 а угол a между
а угол a между 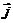 и
и 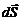 равен 0°. Используя формулу (1.1), найдем полный ток, протекающий через все поперечное сечение проводника:
равен 0°. Используя формулу (1.1), найдем полный ток, протекающий через все поперечное сечение проводника:
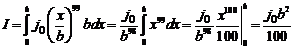
Ответ: I = 0,01 A
Задача 3
 Вдоль средней линии проводящей полосы шириной 2b течет ток. Найдите силу тока, протекающего по всей полосе, если линейная плотность тока зависит от расстояния x до средней линии по закону
Вдоль средней линии проводящей полосы шириной 2b течет ток. Найдите силу тока, протекающего по всей полосе, если линейная плотность тока зависит от расстояния x до средней линии по закону 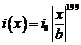 , где
, где 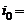 1 А/м; b = 1 м.
1 А/м; b = 1 м.
Решение:
Выделим на плоскости параллельно средней линии на расстоянии х узкую полоску шириной dx (см. рис.3). Используя формулу (1.2) найдем полный ток: 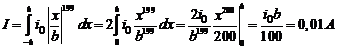
Ответ:I = 0,01 А
