Дайте определение понятия намагниченности. Какой физический процесс описывает уравнение Блоха (при отсутствии диссипации.)

Намагниченность.Сумма магнитных моментов ядер, прецессирующих вокруг направления внешнего магнитного поля, эквивалентна единственному магнитному моменту, макроскопической намагниченностью. Она отображает общую намагниченность, обусловленную разностью населенностей, т.е. избытком ядер на нижнем энергетическом уровне при состоянии устойчивого равновесия.

Применим к уравнению (3.4) операцию осреднения по ансамблю диполей:

, (3.7)

где — бесконечно малая область, содержащая в то же время достаточно большое число магнитных диполей — так, чтобы величину можно было считать непрерывной или кусочно - непрерывной функцией координат. Функция называется намагниченностью вещества и в общем случае она зависит не только от пространственных координат, но и от времени и отражает реакцию вещества на приложение внешнего магнитного поля.

Результат применения операции осреднения (с учетом введенных обозначений) к уравнению (3.4) оказывается следующим:

, (3.8)

Полученное уравнение называется уравнением Блоха.

Найдем, используя уравнения Блоха, какой эффект окажет поле (4.18) на вектор намагниченности . Заметим, прежде всего, что обычно длительность высокочастотного импульса не превышает 2 мс, тогда как самое короткое время релаксации не менее 40 мс. Следовательно, для времен, не превышающих 40 мс, диссипацией можно пренебречь и использовать уравнения (3.8):

, (4.19)

При включении высокочастотного поля будем иметь:

(4.20)

Используя выражение (4.19) для внешнего поля, запишем уравнение (4.19) в компонентах:

,

, (4.21)

При произвольной зависимости точное решение уравнений (4.21) построить нельзя, однако в случае, когда

(4.22)

такое решение построить можно.

Предположим дополнительно, что , и перейдем к новым искомым функциям и с помощью замены

, , (4.23)

Из формул (4.23) видно, что величина равна проекции вектора намагниченности 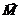на ось декартовой системы координат, вращающейся около оси с угловой скоростью 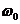, величина равна проекции вектора 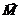на ось той же координатной системы ( ).

Подстановка выражений (4.23) в уравнения (4.21) приводит к следующей простой системе уравнений:

, , (4.24)

Примем следующие начальные условия:

, , (4.25)

где — равновесное значение вектора намагниченности 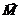при отсутствии высочастотного возбуждения.

Решение системы (4.24) с начальными условиями (4.25) имеет вид:

, , (4.26)

Таким образом, в подвижной системе координат вектор вращается около оси оставаясь в плоскости с угловой скоростью . Угол поворота за время будет равен

, (4.27)

По причинам, о которых речь пойдет ниже, импульс высокочастотного возбуждения выбирают таким, чтобы угол 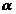оказался равным или .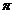

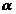Отметим в заключение этого п.п., что в случае, когда —импульс конечной длительности , угол поворота приближенно можно определить по формуле

, (4.28)

Этот результат устанавливается методами теории возмущений.

17.Дайте определение понятия релаксации. Какие явления характеризуют времена и .

Из эксперимента известно, что вектор с ростом стремится по направлению к вектору магнитной индукции , причем этот процесс, называемый релаксацией (точнее релаксация — процесс возвращения спина ядра атома к равновесному состоянию), имеет два характерных времени и . Времена и характеризуют связи ядер атомов с решеткой. Время характеризует процесс уменьшения компонентов , до нуля и называется временем спин - спиновой или поперечной релаксации. Время определяет стремление к нулю разности , где — равновесное значение, установившееся в течение большого промежутка времени после поворота, характеризует пространственное распределение релаксирующих ядер. Величина называется временем спин - решеточной или продольной релаксации; во всех известных случаях .

Опишите явление МР.

Пусть образец некоторого материала (техническая конструкция или пациент) помещен в постоянное магнитное поле. Через некоторый промежуток времени, зависящий от вида материала, магнитные спины образца сориентируются по полю. Для того, чтобы получить характеристики материала образца необходимо, прежде всего, вывести весь образец или какую - либо его часть из равновесного состояния. Снимая или меняя возмущающее воздействие, можно получить (измерить) отклик – сигнал. В частности, при полном снятии возбуждения откликом будет переменное электромагнитное поле, сопровождающее прецессию, описываемую формулами (3.13).

Явление ЯМР связано с поведением в магнитном поле магнитных моментов атомных ядер. Ядро атом состоит из протонов и нейтронов. Все частицы постоянно вращаются вокруг своей оси и обладают, поэтому собственным моментом количества движения - спином s. При этом собственный положительный заряд протона вращается вместе с ним и создает по закону электромагнитной индукции собственное магнитное поле. Таким образом, собственное магнитное поле протона похоже на поле постоянного магнита и представляет собой магнитный диполь с северным и южным полюсами. Когда пациента помещают внутрь сильного магнитного поля МР - томографа, все маленькие протонные магниты тела разворачиваются в направлении внешнего поля. Помимо этого, магнитные оси каждого протона начинают вращаться вокруг направления внешнего магнитного поля. Это специфическое вращение называется прецессией, а его частоту - резонансной частотой или частотой Лармора. Частота Л. пропорциональна силе внешнего магнитного поля и составляет для ядер атома водорода 42,58 МГц/Тс.