Объясните с механической точки зрения уравнение Лармора. Дайте определение ларморовой частоты и ее значение для задач диагностики.
Атомные ядра обладают электрическим зарядом. Ядра некоторых атомов обладают моментом количества движения (угловым моментом) 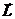 . Таким свойством обладают ядра с нечетным числом нуклонов (протонов и нейтронов). Последние обладают магнитными свойствами, которые превращают каждое такое ядро в магнитный диполь, имеющий определённую ориентацию. Подобных ядер достаточно много, и к ним, в частности, относятся протоны, составляющие 99,98 % всех атомов водорода в природе, углерод—13 и фосфор—31%.). Вращение электрически заряженного ядра вокруг центральной оси под действием углового момента приводит к появлению магнитного поля, характеризуемого магнитным дипольным моментом
. Таким свойством обладают ядра с нечетным числом нуклонов (протонов и нейтронов). Последние обладают магнитными свойствами, которые превращают каждое такое ядро в магнитный диполь, имеющий определённую ориентацию. Подобных ядер достаточно много, и к ним, в частности, относятся протоны, составляющие 99,98 % всех атомов водорода в природе, углерод—13 и фосфор—31%.). Вращение электрически заряженного ядра вокруг центральной оси под действием углового момента приводит к появлению магнитного поля, характеризуемого магнитным дипольным моментом 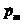 (магнитным диполем или спином). Магнитный дипольный момент
(магнитным диполем или спином). Магнитный дипольный момент 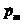 направлен противоположно вектору углового момента и перпендикулярно плоскости циркуляции заряда, как показано на рис. 2.
направлен противоположно вектору углового момента и перпендикулярно плоскости циркуляции заряда, как показано на рис. 2.
Имеет место формула:
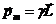 . (3.1)
. (3.1)
коэффициент пропорциональности 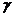 в которой называется гиромагнитным отношением. Для протона (ядра атома водорода)
в которой называется гиромагнитным отношением. Для протона (ядра атома водорода)
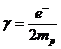 . (3.2)
. (3.2)
где 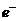 — элементарный заряд (заряд электрона),
— элементарный заряд (заряд электрона), 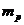 — масса протона.
— масса протона.
Выведем уравнения, описывающие поведение отдельного магнитного диполя (спина), используя для этого законы классической механики.
Будем рассматривать магнитный диполь как вращающееся абсолютно твердое тело. По теореме об изменении количества движения скорость изменения величины 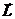 равна сумме моментов всех действующих на вращающееся тело сил. В соответствии с формулой (1.21) момент сил, действующих на диполь, равен
равна сумме моментов всех действующих на вращающееся тело сил. В соответствии с формулой (1.21) момент сил, действующих на диполь, равен 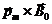 , где
, где 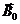 — магнитная индукция в рассматриваемой точке пространства. Следовательно, теорема об изменении количества движения позволяет написать следующее уравнение:
— магнитная индукция в рассматриваемой точке пространства. Следовательно, теорема об изменении количества движения позволяет написать следующее уравнение:
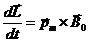 , (3.3)
, (3.3)
Учитывая формулу (3.1), приходим к уравнению:
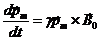 , (3.4)
, (3.4)
вполне аналогичному уравнению движения абсолютно твердого тела с одной неподвижной точкой в поле сил тяжести, когда положение центра тяжести не совпадает с неподвижной точкой. Используя установленную аналогию, заключаем, что роль вектора, идущего из неподвижной точки 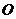 в центр тяжести
в центр тяжести 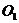 играет вектор
играет вектор 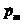 , силе тяжести соответствует вектор
, силе тяжести соответствует вектор 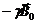 . Если этот вектор противоположен по направлению оси
. Если этот вектор противоположен по направлению оси 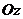 некоторой неподвижной декартовой системы отсчета, то вектор
некоторой неподвижной декартовой системы отсчета, то вектор 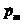 будет двигаться по поверхности кругового конуса или — по терминологии, используемой в теории гироскопа, совершать прецессию. Угловая скорость (вектор) прецессии в рамках приближенной теории гироскопа равна:
будет двигаться по поверхности кругового конуса или — по терминологии, используемой в теории гироскопа, совершать прецессию. Угловая скорость (вектор) прецессии в рамках приближенной теории гироскопа равна:
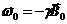 (3.5)
(3.5)
и направлена по оси конуса. Частота
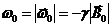 (3.6)
(3.6)
называется ларморовой частотой. Для того, чтобы сохранить общепринятое правило отсчета положительных углов поворота, в дальнейшем в определении (3.6) правую часть будем брать со знаком минус. Ее наиболее важное для задач диагностики свойство заключается в том, что она прямо пропорциональна индукции внешнего магнитного поля 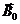 . Очевидно, что, меняя
. Очевидно, что, меняя 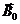 , можно управлять частотой прецессии
, можно управлять частотой прецессии 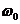 . В частности, если
. В частности, если 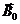 будет зависеть от координат, то можно локализовать области в теле с заданной частотой. Ларморова частота нужна для регистрации разных хим. элементов.
будет зависеть от координат, то можно локализовать области в теле с заданной частотой. Ларморова частота нужна для регистрации разных хим. элементов.
