Источники и стоки точечных дефектов

Основным источником и стоком точечных дефектов являются линейные и поверхностные дефекты — см. ниже. В крупных совершенных монокристаллах возможен распад пересыщенного твердого раствора собственных точечных дефектов с образованием т. н. микродефектов.

Б) Одномерные дефекты

Одномерные (линейные) дефекты представляют собой дефекты кристалла, размер которых по одному направлению много больше параметра решетки, а по двум другим — соизмерим с ним. К линейным дефектам относят дислокации идисклинации. Общее определение: дислокация — граница области незавершенного сдвига в кристалле. Дислокации характеризуются вектором сдвига (вектором Бюргерса) и углом φ между ним и линией дислокации. При φ=0 дислокация называется винтовой; при φ=90° — краевой; при других углах — смешанной и тогда может быть разложена на винтовую и краевую компоненты. Дислокации возникают в процессе роста кристалла; при его пластической деформации и во многих других случаях. Их распределение и поведение при внешних воздействиях определяют важнейшие механические свойства, в частности такие как прочность, пластичность и др. Дисклинация — граница области незавершенного поворота в кристалле. Характеризуется вектором поворота.

В) Двумерные Дефекты

Основной дефект-представитель этого класса — поверхность кристалла. Другие случаи — границы зёрен материала, в том числе малоугловые границы (представляют собой ассоциации дислокаций), плоскостидвойникования, поверхности раздела фаз и др

Г) Трёхмерные дефекты

Объёмные дефекты. К ним относятся скопления вакансий, образующие поры и каналы; частицы, оседающие на различных дефектах (декорирующие), например пузырьки газов, пузырьки маточного раствора; скопления примесей в виде секторов (песочных часов) и зон роста. Как правило, это поры или включения примесных фаз. Представляют собой конгломерат из многих дефектов. Происхождение — нарушение режимов роста кристалла, распад пересыщенного твердого раствора, загрязнение образцов. В некоторых случаях (например, при дисперсионном твердении) объемные дефекты специально вводят в материал, для модификации его физических свойств.

2) Механизм Образования Вакансии.

(Частично см предыдущий ответ)

Точечный дефект кристаллической решётки, являющий собой отсутствие атома в узле решётки.

Выделяется два механизма образования:
а) по Шоттки - образование вакансии в поверхностном слое атомов, когда атом из узла решётки выходит, как бы, на слой выше поверхностного, после чего вакансия может уйти вглубь кристалла;

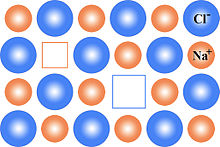
б) по Френкелю - одновременное образование вакансии и междоузельного атома, когда атом, вследствие теплового движения, покидает своё место в решётке и оказывается в междоузлии.

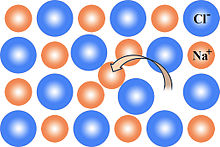
3) Дислокации и их образование

Дислока́ции

в кристаллах, дефекты кристалла, представляющие собой линии, вдоль и вблизи которых нарушено характерное для кристалла правильное расположение атомных плоскостей. Д. и другие Дефекты в кристаллах определяют многие физические свойства кристаллов, называемые структурно-чувствительными. В частности, механические свойства кристаллов — прочность и пластичность — обусловлены существованием Д. и их особенностями.

Типы Д. Простейшими видами Д. являются краевая и винтовая Д. В идеальном кристалле (См. Идеальный кристалл) соседние атомные плоскости параллельны на всём своём протяжении. В реальном кристалле атомные плоскости часто обрываются внутри кристалла (рис. 1, а), при этом возникает краевая Д., осью которой является край «лишней» полуплоскости. Применение электронных микроскопов (См. Электронный микроскоп) с большой разрешающей способностью позволяет наблюдать в некоторых кристаллах специфичное для краевой Д. расположение атомных рядов.

Образование краевой Д. можно представить себе, если надрезать кристалл по части плоскости ABCD (рис. 1, б), сдвинуть нижнюю часть относительно верхней на одно межатомное расстояние b в направлении, перпендикулярном к АВ, а затем вновь соединить атомы на противоположных краях разреза. Оставшаяся лишняя полуплоскость обрывается вдоль краевой Д. АВ. Вектор b, величина которого равна межатомному расстоянию, называется вектором сдвига (вектор Бюргерса). Плоскость, проходящая через вектор сдвига и линию Д., называется плоскостью скольжения краевой Д.

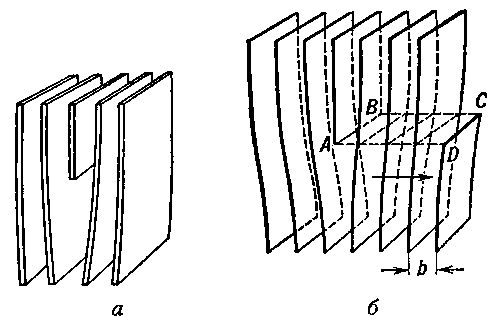
Рис. 1. Краевая дислокация: а — обрыв атомной плоскости внутри кристалла; б — схема образования краевой дислокации.

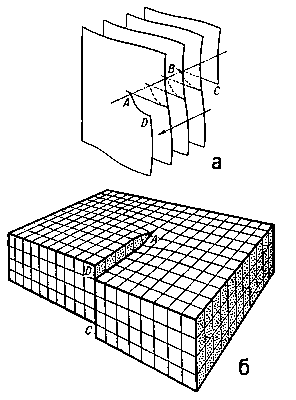
Рис. 2. Винтовая дислокация: а — схема образования винтовой дислокации; б — расположение атомов в кристалле с винтовой дислокацией (атомы располагаются в вершинах кубиков).

3.

1) Нормальные колебания в решетке

(от сюда надо выдержанно взять инфу, но для понимая стоит прочесть всё)

Колебания кристаллической решётки

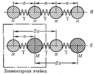
Колебания кристаллической решётки, один из основных видов внутренних движений твёрдого тела, при котором составляющие его частицы (атомы или ионы) колеблются около положений равновесия — узлов кристаллической решётки. К. к. р., например, в виде стоячих или бегущих звуковых волн возникают всякий раз, когда на кристалл действует внешняя сила, изменяющаяся со временем. Однако и в отсутствие внешних воздействий в кристалле, находящемся в тепловом равновесии с окружающей средой, устанавливается стационарное состояние колебаний, подобно тому как в газе устанавливается стационарное распределение атомов или молекул по скорости их поступательного движения.

Характер этих колебаний зависит от симметрии кристалла, числа атомов в его элементарной ячейке, типа химической связи, а также от вида и концентрации дефектов в кристаллах. Смещения и атомов в процессе колебаний тем больше, чем выше температура, но они гораздо меньше постоянной решетки вплоть до температуры плавления, когда твердое тело превращается в жидкость. Силы, которые стремятся удержать атомы в положениях равновесия, пропорциональны их относительным смещениям так, как если бы они были связаны друг с другом пружинками (рис. 1). Представление кристалла в виде совокупности частиц, связанных идеально упругими силами, называется гармоническим приближением.

В кристалле, состоящем из N элементарных ячеек по n атомов в каждой, существует 3nN — 6 типов простейших колебаний в виде стоячих волн, называемых нормальными (либо собственными) колебаниями, или модами. Их число равно числу степеней свободы у совокупности частиц кристалла за вычетом трёх степеней свободы, отвечающих поступательному, и трёх — вращательному движению кристалла как целого (см.Степеней свободы число). Числом 6 можно пренебречь, так как 3nN — величина ~ 10²²—10²³ для 1 см³ кристалла.

В процессе нормального колебания все частицы кристалла колеблются около своих положений равновесия с одной и той же постоянной частотой w по закону u ~ sinw·t подобно простому гармоническому осциллятору. В кристалле одновременно могут присутствовать все возможные нормальные колебания, причем каждое протекает так, как если бы остальных не было вовсе. Любое движение атомов в кристалле, не нарушающее его микроструктуры, может быть представлено в виде суперпозиции нормальных колебаний кристалла.

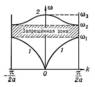
Каждую стоячую волну нормального колебания можно, в свою очередь, представить в виде двух упругих плоских бегущих волн, распространяющихся в противоположных направлениях (нормальные волны). Плоская бегущая волна, помимо частоты w, характеризуется волновым вектором k, определяющим направление движения фронта волны и длину волны l= 2 p/k, а также поляризацией, которая определяет характер индивидуального движения частиц. В общем случае имеет место эллиптическая поляризация, когда каждый атом описывает эллипс около своего положения равновесия (рис. 2), при этом нормаль к плоскости эллипса не совпадает по направлению с k. Эллиптические орбиты одинаковы для идентичных атомов, занимающих эквивалентные положения в решётке. В тех кристаллах, где каждый узел является центром симметрии (см. Симметрия кристаллов), все нормальные волны плоскополяризованы: атомы в любом нормальном колебании совершают возвратно-поступательные движения около своих положений равновесия.

Дисперсия нормальных волн. При каждом значении k существует 3n типов нормальных волн с различной поляризацией. Они нумеруются целочисленной переменной s = 1, 2... 3n и называется ветвями нормальных колебаний. Для волн данного типа s величины w и k не могут быть произвольными, а связаны между собой определённым соотношением w = w(k, s), называется законом дисперсии. Например, если представить кристалл в виде совокупности одинаковых атомов массы т, расположенных на равных расстояниях а друг от друга и связанных попарно пружинами с жёсткостью g так, что они образуют бесконечную цепочку и могут смещаться только вдоль её оси (рис. 3, а), то элементарная ячейка состоит из одной частицы и существует одна ветвь частоты нормальных колебаний с законом дисперсии:

.

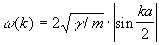У двухатомной линейной цепочки (рис. 3, б) ячейка содержит 2 частицы с массами т и М и имеется 2 ветви с более сложным законом дисперсии (рис. 4): 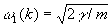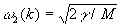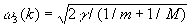_{, ,} , (M > m).

Упругие волны в кристалле всегда обладают дисперсией. В частности, их фазовая скорость, как правило, отличается от групповой, с которой по кристаллу переносится энергия колебаний. В то время как частота w упругих волн, распространяющихся в непрерывной среде, неограниченно возрастает с ростом k, в кристалле благодаря периодическому расположению атомов и конечной величине связывающих их сил существует некоторая максимальная частота колебаний w_макс (обычно ~10¹³гц). Собственные частоты могут не сплошь заполнять интервал от w = 0 до w =w_макс, в нём могут быть пустые участки (запрещенные зоны), разделяющие две следующие друг за другом ветви. Запрещенной зоны между соседними ветвями нет, если ветви перекрываются. Колебания, соответствующие запрещенным зонам и с частотой w > w_макс, не могут распространяться в кристалле, они быстро затухают.

2) спектр Нормальных колебаний решётки и температура дебая

Температура Дебая — температура, при которой возбуждаются все моды колебаний в данном твёрдом теле. Дальнейшее увеличение температуры не приводит к появлению новых мод колебаний, а лишь ведёт к увеличению амплитуд уже существующих, то есть средняя энергия колебаний с ростом температуры растёт.

Температура Дебая — физическая константа вещества, характеризующая многие свойства твёрдых тел — теплоёмкость, электропроводность, теплопроводность, уширение линий рентгеновских спектров, упругие свойства и т. п. Введена впервые П. Дебаем в его теории теплоёмкости.

Температура Дебая определяется следующей формулой:

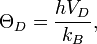
где 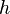— постоянная Планка, 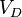— максимальная частота колебаний атомов твёрдого тела, 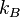— постоянная Больцмана.

Температура Дебая приближённо указывает температурную границу, ниже которой начинают сказываться квантовые эффекты.

А вот со спектром у меня никак отношения не складываются. НО. Вроде там чем больше температура, тем больше спектр колебаний. Естессно до температуры Дебая, там, как сказано выше, амплитуда увеличивается только.

3) Температурная зависимость теплоёмкости по Эйнштейну и по Дебаю

Тут будет много формул, лично я пробежался только по теории. Кратко - эйнштейн был не совсем прав, дебай правильнее сформулировал.