Приближение почти свободных электронов. Модель Кронига–Пенни

Источники и стоки точечных дефектов

Основным источником и стоком точечных дефектов являются линейные и поверхностные дефекты — см. ниже. В крупных совершенных монокристаллах возможен распад пересыщенного твердого раствора собственных точечных дефектов с образованием т. н. микродефектов.

Б) Одномерные дефекты

Одномерные (линейные) дефекты представляют собой дефекты кристалла, размер которых по одному направлению много больше параметра решетки, а по двум другим — соизмерим с ним. К линейным дефектам относят дислокации идисклинации. Общее определение: дислокация — граница области незавершенного сдвига в кристалле. Дислокации характеризуются вектором сдвига (вектором Бюргерса) и углом φ между ним и линией дислокации. При φ=0 дислокация называется винтовой; при φ=90° — краевой; при других углах — смешанной и тогда может быть разложена на винтовую и краевую компоненты. Дислокации возникают в процессе роста кристалла; при его пластической деформации и во многих других случаях. Их распределение и поведение при внешних воздействиях определяют важнейшие механические свойства, в частности такие как прочность, пластичность и др. Дисклинация — граница области незавершенного поворота в кристалле. Характеризуется вектором поворота.

В) Двумерные Дефекты

Основной дефект-представитель этого класса — поверхность кристалла. Другие случаи — границы зёрен материала, в том числе малоугловые границы (представляют собой ассоциации дислокаций), плоскостидвойникования, поверхности раздела фаз и др

Г) Трёхмерные дефекты

Объёмные дефекты. К ним относятся скопления вакансий, образующие поры и каналы; частицы, оседающие на различных дефектах (декорирующие), например пузырьки газов, пузырьки маточного раствора; скопления примесей в виде секторов (песочных часов) и зон роста. Как правило, это поры или включения примесных фаз. Представляют собой конгломерат из многих дефектов. Происхождение — нарушение режимов роста кристалла, распад пересыщенного твердого раствора, загрязнение образцов. В некоторых случаях (например, при дисперсионном твердении) объемные дефекты специально вводят в материал, для модификации его физических свойств.

2) Механизм Образования Вакансии.

(Частично см предыдущий ответ)

Точечный дефект кристаллической решётки, являющий собой отсутствие атома в узле решётки.

Выделяется два механизма образования:
а) по Шоттки - образование вакансии в поверхностном слое атомов, когда атом из узла решётки выходит, как бы, на слой выше поверхностного, после чего вакансия может уйти вглубь кристалла;

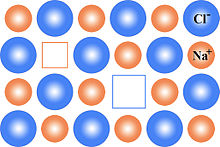
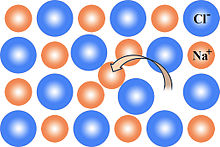
б) по Френкелю - одновременное образование вакансии и междоузельного атома, когда атом, вследствие теплового движения, покидает своё место в решётке и оказывается в междоузлии.

3) Дислокации и их образование

Дислока́ции

в кристаллах, дефекты кристалла, представляющие собой линии, вдоль и вблизи которых нарушено характерное для кристалла правильное расположение атомных плоскостей. Д. и другие Дефекты в кристаллах определяют многие физические свойства кристаллов, называемые структурно-чувствительными. В частности, механические свойства кристаллов — прочность и пластичность — обусловлены существованием Д. и их особенностями.

Типы Д. Простейшими видами Д. являются краевая и винтовая Д. В идеальном кристалле (См. Идеальный кристалл) соседние атомные плоскости параллельны на всём своём протяжении. В реальном кристалле атомные плоскости часто обрываются внутри кристалла (рис. 1, а), при этом возникает краевая Д., осью которой является край «лишней» полуплоскости. Применение электронных микроскопов (См. Электронный микроскоп) с большой разрешающей способностью позволяет наблюдать в некоторых кристаллах специфичное для краевой Д. расположение атомных рядов.

Образование краевой Д. можно представить себе, если надрезать кристалл по части плоскости ABCD (рис. 1, б), сдвинуть нижнюю часть относительно верхней на одно межатомное расстояние b в направлении, перпендикулярном к АВ, а затем вновь соединить атомы на противоположных краях разреза. Оставшаяся лишняя полуплоскость обрывается вдоль краевой Д. АВ. Вектор b, величина которого равна межатомному расстоянию, называется вектором сдвига (вектор Бюргерса). Плоскость, проходящая через вектор сдвига и линию Д., называется плоскостью скольжения краевой Д.

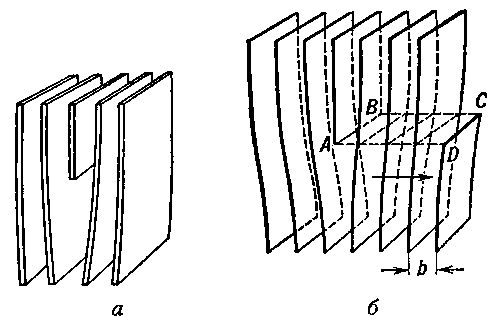
Рис. 1. Краевая дислокация: а — обрыв атомной плоскости внутри кристалла; б — схема образования краевой дислокации.

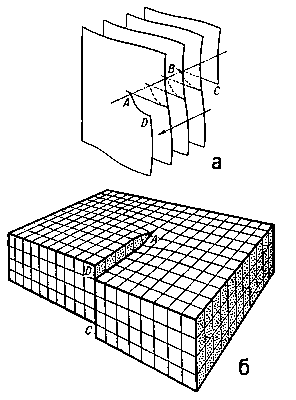
Рис. 2. Винтовая дислокация: а — схема образования винтовой дислокации; б — расположение атомов в кристалле с винтовой дислокацией (атомы располагаются в вершинах кубиков).

3.

1) Нормальные колебания в решетке

(от сюда надо выдержанно взять инфу, но для понимая стоит прочесть всё)

Колебания кристаллической решётки

Колебания кристаллической решётки, один из основных видов внутренних движений твёрдого тела, при котором составляющие его частицы (атомы или ионы) колеблются около положений равновесия — узлов кристаллической решётки. К. к. р., например, в виде стоячих или бегущих звуковых волн возникают всякий раз, когда на кристалл действует внешняя сила, изменяющаяся со временем. Однако и в отсутствие внешних воздействий в кристалле, находящемся в тепловом равновесии с окружающей средой, устанавливается стационарное состояние колебаний, подобно тому как в газе устанавливается стационарное распределение атомов или молекул по скорости их поступательного движения.

Характер этих колебаний зависит от симметрии кристалла, числа атомов в его элементарной ячейке, типа химической связи, а также от вида и концентрации дефектов в кристаллах. Смещения и атомов в процессе колебаний тем больше, чем выше температура, но они гораздо меньше постоянной решетки вплоть до температуры плавления, когда твердое тело превращается в жидкость. Силы, которые стремятся удержать атомы в положениях равновесия, пропорциональны их относительным смещениям так, как если бы они были связаны друг с другом пружинками (рис. 1). Представление кристалла в виде совокупности частиц, связанных идеально упругими силами, называется гармоническим приближением.

В кристалле, состоящем из N элементарных ячеек по n атомов в каждой, существует 3nN — 6 типов простейших колебаний в виде стоячих волн, называемых нормальными (либо собственными) колебаниями, или модами. Их число равно числу степеней свободы у совокупности частиц кристалла за вычетом трёх степеней свободы, отвечающих поступательному, и трёх — вращательному движению кристалла как целого (см.Степеней свободы число). Числом 6 можно пренебречь, так как 3nN — величина ~ 10²²—10²³ для 1 см³ кристалла.

В процессе нормального колебания все частицы кристалла колеблются около своих положений равновесия с одной и той же постоянной частотой w по закону u ~ sinw·t подобно простому гармоническому осциллятору. В кристалле одновременно могут присутствовать все возможные нормальные колебания, причем каждое протекает так, как если бы остальных не было вовсе. Любое движение атомов в кристалле, не нарушающее его микроструктуры, может быть представлено в виде суперпозиции нормальных колебаний кристалла.

Каждую стоячую волну нормального колебания можно, в свою очередь, представить в виде двух упругих плоских бегущих волн, распространяющихся в противоположных направлениях (нормальные волны). Плоская бегущая волна, помимо частоты w, характеризуется волновым вектором k, определяющим направление движения фронта волны и длину волны l= 2 p/k, а также поляризацией, которая определяет характер индивидуального движения частиц. В общем случае имеет место эллиптическая поляризация, когда каждый атом описывает эллипс около своего положения равновесия (рис. 2), при этом нормаль к плоскости эллипса не совпадает по направлению с k. Эллиптические орбиты одинаковы для идентичных атомов, занимающих эквивалентные положения в решётке. В тех кристаллах, где каждый узел является центром симметрии (см. Симметрия кристаллов), все нормальные волны плоскополяризованы: атомы в любом нормальном колебании совершают возвратно-поступательные движения около своих положений равновесия.

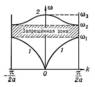
Дисперсия нормальных волн. При каждом значении k существует 3n типов нормальных волн с различной поляризацией. Они нумеруются целочисленной переменной s = 1, 2... 3n и называется ветвями нормальных колебаний. Для волн данного типа s величины w и k не могут быть произвольными, а связаны между собой определённым соотношением w = w(k, s), называется законом дисперсии. Например, если представить кристалл в виде совокупности одинаковых атомов массы т, расположенных на равных расстояниях а друг от друга и связанных попарно пружинами с жёсткостью g так, что они образуют бесконечную цепочку и могут смещаться только вдоль её оси (рис. 3, а), то элементарная ячейка состоит из одной частицы и существует одна ветвь частоты нормальных колебаний с законом дисперсии:

.

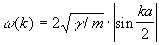У двухатомной линейной цепочки (рис. 3, б) ячейка содержит 2 частицы с массами т и М и имеется 2 ветви с более сложным законом дисперсии (рис. 4): 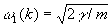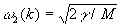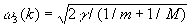_{, ,} , (M > m).

Упругие волны в кристалле всегда обладают дисперсией. В частности, их фазовая скорость, как правило, отличается от групповой, с которой по кристаллу переносится энергия колебаний. В то время как частота w упругих волн, распространяющихся в непрерывной среде, неограниченно возрастает с ростом k, в кристалле благодаря периодическому расположению атомов и конечной величине связывающих их сил существует некоторая максимальная частота колебаний w_макс (обычно ~10¹³гц). Собственные частоты могут не сплошь заполнять интервал от w = 0 до w =w_макс, в нём могут быть пустые участки (запрещенные зоны), разделяющие две следующие друг за другом ветви. Запрещенной зоны между соседними ветвями нет, если ветви перекрываются. Колебания, соответствующие запрещенным зонам и с частотой w > w_макс, не могут распространяться в кристалле, они быстро затухают.

2) спектр Нормальных колебаний решётки и температура дебая

Температура Дебая — температура, при которой возбуждаются все моды колебаний в данном твёрдом теле. Дальнейшее увеличение температуры не приводит к появлению новых мод колебаний, а лишь ведёт к увеличению амплитуд уже существующих, то есть средняя энергия колебаний с ростом температуры растёт.

Температура Дебая — физическая константа вещества, характеризующая многие свойства твёрдых тел — теплоёмкость, электропроводность, теплопроводность, уширение линий рентгеновских спектров, упругие свойства и т. п. Введена впервые П. Дебаем в его теории теплоёмкости.

Температура Дебая определяется следующей формулой:

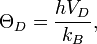
где 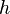— постоянная Планка, 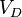— максимальная частота колебаний атомов твёрдого тела, 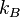— постоянная Больцмана.

Температура Дебая приближённо указывает температурную границу, ниже которой начинают сказываться квантовые эффекты.

А вот со спектром у меня никак отношения не складываются. НО. Вроде там чем больше температура, тем больше спектр колебаний. Естессно до температуры Дебая, там, как сказано выше, амплитуда увеличивается только.

3) Температурная зависимость теплоёмкости по Эйнштейну и по Дебаю

Тут будет много формул, лично я пробежался только по теории. Кратко - эйнштейн был не совсем прав, дебай правильнее сформулировал.

Недостатки теории

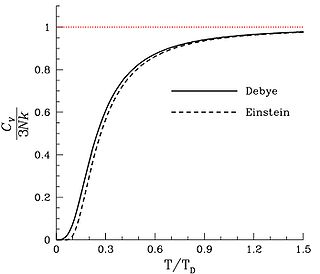
Расхождение теорий Эйнштейна и Дебая

Теория Эйнштейна, однако, недостаточно хорошо согласуется с результатами экспериментов в силу неточности некоторых предположений Эйнштейна, в частности, предположения о равенстве частот колебаний всех осцилляторов. Более точная теория была создана Дебаем в 1912 году.

Модель Дебая

В термодинамике и физике твёрдого тела модель Дебая — метод, развитый Дебаем в 1912 г. для оценки фононного вклада в теплоёмкость твёрдых тел. Модель Дебая рассматривает колебания кристаллической решётки как газ квазичастиц — фононов. Эта модель правильно предсказывает теплоёмкость при низких температурах, которая, согласно закону Дебая, пропорциональна 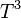. В пределе высоких температур теплоёмкость стремится к 3R, согласно закону Дюлонга — Пти.

При тепловом равновесии энергия E набора осцилляторов с различными частотами 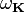равна сумме их энергий:

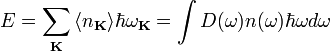
где 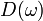— число мод нормальных колебаний на единицу длины интервала частот, 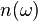— количество осцилляторов в твёрдом теле, колеблющихся с частотой ω.

Функция плотности 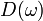в трёхмерном случае имеет вид:

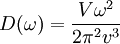
где V — объём твёрдого тела, 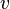— скорость звука в нём.

Значение квантовых чисел вычисляются по формуле Планка:

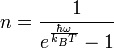
Тогда энергия запишется в виде

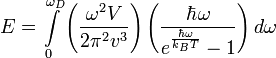
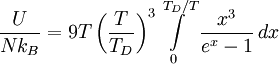
где 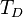— температура Дебая, 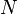— число атомов в твёрдом теле, 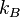— постоянная Больцмана.

Дифференцируя внутреннюю энергию по температуре получим:

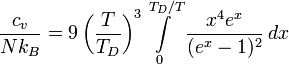
4) Механизм действия Фононов на электропроводность

СМ Лабу 2, теоретическую часть. Кратко :

В диэлектриках теплопроводность пропорциональна произведению теплоемкости фононного газа, скорости фононов и длины их свободного пробега (определяется так называемым рассеянием различного рода).

В металлах теплопроводность определяется в меньшей степени переносом тепловой энергии фононами и в большей степени движением и взаимодействием свободных носителей заряда – электронов проводимости.

5) термическое расширение твердых тел

Диамагнетики

Это вещества, атомы, ионы или молекулы которых не имеют результирующего магнитного момента при отсутствии внешнего поля. Диамагнитный эффект является результатом воздействия внешнего магнитного поля на молекулярные токи и проявляется в том, что возникает магнитный момент, направленный в сторону, обратную внешнему полю. Таким образом, во внешнем магнитном поле диамагнетики намагничиваются противоположно приложенному полю, т. е. имеют отрицательную магнитную восприимчивость (λ < 0). Диамагнитные вещества выталкиваются из неравномерного магнитного поля, а в равномерном магнитном поле вектор намагниченности диамагнетика стремится расположиться перпендикулярно к направлению поля. Диамагнетизм присущ всем без исключения веществам в твердом, жидком и газообразном состояниях, но проявляется слабо и часто подавляется другими эффектами.

Парамагнетики

Это вещества, атомы, ионы или молекулы которых имеют результирующий магнитный момент при отсутствии внешнего магнитного поля. Во внешнем магнитном поле парамагнетики намагничиваются согласно с внешним полем, т. е. имеют положительную магнитную восприимчивость (λ > 0). Парамагнитный эффект присущ веществам с нескомпенсированным магнитным моментом атомов при отсутствии у них порядка в ориентации этих моментов. Поэтому, когда нет внешнего магнитного поля, атомные магнитные моменты располагаются хаотически и намагниченность парамагнитного вещества равна нулю. При воздействии внешнего магнитного поля атомные магнитные моменты получают преимущественную ориентацию в направлении этого поля, и у парамагнитного вещества проявляется намагниченность.

Ферромагнетики

Это вещества, в которых магнитные моменты атомов или ионов находятся в состоянии самопроизвольного магнитного упорядочения, причем результирующие магнитные моменты каждого из доменов отличны от нуля. При воздействии внешнего магнитного поля магнитные моменты доменов приобретают преимущественное ориентирование в направлении этого поля и ферромагнитное вещество намагничивается. Ферромагнитные вещества характеризуются большим значением магнитной восприимчивости (>> 1), а также ее нелинейной зависимостью от напряженности магнитного поля и температуры, способностью намагничиваться до насыщения при обычных температурах даже в слабых магнитных полях, гистерезисом — зависимостью магнитных свойств от предшествующего магнитного состояния, точкой Кюри, т. е. температурой, выше которой материал теряет ферромагнитные свойства. К ферромагнитным веществам относятся железо, никель, кобальт, их соединения и сплавы, а также некоторые сплавы марганца, серебра, алюминия. Ферромагнитные свойства у вещества могут возникать лишь при достаточно большом значении обменного взаимодействия, что характерно для кристаллов железа, кобальта, никеля и др. Необходимое значение обменного взаимодействия ферромагнетики имеют лишь в твердом состоянии. Этим объясняется отсутствие в природе жидких и газообразных ферромагнетиков. Ферромагнетизм сплавов, целиком состоящих из «парамагнитных» компонентов, объясняется тем, что в этих сплавах, основой которых обычно является марганец или хром, введение в решетку основы атомов висмута, сурьмы, серы и теллура изменяет электронную структуру кристаллов, в результате чего создаются условия для возникновения ферромагнетизма.

Антиферромагнетики

Это вещества, в которых магнитные моменты атомов или ионов находятся в состоянии самопроизвольного магнитного упорядочения, причем результирующие магнитные моменты каждого из доменов равны нулю. При воздействии внешнего магнитного поля магнитные моменты атомов приобретают преимущественную ориентацию вдоль внешнего поля и антиферромагнитное вещество намагничивается. Антиферромагнитные вещества характеризуются кристаллическим строением, небольшим коэффициентом магнитной восприимчивости (λ = от 10^-3 до 10^-5), постоянством восприимчивости в слабых полях и сложной зависимостью от магнитного поля в сильных полях, специфической зависимостью от температуры, а также температурой точки Нееля, выше которой вещество переходит в парамагнитное состояние. К антиферромагнетикам относятся чистые металлы хром и марганец, редкоземельные металлы цериевой подгруппы: церий, неодим, празеодим самарий и европий. Редкоземельные металлы диспрозий, гольмий и эрбий в зависимости от температуры могут быть антиферромагнетиками или ферромагнетиками. При воздействии на эти металлы, находящиеся в антиферромагнитном состоянии внешнего магнитного поля, превышающего критическое значение, происходит переход антиферромагнитного порядка в ферромагнитный, сопровождающийся скачкообразным появлением намагниченности (М~ 1600 кА/м). Аналогичные превращения можно наблюдать у тулия и тербия.

Ферримагнетики

Это кристаллические вещества, магнитную структуру которых можно представить в виде двух или более подрешеток; магнитные моменты атомов или ионов находятся в состоянии самопроизвольного магнитного упорядочения, причем результирующие магнитные моменты каждого из доменов отличны от нуля.
Магнитные материалы первой группы применяются в электронных элементах, для которых нет особых требований к температурной и временной нестабильности. Определяющими параметрами данной группы материалов являются начальная магнитная проницаемость и тангенс угла магнитных потерь.
Материалы второй группы имеют малые значения относительного температурного коэффициента магнитной проницаемости в рабочем интервале температур и достаточно высокую временную стабильность начальной магнитной проницаемости. Значение магнитной индукции при поле Н = 800 А/м при нормальной (комнатной) температуре составляет 0,25-0,38 Тл.
К третьей группе относятся материалы с высоким значением начальной магнитной проницаемости на низких частотах. При этом повышенные требования к температурному коэффициенту проницаемости не предъявляются.
Для ферритовых материалов четвертой группы характерны малые значения магнитных потерь в сильных электромагнитных полях и высокое значение магнитной индукции при повышенной температуре (до 100-120°С) и подмагничивании.
Пятая группа ферритов характеризуется повышенными значениями импульсной магнитной проницаемости и температурной стабильностью магнитной проницаемости.
К шестой группе относятся ферритовые материалы, которые характеризуются начальной магнитной проницаемостью, коэффициентом амплитудной нестабильности магнитной проницаемости, коэффициентом перестройки по частоте, тангенсом угла магнитных потерь при различных индукциях, низкой начальной проницаемостью.
Особое место занимают ферритовые материалы седьмой группы. Они характеризуются повышенной добротностью как в слабых, так и в сильных электромагнитных полях, малыми линейными искажениями, низкой начальной проницаемостью.

2) Основные свойства Диамагнетиков и Парамагнетиков.

3) Диамагнетизм и Парамагнетизм.

Оба этих вопроса мы учил из того, что я написал 1 пунктов в части 4 и из Лабы №3. Привожу её ниже.

К слабомагнитным веществам относят диамагнетики и парамагнетики.

Диамагнетизм наблюдается у таких веществ, атомы которых в отсутствие внешнего магнитного поля не обладают магнитными моментами. В этом случае орбитальные и спиновые магнитные моменты электронов в атомах взаимно скомпенсированы. Под воздействием внешнего магнитного поля изменяется орбитальное движение электронов, и каждый из них приобретает индуцированный магнитный момент, направленный против внешнего магнитного поля. При этом магнитная восприимчивость χ = J/B = J/μ₀H (где J – намагниченность вещества, B – магнитная индукция; H – напряженность внешнего магнитного поля, μ₀ – магнитная постоянная) будет отрицательной. Диамагнетизмом обладают все вещества, однако во многих случаях проявление диамагнетизма маскируется более сильными магнитными эффектами (парамагнетизмом, ферромагнетизмом и т. д.)

Парамагнетизм - свойство веществ (парамагнетиков) намагничиваться в направлении внешнего магнитного поля. Он, как правило, проявляется у тех веществ, атомы которых имеют магнитный момент в отсутствие внешнего магнитного поля. Этот магнитный момент обусловлен нескомпенсированными спиновыми магнитными моментами неспаренных электронов атомов. В отсутствие внешнего магнитного поля магнитные моменты атомов ориентированы беспорядочным образом вследствие теплового разбрасывания, а при воздействии внешнего магнитного поля магнитные моменты ориентируются преимущественно вдоль его направления, в результате чего вещество намагничивается. В этом и заключается проявление парамагнетизма. Поскольку увеличение внешнего магнитного поля и нагревание действуют на намагниченность парамагнетика противоположным образом, то при увеличении внешнего магнитного поля и постоянной температуре степень ориентации магнитных моментов и, соответственно, намагниченность возрастают, а при увеличении температуры и постоянном внешнем магнитном поле они, наоборот, уменьшаются.

Магнитная восприимчивость парамагнетиков больше нуля, поскольку вектор намагниченности направлен в том же направлении, что и вектор внешнего магнитного поля. При этом по абсолютной величине она больше магнитной восприимчивости, обусловленной диамагнетизмом, и, следовательно, парамагнитный эффект маскирует диамагнитный эффект. При сравнительно слабых внешних магнитных полях и постоянной температуре магнитная восприимчивость парамагнетиков является постоянной величиной и не зависит от величины внешнего магнитного поля. В сильных магнитных полях имеет место явление насыщения намагниченности, т.е. она приближается к постоянной величине, и магнитная восприимчивость уменьшается с ростом напряженности внешнего магнитного поля.

При сравнительно высоких температурах имеет место

линейная зависимость 1/χ от абсолютной температуры Т:

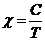, (1)

где С – постоянная Кюри, определяемая природой парамагнетика (величиной магнитного момента атомов).

Это так называемый закон Кюри, который при низких температурах не выполняется даже для обычных парамагнетиков (насыщение намагниченности парамагнетика с уменьшением температуры).

Следует заметить, что сказанное выше относится к обычным парамагнетикам, атомы (ионы, молекулы) которых обладают собственным магнитным моментом. Имеются и другие причины проявления веществом парамагнетизма. Так, в некоторых металлах, например щелочных, парамагнетизм обусловлен не магнитными моментами атомов, а спиновыми магнитными моментами свободных электронов (электронного газа). В таких металлах отсутствует зависимость магнитной восприимчивости от температуры в широких пределах, и закон Кюри не выполняется.

Закон Кюри — физический закон, описывает магнитную восприимчивость парамагнетиков, которая при постоянной температуре для этого вида материалов приблизительно прямо пропорциональна приложенному магнитному полю. Закон Кюри постулирует, что при изменении температуры и постоянном внешнем поле, степень намагниченности парамагнетиков обратно пропорциональна температуре:

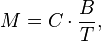
4) Ферромагнетики, их свойства. Кривая технического намагничивания и петля гистерезиса.

СМ Лабу №4, так же то, что писал в пункте 1, 4-ой части.

про Кривую технического намагничивания - Кривая намагничивания, выхо­дящая из начала координат, называется основной кривой. С увеличением поля намагниченность растет сначала медленно, а потом начинается резкий рост: в сравни­тельно узком интервале полей намагниченность увели­чивается в десятки раз. Затем рост намагниченности снова замедляется и наступает так называемое техниче­ское насыщение. Намагничивание до технического насы­щения называется техническим намагничиванием, а соот­ветствующий участок кривой — технической кривой намагничивания ; в нашем случае, как я понял, из Лабы - кривая ОА).

Далее цитирую Лабу №4

В ферромагнетиках вследствие сил обменного взаимодействия, обусловленных специфическим строением электронной оболочки атомов, образуются области спонтанного намагничивания, называемые доменами, в которых магнитные моменты атомов расположены параллельно. При этом магнитные моменты атомов разных доменов направлены разным образом и компенсируют друг друга, так что образец ферромагнетика в целом обладает нулевой намагниченностью. Однако в зависимости от предыстории образца магнитные моменты атомов в разных доменах могут не компенсировать полностью друг друга, и в этом случае образец будет обладать остаточной намагниченностью, т. е. будет являться постоянным магнитом.

Помимо возможности обладания остаточной намагниченностью, характерной особенностью ферромагнетиков является нелинейная зависимость магнитной проницаемости от напряженности магнитного поля. Таким образом, ферромагнетики не обладают постоянной величиной магнитной проницаемости, и можно говорить лишь об их эффективной магнитной проницаемости. При этом ферромагнетики являются сильномагнитными веществами, и их магнитная восприимчивость на несколько порядков больше, чем у слабомагнитных веществ (парамагнетиков и диамагнетиков).

Кроме того, ферромагнетики обладают магнитным гистерезисом, который обусловлен отставанием изменений в структуре ферромагнетика (смещения границ доменов и поворачивания магнитных моментов атомов) от изменения напряженности магнитного поля и представляет собой зависимость намагниченности (или магнитной индукции) ферромагнетика от его предшествующего состояния. Такая зависимость намагниченности (или магнитной индукции) при циклическом изменении напряженности магнитного поля имеет вид петли, называемой петлей гистерезиса (рис. 1).

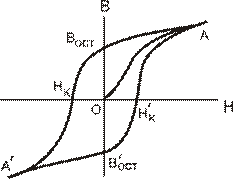
Рис. 1. Петля гистерезиса при перемагничивании ферромагнетика.

Кривую ОА на рис. 1 называют кривой начального намагничивания (От себя - или кривой Технического намагничивания, если я правильно разобрался). Она характеризует намагничивание ферромагнетика, первоначально не обладавшего намагниченностью, и определяется изменениями в доменной структуре, происходящими при увеличении напряженности магнитного поля.

Если после намагничивания ферромагнетика уменьшить напряженность магнитного поля до нуля, в образце ферромагнетика сохраняется остаточная намагниченность В_ост. При дальнейшем увеличении напряженности магнитного поля противоположной направленности намагниченность становится равной нулю. Это происходит при величине напряженности магнитного поля противоположного знака, равной Н_К. Эта величина называется коэрцитивной или задерживающей силой. По величине коэрцитивной силы условно различают мягкие (Н_К<100 А/м) и жесткие (Н_К>100 А/м) ферромагнетики.

При напряженности переменного магнитного поля, обеспечивающей состояние насыщения ферромагнетика, получают максимальную петлю гистерезиса, а при меньших величинах напряженности – частные петли гистерезиса, которых имеется бесконечное множество и все они находятся внутри максимальной петли гистерезиса. При этом концы частных петель находятся на кривой начального намагничивания, что позволяет построить такую кривую и вычислить, например, зависимость магнитной проницаемости μ или магнитной восприимчивости χ от напряженности магнитного поля Н.

Вследствие гистерезиса перемагничивание ферромагнетиков сопровождается выделением тепла. Такое тепло называют теплом гистерезиса. Оно представляет собой работу 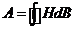, затраченную на перемагничивание единичного объема ферромагнетика за один полный цикл, которая равна площади петли гистерезиса S_loop в координатах B-H:

При нагревании ферромагнетиков изменяются их магнитные характеристики (предельная намагниченность, магнитная проницаемость μ, магнитная восприимчивость χ и т.д.). При некоторой температуре (для каждого ферромагнетика своей) ферромагнетик утрачивает свои специфические свойства и становится парамагнетиком. Эта температура называется ферромагнитной температурой Кюри Θ_К . При этой температуре в ферромагнетике происходит фазовый переход (второго рода). При более высоких температурах Т магнитная восприимчивость χ магнетика (ставшего парамагнетиком) характеризуется линейной зависимостью 1/χ от Т:

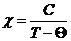, (1)

где Θ – парамагнитная температура Кюри, С – постоянная Кюри.

Эта зависимость получила название закона Кюри-Вейсса. Парамагнитная температура Кюри, определяемая из линейной зависимости 1/χ от Т, находится несколько выше ферромагнитной температуры Кюри Θ_К , однако довольно близко к ней.

Вот и ВСЁ. Что мог, то сделал.

Приближение почти свободных электронов. Модель Кронига–Пенни

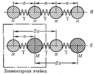
В модели почти свободных электронов, которую предложили Крониг и Пенни, рассматривается движение электрона в линейной цепочке прямоугольных потенциальных ям. Ширина ям равна a, и они отдельны друг от друга потенциальными барьерами толщиной b и высотой 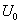. Длина цепочки равна L, а период цепочки равен .

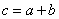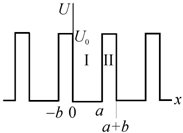Рис. 9.7. Зависимость потенциальной энергии электрона от межатомного расстояния в модели Кронига–Пенни

Пусть E – энергия электрона. Состояние электрона описывается уравнением Шредингера:

.

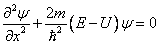(9.26)

Решение этого уравнение разбивается на две части:

1. Для области I (рис. 9.7), где потенциальная энергия 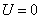, волновая функция, являющаяся решением уравнения (9.26), может быть представлена в виде

.

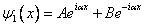(9.27)

Первое слагаемое в уравнении (9.27) соответствует прямой волне, а второе – волне, отраженной от потенциального барьера.

2. Для области II (рис. 9.7), где 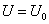, волновую функцию можно записать в виде

.

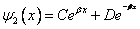(9.28)

В уравнениях (9.27) и (9.28) коэффициенты 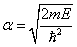, 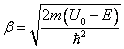; величины A, B, C, D - некоторые константы.

Подставим вместо и 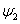одномерную функцию Блоха 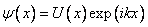и найдем вид периодической функции 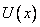в областях I и II:

, .

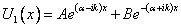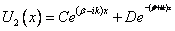(9.29)

Для того чтобы определить коэффициенты A, B, C, D, используем тот факт, что функция 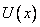и ее первая производная непрерывны в местах скачка потенциала. Например, в точке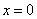

, .

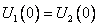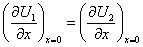Кроме того, функции 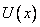обладают свойством периодичности с периодом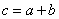

, .

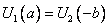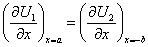Подставляя эти условия в систему уравнений (9.29) для потенциалов 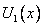и 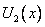, получим четыре уравнения. Известно, что такая система уравнений будет иметь ненулевые решения при условии, что определитель, составленный из коэффициентов при A, B,C, D