По медицинской и биологической физике

ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «КУРСКИЙ ГОСУДАРСТВЕННЫЙ МЕДИЦИНСКИЙ УНИВЕРСИТЕТ» МИНИСТЕРСТВА ЗДРАВООХРАНЕНИЯ И СОЦИАЛЬНОГО РАЗВИТИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Самостоятельная работа №2

По медицинской и биологической физике

«Лазеры и их применение в медицине.

Физические основы интроскопии»

Выполнила: студентка 1 курса 19 группы

лечебного факультета Затей А. О.

Проверил: ст. преп. к.т.н. Чистяков М. В.

Курск 2012 г.

Введение.

Лазеры прочно вошли в нашу жизнь. Невозможно уже, кажется, отыскать отрасль промышленности, производства, где не использовался бы лазер. Особенно – в медицине. Лазер в наше время может значительно облегчить процессы диагностики и лечения различных заболеваний. Приборы, основанные на его применении, активно внедряются в нашу жизнь.

Поэтому нет ничего удивительного в том, что в наше время работникам в сфере здравоохранения просто необходимо знать принципы работы лазера, его устройство, чтобы грамотно применять это средство в профессиональной деятельности. Поэтому ниже мы рассмотрим подробно лазеры, их применение в медицине, а также не обойдем стороной и физические основы интроскопии.

Активная среда

В настоящее время в качестве рабочей среды лазера используются различные агрегатные состояния вещества: твёрдое, жидкое, газообразное, плазма. В обычном состоянии число атомов, находящихся на возбуждённых энергетических уровнях, определяется распределением Больцмана:

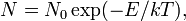
здесь N — число атомов, находящихся в возбуждённом состоянии с энергией E, N0 — число атомов, находящихся в основном состоянии, k — постоянная Больцмана, T — температура среды. Иными словами, таких атомов, находящихся в возбужденном состоянии меньше, чем в основном, поэтому вероятность того, что фотон, распространяясь по среде, вызовет вынужденное излучение также мала по сравнению с вероятностью его поглощения. Поэтому электромагнитная волна, проходя по веществу, расходует свою энергию на возбуждение атомов. Интенсивность излучения при этом падает по закону Бугера[1]:

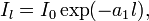
здесь I0 — начальная интенсивность, Il — интенсивность излучения, прошедшего расстояние l в веществе, a1 — коэффициент поглощения вещества. Поскольку зависимость экспоненциальная, излучение очень быстро поглощается.

В том случае, когда число возбуждённых атомов больше, чем невозбуждённых (то есть в состоянии инверсии населённостей), ситуация прямо противоположна. Акты вынужденного излучения преобладают над поглощением, и излучение усиливается по закону[1]:

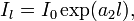
где a2 — коэффициент квантового усиления. В реальных лазерах усиление происходит до тех пор, пока величина поступающей за счёт вынужденного излучения энергии не станет равной величине энергии, теряемой в резонаторе. Эти потери связаны с насыщением метастабильного уровня рабочего вещества, после чего энергия накачки идёт только на его разогрев, а также с наличием множества других факторов (рассеяние на неоднородностях среды, поглощение примесями, неидеальность отражающих зеркал, полезное и нежелательное излучение в окружающую среду и пр.).

Система накачки

Для создания инверсной населённости среды лазера используются различные механизмы. В твердотельных лазерах она осуществляется за счёт облучения мощными газоразрядными лампами-вспышками, сфокусированным солнечным излучением (так называемая оптическая накачка) и излучением других лазеров (в частности, полупроводниковых). При этом возможна работа только в импульсном режиме, поскольку требуются очень большие плотности энергии накачки, вызывающие при длительном воздействии сильный разогрев и разрушение стержня рабочего вещества. В газовых и жидкостных лазерах используется накачка электрическим разрядом. Такие лазеры работают в непрерывном режиме. Накачка химических лазеров происходит посредством протекания в их активной среде химических реакций. При этом инверсия населённостей возникает либо непосредственно у продуктов реакции, либо у специально введённых примесей с подходящей структурой энергетических уровней. Накачка полупроводниковых лазеров происходит под действием сильного прямого тока через p-n переход, а также пучком электронов. Существуют и другие методы накачки (газодинамические, заключающиеся в резком охлаждении предварительно нагретых газов; фотодиссоциация, частный случай химической накачки и др.).

Классическая трёхуровневая система накачки рабочей среды используется, например, в рубиновом лазере. Рубин представляет собой кристалл корунда Al2O3, легированный небольшим количеством ионов хрома Cr3+, которые и являются источником лазерного излучения. Из-за влияния электрического поля кристаллической решётки корунда внешний энергетический уровень хрома E2 расщеплён. Именно это делает возможным использование немонохроматического излучения в качестве накачки. При этом атом переходит из основного состояния с энергией E0 в возбуждённое с энергией около E2. В этом состоянии атом может находиться сравнительно недолго (порядка 10−8 с), почти сразу происходит безызлучательный переход на уровень E1, на котором атом может находиться значительно дольше (до 10−3 с), это так называемый метастабильный уровень. Возникает возможность осуществления индуцированного излучения под воздействием других случайных фотонов. Как только атомов, находящихся в метастабильном состоянии становится больше, чем в основном, начинается процесс генерации.

Следует отметить, что создать инверсию населённостей атомов хрома Cr с помощью накачки непосредственно с уровня E0 на уровень E1 нельзя. Это связано с тем, что если поглощение и вынужденное излучение происходят между двумя уровнями, то оба эти процесса протекают с одинаковой скоростью. Поэтому в данном случае накачка может лишь уравнять населённости двух уровней, чего недостаточно для возникновения генерации.

В некоторых лазерах, например в неодимовом, генерация излучения в котором происходит на ионах неодима Nd3+, используется четырёхуровневая схема накачки. Здесь между метастабильным E2 и основным уровнем E0 имеется промежуточный — рабочий уровень E1. Вынужденное излучение происходит при переходе атома между уровнями E2 и E1. Преимущество этой схемы заключается в том, что в данном случае легко выполнить условие инверсной населенности, так как время жизни верхнего рабочего уровня (E2) на несколько порядков больше времени жизни нижнего уровня (E1). Это значительно снижает требования к источнику накачки. Кроме того, подобная схема позволяет создавать мощные лазеры, работающие в непрерывном режиме, что очень важно для некоторых применений. Однако подобные лазеры обладают существенным недостатком в виде низкого квантового КПД, которое определяется как отношение энергии излученного фотона к энергии поглощенного фотона накачки (ηквантовое = hν_{излучения}/hν_{накачки})

Оптический резонатор

Зеркала лазера не только обеспечивают существование положительной обратной связи, но и работают как резонатор, поддерживая одни генерируемые лазером моды, соответствующие стоячим волнам данного резонатора, и подавляя другие. Если на оптической длине L резонатора укладывается целое число полуволн n:

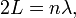
то такие волны, проходя по резонатору не меняют своей фазы и вследствие интерференции усиливают друг друга. Все остальные, близко расположенные волны, постепенно гасят друг друга. Таким образом спектр собственных частот оптического резонатора определяется соотношением:

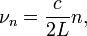
здесь c — скорость света в вакууме. Интервалы между соседними частотами резонатора одинаковы и равны:

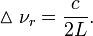
Линии в спектре излучения в силу различных причин (доплеровское уширение, внешние электрические и магнитное поля, квантовомеханическое эффекты и др.) всегда имеют определённую ширину. Поэтому могут возникать ситуации, когда на ширину спектральной линии укладывается несколько собственных частот резонатора. В этом случае излучение лазера будет многомодовым. Синхронизация этих мод позволяет добиться того, чтобы излучение представляло собой последовательность коротких и мощных импульсов. Если же, то в излучении лазера будет присутствовать только одна частота, в данном случае резонансные свойства системы зеркал слабо выражены на фоне резонансных свойств спектральной линии.

При более строгом расчёте необходимо учитывать, что усиливаются волны, распространяющиеся не только параллельно оптической оси резонатора, но и под малым углом к ней. Условие усиления тогда принимает вид:

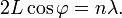
Это приводит к тому, что интенсивность пучка лучей лазера различна в разных точках плоскости, перпендикулярной этому пучку. Здесь наблюдается система светлых пятен, разделённых тёмными узловыми линиями. Для устранения этих нежелательных эффектов используют различные диафрагмы, рассеивающие нити, а также применяют различные схемы оптических резонаторов.

Заряд

Число протонов в ядре определяет непосредственно его электрический заряд, у изотопов одинаковое количество протонов, но разное количество нейтронов. Ядерные свойства изотопов элемента в отличие от химических, могут различаться чрезвычайно резко.

Впервые заряды атомных ядер определил Генри Мозли в 1913 году. Свои экспериментальные наблюдения учёный интерпретировал зависимостью длины волны рентгеновского излучения от некоторой константы, изменяющейся на единицу от элемента к элементу и равной единице для водорода.

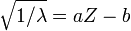
Из чего Мозли сделал вывод, что найденная в его опытах константа атома, определяющая длину волны характеристического рентгеновского излучения и совпадающая с порядковым номером элемента, может быть только зарядом атомного ядра, что стало известно под названием закон Мозли.

Масса

Из-за разницы в числе нейтронов изотопы элемента имеют разную массу 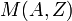, которая является важной характеристикой ядра. В ядерной физике массу ядер принято измерять в атомных единицах массы (а. е. м.), за одну а. е. м. принимают 1/12 часть массы нуклида 12C. Следует отметить, что стандартная масса, которая обычно приводится для нуклида — это масса нейтрального атома. Для определения массы ядра нужно из массы атома вычесть сумму масс всех электронов (более точное значение получится, если учесть еще и энергию связи электронов с ядром).

Кроме того, в ядерной физике часто используется энергетический эквивалент массы. Согласно соотношению Эйнштейна, каждому значению массы соответствует полная энергия:

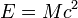
, где — скорость света в вакууме.

Соотношение между а. е. м. и её энергетическим эквивалентом в джоулях:

, а так как 1 электронвольт = 1,602176·10−19 Дж, то энергетический эквивалент а. е. м. в МэВ равен:

.

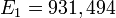Радиус

Анализ распада тяжёлых ядер уточнил оценку Резерфорда и связал радиус ядра с массовым числом простым соотношением:

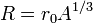
, где r₀ — константа.

Так как радиус ядра не является чисто геометрической характеристикой и связан прежде всего с радиусом действия ядерных сил, то значение зависит от процесса, при анализе которого получено значение , усреднённое значение м, таким образом радиус ядра в метрах:

.

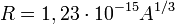Моменты ядра

Как и составляющие его нуклоны, ядро имеет собственные моменты.

Спин

Поскольку нуклоны обладают собственным механическим моментом, или спином, равным, то и ядра должны иметь механические моменты. Кроме того, нуклоны участвуют в ядре в орбитальном движении, которое также характеризуется определённым моментом количества движения каждого нуклона. Орбитальные моменты принимают только целочисленные значения (постоянная Дирака). Все механические моменты нуклонов, как спины, так и орбитальные, суммируются алгебраически и составляют спин ядра.

Несмотря на то, что число нуклонов в ядре может быть очень велико, спины ядер обычно невелики и составляют не более нескольких , что объясняется особенностью взаимодействия одноимённых нуклонов. Все парные протоны и нейтроны взаимодействуют только так, что их спины взаимно компенсируются, то есть пары всегда взаимодействуют с антипараллельными спинами. Суммарный орбитальный момент пары также всегда равен нулю. В результате ядра, состоящие из чётного числа протонов и чётного числа нейтронов, не имеют механического момента. Отличные от нуля спины существуют только у ядер, имеющих в своём составе непарные нуклоны, спин такого нуклона суммируется с его же орбитальным моментом и имеет какое-либо полуцелое значение: 1/2, 3/2, 5/2. Ядра нечётно-нечётного состава имеют целочисленные спины: 1, 2, 3 и т. д.

Магнитный момент

Измерения спинов стали возможными благодаря наличию непосредственно связанных с ними магнитных моментов. Они измеряются в магнетонах и у различных ядер равны от −2 до +5 ядерных магнетонов. Из-за относительно большой массы нуклонов магнитные моменты ядер очень малы по сравнению с магнитными моментами электронов, поэтому их измерение гораздо сложнее. Как и спины, магнитные моменты измеряются спектроскопическими методами, наиболее точным является метод ядерного магнитного резонанса.

Магнитный момент чётно-чётных пар, как и спин, равен нулю. Магнитные моменты ядер с непарными нуклонами образуются собственными моментами этих нуклонов и моментом, связанным с орбитальным движением непарного протона.

Энергия связи

Зависимость средней энергии связи (по оси y) от массового числа (по оси x) ядер.

Большая энергия связи нуклонов, входящих в ядро, говорит о существовании ядерных сил, поскольку известные гравитационные силы слишком малы, чтобы преодолеть взаимное электростатическое отталкивание протонов в ядре. Связь нуклонов осуществляется чрезвычайно короткоживущими силами, которые возникают вследствие непрерывного обмена частицами, называемыми пи-мезонами, между нуклонами в ядре.

Экспериментально было обнаружено, что для всех стабильных ядер масса ядра меньше суммы масс составляющих его нуклонов, взятых по отдельности. Эта разница называется дефектом массы или избытком массы и определяется соотношением:

.

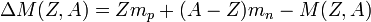Согласно принципу эквивалентности массы и энергии дефект массы представляет собой массу, эквивалентную работе, затраченной ядерными силами, чтобы собрать все нуклоны вместе при образовании ядра. Эта величина равна изменению потенциальной энергии нуклонов в результате их объединения в ядро.

Энергия, эквивалентная дефекту массы, называется энергией связи ядра и равна:

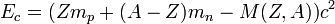
, где — скорость света в вакууме.

Другим важным параметром ядра является энергия связи, приходящаяся на один нуклон ядра, которую можно вычислить, разделив энергию связи ядра на число содержащихся в нём нуклонов:

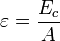
Эта величина представляет собой среднюю энергию, которую нужно затратить, чтобы удалить один нуклон из ядра, или среднее изменение энергии связи ядра, когда свободный протон или нейтрон поглощается в нём.

Как видно из поясняющего рисунка, при малых значениях массовых чисел удельная энергия связи ядер резко возрастает и достигает максимума при 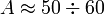(примерно 8,8 Мэв). Нуклиды с такими массовыми числами наиболее устойчивы. С дальнейшим ростом A средняя энергия связи уменьшается, однако в широком интервале массовых чисел значение энергии почти постоянно ( МэВ), из чего следует, что можно записать .

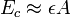Такой характер поведения средней энергии связи указывает на свойство ядерных сил достигать насыщения, то есть на возможность взаимодействия нуклона только с малым числом «партнёров». Если бы ядерные силы не обладали свойством насыщения, то в пределах радиуса действия ядерных сил каждый нуклон взаимодействовал бы с каждым из остальных и энергия взаимодействия была бы пропорциональна , а средняя энергия связи одного нуклона не была бы постоянной у разных ядер, а возрастала бы с ростом .

Общая закономерность зависимости энергии связи от массового числа описывается формулой Вайцзеккера в рамках теории капельной модели ядра.

Устойчивость ядер

Из факта убывания средней энергии связи для нуклидов с массовыми числами больше или меньше 50-60 следует, что для ядер с малыми энергетически выгоден процесс слияния — термоядерный синтез, приводящий к увеличению массового числа, а для ядер с большими — процесс деления. В настоящее время оба этих процесса, приводящих к выделению энергии, осуществлены, причём последний лежит в основе современной ядерной энергетики, а первый находится в стадии разработки.

Детальные исследования показали, что устойчивость ядер также существенно зависит от параметра — отношения чисел нейтронов и протонов. В среднем для наиболее стабильных ядер, поэтому ядра лёгких нуклидов наиболее устойчивы при , а с ростом массового числа всё более заметным становится электростатическое отталкивание между протонами, и область устойчивости сдвигается в сторону (см. поясняющий рисунок).

Если рассмотреть таблицу стабильных нуклидов, встречающихся в природе, можно обратить внимание на их распределение по чётным и нечётным значениям и . Все ядра с чётными значениями этих величин являются ядрами лёгких нуклидов , , , . Среди изобар с нечётными A, как правило, стабилен лишь один. В случае же чётных часто встречаются по два, три и более стабильных изобар, следовательно, наиболее стабильны чётно-чётные, наименее — нечётно-нечётные. Это явления свидетельствует о том, что как нейтроны, так и протоны, проявляют тенденцию группироваться парами с антипараллельными спинами, что приводит к нарушению плавности вышеописанной зависимости энергии связи от A.

Таким образом, чётность числа протонов или нейтронов создаёт некоторый запас устойчивости, который приводит к возможности существования нескольких стабильных нуклидов, различающихся соответственно по числу нейтронов для изотопов и по числу протонов для изотонов. Также чётность числа нейтронов в составе тяжёлых ядер определяет их способность делиться под воздействием нейтронов.

Ядерные силы

Ядерные силы — это силы, удерживающие нуклоны в ядре, представляющие собой большие силы притяжения, действующие только на малых расстояниях. Они обладают свойствами насыщения, в связи с чем ядерным силам приписывается обменный характер (с помощью пи-мезонов). Ядерные силы зависят от спина, не зависят от электрического заряда и не являются центральными силами.

Ядерные реакции

Ядерная реакция — процесс превращения атомных ядер, происходящий при их взаимодействии с элементарными частицами, гамма-квантами и друг с другом.

Радиоактивность

Лишь небольшая часть нуклидов являются стабильными. В большинстве случаев ядерные силы оказываются неспособны обеспечить их постоянную целостность, и ядра рано или поздно распадаются. Это явление получило название радиоактивности.

Ядерный магнитный резонанс

Ядерный магнитный резонанс (ЯМР) — резонансное поглощение или излучение электромагнитной энергии веществом, содержащим ядра с ненулевым спином во внешнем магнитном поле, на частоте ν (называемой частотой ЯМР), обусловленное переориентацией магнитных моментов ядер.

Явление ядерного магнитного резонанса было открыто в 1938 году Исааком Раби в молекулярных пучках, за что он был удостоен нобелевской премии 1944 года. В 1946 году Феликс Блох и Эдвард Миллз Парселл получили ядерный магнитный резонанс в жидкостях и твердых телах (нобелевская премия 1952 года).

Одни и те же ядра атомов в различных окружениях в молекуле показывают различные сигналы ЯМР. Отличие такого сигнала ЯМР от сигнала стандартного вещества позволяет определить так называемый химический сдвиг, который обусловлен химическим строением изучаемого вещества. В методиках ЯМР есть много возможностей определять химическое строение веществ, конформации молекул, эффекты взаимного влияния, внутримолекулярные превращения.

ЯМР интроскопия

Явление ядерного магнитного резонанса можно применять не только в физике и химии, но и в медицине: организм человека — это совокупность все тех же органических и неорганических молекул.

Чтобы наблюдать это явление, объект помещают в постоянное магнитное поле и подвергают действию радиочастотных и градиентных магнитных полей. В катушке индуктивности, окружающей исследуемый объект, возникает переменная электродвижущая сила (ЭДС), амплитудно-частотный спектр которой и переходные во времени характеристики несут информацию о пространственной плотности резонирующих атомных ядер, а также о других параметрах, специфических только для ядерного магнитного резонанса. Компьютерная обработка этой информации формирует объёмное изображение, которое характеризует плотность химически эквивалентных ядер, времена релаксации ядерного магнитного резонанса, распределение скоростей потока жидкости, диффузию молекул и биохимические процессы обмена веществ в живых тканях.

Сущность ЯМР-интроскопии (или магнитно-резонансной томографии) состоит, по сути дела, в реализации особого рода количественного анализа по амплитуде сигнала ядерного магнитного резонанса. В обычной ЯМР-спектроскопии стремятся реализовать, по возможности, наилучшее разрешение спектральных линий. Для этого магнитные системы регулируются таким образом, чтобы в пределах образца создать как можно лучшую однородность поля. В методах ЯМР-интроскопии, напротив, магнитное поле создается заведомо неоднородным. Тогда есть основание ожидать, что частота ядерного магнитного резонанса в каждой точке образца имеет свое собственное значение, отличающееся от значений в других частях. Задав какой-либо код для градаций амплитуды ЯМР-сигналов (яркость или цвет на экране монитора), можно получить условное изображение (томограмму) срезов внутренней структуры объекта.

ЯМР-интроскопия, ЯМР-томография впервые в мире изобретены в 1960 г. В. А. Ивановым. Заявку на изобретение (способ и устройство) некомпетентный эксперт отклонил «… ввиду явной бесполезности предлагаемого решения», поэтому авторское свидетельство на это было выдано лишь более чем через 10 лет. Таким образом, официально признано, что автором ЯМР-томографии является российский учёный. Невзирая на этот юридический факт, Нобелевская премия была присуждена за ЯМР-томографию вовсе не В. А. Иванову.

ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «КУРСКИЙ ГОСУДАРСТВЕННЫЙ МЕДИЦИНСКИЙ УНИВЕРСИТЕТ» МИНИСТЕРСТВА ЗДРАВООХРАНЕНИЯ И СОЦИАЛЬНОГО РАЗВИТИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Самостоятельная работа №2

по медицинской и биологической физике

«Лазеры и их применение в медицине.