Задачи расчета магнитных полей

Рассмотрим некоторые типы задач расчета магнитных полей.

Первый тип задач - определение индуктивности какого-либо контура или взаимной индуктивности двух контуров.

Второй тип задач - определение сил, действующих в магнитном поле на движущийся электрон, неподвижный проводник с током, ферромагнитные массы в магнитном поле.

Третий тип задач - расчет поля, создаваемого заданным распределением токов в пространстве.

Четвертый тип задач - расчет магнитных экранов. Магнитными экранами называют устройства, предназначенные для ослабления магнитного поля в заданной области пространства по сравнению с магнитным полем вне экрана. К магнитной экранировке прибегают, например, для защиты чувствительных приборов от влияния посторонних магнитных полей, в частности от влияния магнитного поля Земли.

Пятый тип задач - нахождение распределения токов в некотором объеме для получения заданной картины магнитного поля. Так, например, в морском деле большое значение имеет дегауссировка кораблей: корабль, обладая большой ферромагнитной массой, возмущает магнитное поле Земли не только в непосредственной близости от себя, но и на достаточно большом расстоянии. Соответствующие индикаторы на возмущение магнитного поля Земли могут привести в действие находящиеся поблизости самодвижущиеся мины (имеются в виду условия военного времени), и в результате корабль может оказаться подорванным. Чтобы этого не случилось, на кораблях устанавливают специальные намагничивающие обмотки, которые располагают таким образом, чтобы скомпенсировать возмущение магнитного поля Земли вблизи корабля.

Много различных задач на расчет магнитных полей возникает при магнитной записи звука, а также при магнитной дефектоскопии. Магнитная дефектоскопия позволяет по картине магнитного поля судить о наличии раковин, трещин и других дефектов в изделиях из ферромагнитных материалов. Широко распространена она на железнодорожном транспорте при контроле целостности рельсов железнодорожного пути. Широкое распространение ее объясняется экономичностью и быстротой осуществления контроля.

Общая характеристика методов расчета и исследования магнитных полей

Методы расчета и исследования магнитных полей можно подразделить на три группы: аналитическую, графическую и экспериментальную.

Группа аналитических методов объединяет все чисто аналитического порядка приемы интегрирования уравнения Пуассона (для областей, занятых током), уравнения Лапласа (для областей, не занятых током), применение методов зеркальных и конформных отображений и др.

В силу трудностей математического характера классические аналитические методы позволяют решать относительно небольшой круг задач. В тех случаях, когда расчет поля аналитическими методами вызывает затруднения, прибегают к графическому методу построения картины поля или к исследованию магнитного поля на модели. Графические методы построения картины поля применимы к двухмерным безвихревым полям. За последние годы был развит метод интегральных уравнений, предполагающий использование ЭВМ и значительно расширяющий круг решаемых задач.

Пояснения к решению задач

Магнитное поле характеризуется векторной величиной В, называемой магнитной индукцией. Магнитная индукция В измеряется в В·с/м².

Интеграл вектора магнитной индукции по некоторой поверхности называется магнитным потоком через эту поверхность

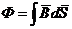. (1)

Магнитный поток измеряется в системе СИ в веберах (Вб).

Магнитное поле не имеет дивергенции, поскольку 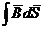= 0. По теореме Гаусса

,

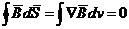следовательно,

divB = ÑB = 0.

Величина магнитной индукции в данной точке от тока в проводнике определяется интегралом

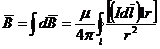, (2)

причем интегрирование ведется по всему замкнутому контуру тока, состоящему из элементов Idl.

Из векторного анализа известно, что векторная величина, не имеющая дивергенции, сама является ротором другой векторной величины. Следовательно, вектор магнитной индукции В является ротором другого вектора А, получившего название векторного потенциала магнитного поля

B = rotA = [ÑA]. (3)

Векторный потенциал А измеряется в В·с/м.

Значение векторного потенциала А выводится из (2). Поскольку 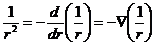векторное произведение .

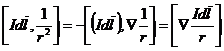Такое преобразование сделать можно, так как оператор является символом дифференцирования по координатам точки наблюдения, то есть по r, тогда как вектор Idl для Ñ является величиной постоянной. Теперь

.

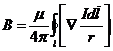Так как интегрирование ведется по l и вектор 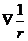для интеграла является постоянной величиной, можно сделать такую перестановку

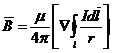. (4)

Сравнивая (3) и (4), можно написать

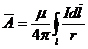. (5)

Подставляя вместо элемента тока Idl = dSdl = ddv, где d—плотность тока, dv—элемент объема проводника, по­лучим

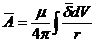. (6)

По аналогии с электрическим полем, для которого справедливо уравнение Пуассона, 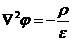, где 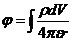для векторного потенциала А можно напиcать

ѲA = -md (7)

или ѲA = 0, если в рассматриваемом объеме отсутствует электрический ток.

Используя известное соотношение в векторном анализе, можно написать

ѲA = Ñ(ÑA) – [Ñ[ÑA] = - md.

Из (6) видно, что поле вектора А, такое же как и поле вектора d, поэтому по аналогии с последним div A = ÑA = 0. Следовательно,

[Ñ[ÑA]] = md

или

[ÑB] = m [ÑH] = md

и

[ÑH] = d, (8)

что принято называть первым уравнением Максвелла. Подставив в (1) значение В из (3), будем иметь

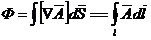. (9)

Индуктивность L контура есть величина магнитного потока, сцепленного с данным контуром тока, приходящегося на единицу тока. Разделив (9) на I, получим

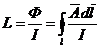. (10)

Индуктивность L измеряется в Ом*с = Гн (генри).

Взаимная энергия W контура с током и постороннего магнитного поля равна IФ. Подставив значения Ф из (9), будем иметь значение взаимной энергии двух контуров с токами 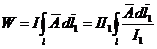, где I₁ ток в контуре l₁. Деление подинтегрального выражения на I₁ с одновременным умножением интеграла на I₁ ничего не изменит, поскольку сила тока I₁ контура l₁ при интегрировании является величиной постоянной.

Величина 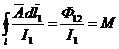, равная потоку контура l₁ при токе в 1 А, пронизывающему контур с током I, называется взаимной индуктивностью двух контуров с токами I и I₁.

Примеры решениЯ задач

Задача 1. Над стальной поверхностью на расстоянии h от нее протянут тонкий длинный провод (рис.1), по которому протекает электрический ток I. Найти напряженность магнитного поля в стали в точках, расположенных на расстоянии от поверхности стали 0,5h, 1,0h, 1,5h, и построить картину магнитного поля в ней, если m₁ =9m₀.

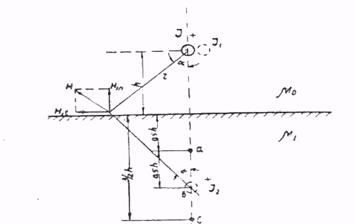Рис.1.

Решение.Подобные задачи проще решать по методу зеркальных изображений. Магнитное поле в воздухе рассматривается как сумма полей от действительного тока I в воздухе и его зеркального изображения I₂, причем I₂ имеет одинаковое направление с I, но отличается по величине. Магнитное доле в стали рассматривается как сумма полей от действительного тока I и тока I₁, причем токи I и I₁ разные по величине и направлению, протекающие по одному и тому же проводу.

Используя граничные условия магнитного поля Н_1t =Н_2t, B_1n = B_2n и выразив значения Н_1t, Н_2t, В_1n и В_2n через действительный ток I и его изображения, а, именно,

, ,

, ,

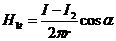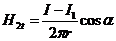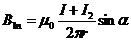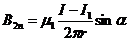после решения уравнений, получим

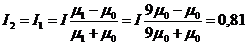
Напряженность поля в точке а

;

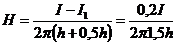в точке b: ;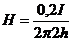

в точке с: .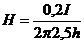

Так как в области стали магнитное поле определяется токами I и I₁, протекающими по одному проводу, то линии магнитных сил будут окружностями с центром, совпадающими с осью действительного провода.

Задача 2.Найти значение векторного потенциала для магнитного поля внутри и вне бесконечно длинного цилиндрического провода радиуса а (рис. 2). Материал провода—медь. По проводу протекает постоянный ток с плотностью d.

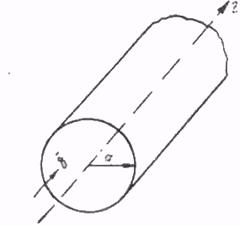Рис. 2.

Решение.Будем исходить из уравнения Пуассона. Так как векторный потенциал имеет в данной задаче одну компоненту вдоль оси z и зависит только от z, исходное уравнение Пуассона в цилиндрических координатах запишется так:

;

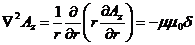для меди m = 1.

Ввиду того, что вектор плотности тока 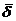направлен по оси z, вектор потенциал имеет только одну составляющую А_z. Интегрируем это уравнение

,

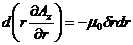откуда .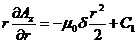

Беря повторный интеграл, находим .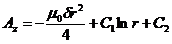

Вне цилиндра d = 0, и, следовательно, А_z = С₃lnr + С₄,

где С₃ и С₄ новые постоянные (учитывая различие в граничных условиях внутри и вне провода).

Для определения постоянных интегрирования найдем значение магнитной индукции. В области внутри провода

.

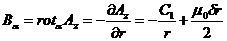В области вне провода ,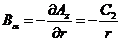

(остальные компоненты ротора тождественно равны нулю).

Определим постоянные C₁ и С₂ для области внутри провода. Так как В должно остаться всюду конечным, то C₁ = 0; примем, что при x = 0 векторный потенциал A = 0, тогда получим, что С₃ = 0. Следовательно, А_z = .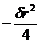

В области вне провода постоянные C₃ и C₄ определяются из условия непрерывности векторного потенциала на границе r = а

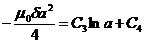
и непрерывности тангенциальной составляющей вектора Н, что при m=const означает непрерывность тангенциальной составляющей вектора В. Из двух последних уравнений определяем

; ,

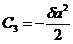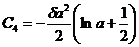что позволяет написать значение А_z

.

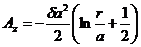Основные формулы

Закон полного тока

.

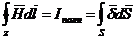Закон Био-Савара:

.

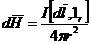Закон Ампера:

dF = I[dl,B] .

Зависимость между магнитной индукцией и напряженностью магнитного поля (изотропные среды):

B = m_aH = mm₀H = m₀H + J ,

m₀ = 4·10^-7 Гн/м – магнитная постоянная; m - относительная магнитная проницаемость; m_а – абсолютная магнитная проницаемость.

Интенсивность намагничивания:

J = m₀c_мH,

где c_м – относительная магнитная восприимчивость.

Первое уравнение Максвелла для постоянных токов:

rotH = d = gE; div m_aH = 0.

Зависимость между напряженностью магнитного поля и векторным потенциалом:

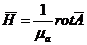; div A = 0 .

Вектор магнитного поля:

.

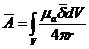Основные уравнения магнитного поля:

rot A = B = m_aH; ѲA = - m_ad .

Граничные условия в магнитном поле:

B_1n – B_2n = 0; H_1t – H_2t = s,

где σ = 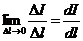- поверхностная плотность тока.

Энергия магнитного поля:

.

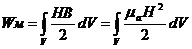Магнитный поток: .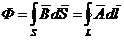

Соленоидальность магнитного поля:

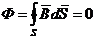, или .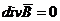

Векторный потенциал линейного тока: .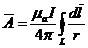

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какое поле называется потенциальным полем?

2. Можно ли магнитное поле рассматривать, как потенциальное, то есть определять напряженность поля Н как градиент некоторого скаляра?

3. Как определяется напряженность магнитного поля из векторного магнитного потенциала?

4. Каково физическое значение векторного потенциала?

5. Что такое закон полного потока?

6. Какие величины магнитного поля аналогичны в формально-математическом отношении электростатическому полю и полю постоянного тока?

7. В чем состоит сущность метода зеркальных изображений при расчете магнитных полей?