Магнитное поле постоянного тока

Глава тринадцатая

МАГНИТНОЕ ПОЛЕ ПОСТОЯННОГО ТОКА

Интегральная форма закона полного тока

Количественная связь между циркуляцией вектора Нпо замкнутому контуру и током внутри контура определяется законом полного тока в интегральной форме — линейный интеграл от напряженности магнитного поля вдоль любого замкнутого контура равен полному току, пронизывающему замкнутый контур:

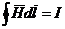. (13.3)

Под полным током понимают весь ток (ток проводимости и ток смещения), пронизывающий контур интегрирования.

Интегральную форму закона полного тока применяют, когда может быть использована симметрия в поле. Так, например, напряженность поля в некоторой точке А в поле уединенного прямого провода с током I (рис. 13.2) по закону полного тока определяют следующим образом. Проведем через точку А окружность радиусом R в плоскости, перпендикулярной оси провода, так что центр ее находится на этой оси. В силу симметрии напряженность поля во всех точках окружности численно одна и та же. Направление напряженности совпадает с касательной к окружности. Поэтому

; .

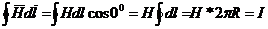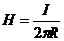С увеличением радиуса R напряженность магнитного поля убывает по гиперболическому закону.

Если какое-либо поле имеет сложный характер и не удается составить замкнутый контур, все точки которого находились бы в симметричных условиях, то хотя интегральная форма записи закона полного тока справедлива и для такого контура, использовать ее для нахождения напряженности в любой точке поля так просто не удается (нельзя вынести из-под знака интеграла).

Запись ротора в виде векторного произведения

Формально rotHможно представить в виде векторного произведения оператора пространственного дифференцирования Ñ на вектор Н, т. е. rotН=[ÑН]. В этом нетрудно убедиться путем непосредственного умножения Ñ на H:

.

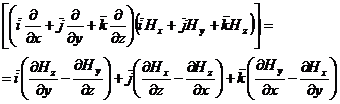Выражение проекций ротора в цилиндрической и сферической системах координат

Без вывода приведем выражение проекций ротора H:

в цилиндрической системе координат:

;

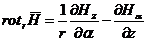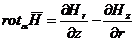; (13.6)

;

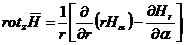в сферической системе координат:

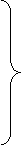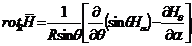
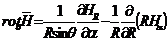(13.7)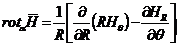

Магнитное поле в областях «занятых» и «не занятых»

Постоянным током

Вихревыми принято называть поля, ротор которых отличен от нуля. Так как для магнитного поля постоянного тока rot H = d, то во всех точках пространства, где d ¹ 0, поле вектора H является вихревым. В областях пространства, где d = 0, rot Н = 0, магнитное поле можно рассматривать как потенциальное.

Граничные условия

Подобно тому, как в электростатическом поле и в поле проводящей среды выполнялись определенные граничные условия, в магнитном поле также имеют место аналогичные условия:

Н_1t =Н_2t, (13.12)

В_1n =В_2n (13.13)

Условие (13.12) означает, что на границе раздела двух однородных и изотропных сред, различных в магнитном отношении (различные m), равны тангенциальные составляющие векторов напряженности магнитного поля. Условие (13.13) свидетельствует о равенстве нормальных составляющих векторов магнитных индукций на границе раздела. Условие (13.12) выводят путем составления линейного интеграла 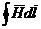по плоскому контуру mnpq (рис. 13.5, б) и приравнивания его нулю (так как он не охватывает тока). Стороны nр и qm ничтожно малы по сравнению со сторонами mn и pq. Длину стороны mn и равную ей по величине длину стороны pq обозначим через dl. Тогда H₁sina₁dl — Н₂sina₂dl = 0, но H₁sina₁ = Н_1t, H₂sina₂ = Н_2t, следовательно Н_1t = Н_2t.

Условие (13.12) не выполняется, если на поверхности раздела двух сред протекает так называемый поверхностный ток. Под ним понимают ток, протекающий по бесконечно тонкому плоскому проводнику, помещенному на границе раздела. В этом случае 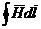будет равняться не нулю, а поверхностному току sdl, который оказался внутри замкнутого контура:

H₁sina₁dl — Н₂sina₂dl = sdl и в силу этого H_1t — Н_2t = s.

Другими словами, при наличии поверхностного тока с плотностью s тангенциальная составляющая напряженности поля терпит разрыв. Как правило, поверхностный ток отсутствует, и условие (13.12) выполняется. Равенство нормальных составляющих векторов магнитной индукции следует из принципа непрерывности магнитного потока:

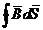= 0.

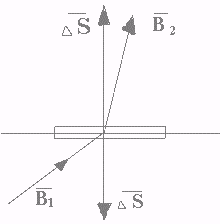
Для того чтобы убедиться в справедливости (13.13), на границе раздела выделим небольшой плоский параллелепипед и подсчитаем потоки вектора Вчерез нижнюю грань (рис. 13.6) —B_1nDS и верхнюю B_2nDS. Сумма потоков равна нулю: —В_1nDS + B_2nDS = 0. Следовательно, B_1n = B_2n.

Из (13.12) и (13.13) вытекает соотношение

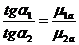. (13.14)

Рис.13.6. Граничные условия на границе раздела двух тел с различными магнитными проницаемостями.

Оно дает связь между углом падения a₁ и углом преломления a₂ (рис. 13.5, б). Если магнитные силовые линии выходят из среды с большой магнитной проницаемостью, например m_1a = 10⁴ m₀, в среду с малой магнитной проницаемостью, например в воздух m_2a = m₀, то

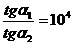и tga₁ = 10^-4 tga₂.

Следовательно, угол a₂ много меньше угла a₁.

Например. Найти угол a₂, под которым силовые линии выходят в среду с магнитной проницаемостью m_2a, если угол a₁ = 89°;

m_1a = 10⁴ m₀, m_2a = m₀.

Решение. tga₁ = tg 89°= 57,29;

tga₂ = 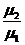tga₁ = 10^-4 tga₁ = 0,005729; a₂ = 20'.

Пояснения к решению задач

Магнитное поле характеризуется векторной величиной В, называемой магнитной индукцией. Магнитная индукция В измеряется в В·с/м².

Интеграл вектора магнитной индукции по некоторой поверхности называется магнитным потоком через эту поверхность

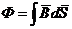. (1)

Магнитный поток измеряется в системе СИ в веберах (Вб).

Магнитное поле не имеет дивергенции, поскольку 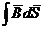= 0. По теореме Гаусса

,

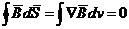следовательно,

divB = ÑB = 0.

Величина магнитной индукции в данной точке от тока в проводнике определяется интегралом

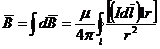, (2)

причем интегрирование ведется по всему замкнутому контуру тока, состоящему из элементов Idl.

Из векторного анализа известно, что векторная величина, не имеющая дивергенции, сама является ротором другой векторной величины. Следовательно, вектор магнитной индукции В является ротором другого вектора А, получившего название векторного потенциала магнитного поля

B = rotA = [ÑA]. (3)

Векторный потенциал А измеряется в В·с/м.

Значение векторного потенциала А выводится из (2). Поскольку 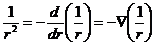векторное произведение .

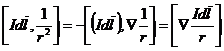Такое преобразование сделать можно, так как оператор является символом дифференцирования по координатам точки наблюдения, то есть по r, тогда как вектор Idl для Ñ является величиной постоянной. Теперь

.

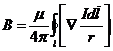Так как интегрирование ведется по l и вектор 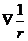для интеграла является постоянной величиной, можно сделать такую перестановку

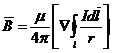. (4)

Сравнивая (3) и (4), можно написать

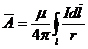. (5)

Подставляя вместо элемента тока Idl = dSdl = ddv, где d—плотность тока, dv—элемент объема проводника, по­лучим

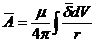. (6)

По аналогии с электрическим полем, для которого справедливо уравнение Пуассона, 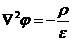, где 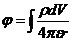для векторного потенциала А можно напиcать

ѲA = -md (7)

или ѲA = 0, если в рассматриваемом объеме отсутствует электрический ток.

Используя известное соотношение в векторном анализе, можно написать

ѲA = Ñ(ÑA) – [Ñ[ÑA] = - md.

Из (6) видно, что поле вектора А, такое же как и поле вектора d, поэтому по аналогии с последним div A = ÑA = 0. Следовательно,

[Ñ[ÑA]] = md

или

[ÑB] = m [ÑH] = md

и

[ÑH] = d, (8)

что принято называть первым уравнением Максвелла. Подставив в (1) значение В из (3), будем иметь

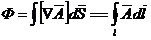. (9)

Индуктивность L контура есть величина магнитного потока, сцепленного с данным контуром тока, приходящегося на единицу тока. Разделив (9) на I, получим

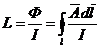. (10)

Индуктивность L измеряется в Ом*с = Гн (генри).

Взаимная энергия W контура с током и постороннего магнитного поля равна IФ. Подставив значения Ф из (9), будем иметь значение взаимной энергии двух контуров с токами 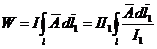, где I₁ ток в контуре l₁. Деление подинтегрального выражения на I₁ с одновременным умножением интеграла на I₁ ничего не изменит, поскольку сила тока I₁ контура l₁ при интегрировании является величиной постоянной.

Величина 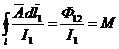, равная потоку контура l₁ при токе в 1 А, пронизывающему контур с током I, называется взаимной индуктивностью двух контуров с токами I и I₁.

Примеры решениЯ задач

Задача 1. Над стальной поверхностью на расстоянии h от нее протянут тонкий длинный провод (рис.1), по которому протекает электрический ток I. Найти напряженность магнитного поля в стали в точках, расположенных на расстоянии от поверхности стали 0,5h, 1,0h, 1,5h, и построить картину магнитного поля в ней, если m₁ =9m₀.

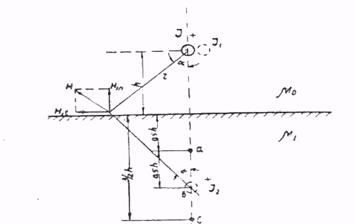Рис.1.

Решение.Подобные задачи проще решать по методу зеркальных изображений. Магнитное поле в воздухе рассматривается как сумма полей от действительного тока I в воздухе и его зеркального изображения I₂, причем I₂ имеет одинаковое направление с I, но отличается по величине. Магнитное доле в стали рассматривается как сумма полей от действительного тока I и тока I₁, причем токи I и I₁ разные по величине и направлению, протекающие по одному и тому же проводу.

Используя граничные условия магнитного поля Н_1t =Н_2t, B_1n = B_2n и выразив значения Н_1t, Н_2t, В_1n и В_2n через действительный ток I и его изображения, а, именно,

, ,

, ,

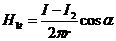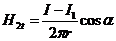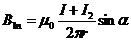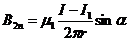после решения уравнений, получим

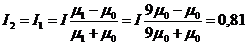
Напряженность поля в точке а

;

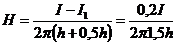в точке b: ;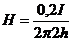

в точке с: .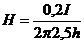

Так как в области стали магнитное поле определяется токами I и I₁, протекающими по одному проводу, то линии магнитных сил будут окружностями с центром, совпадающими с осью действительного провода.

Задача 2.Найти значение векторного потенциала для магнитного поля внутри и вне бесконечно длинного цилиндрического провода радиуса а (рис. 2). Материал провода—медь. По проводу протекает постоянный ток с плотностью d.

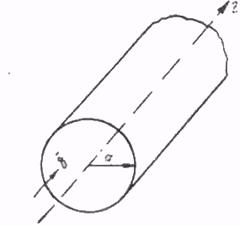Рис. 2.

Решение.Будем исходить из уравнения Пуассона. Так как векторный потенциал имеет в данной задаче одну компоненту вдоль оси z и зависит только от z, исходное уравнение Пуассона в цилиндрических координатах запишется так:

;

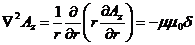для меди m = 1.

Ввиду того, что вектор плотности тока 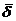направлен по оси z, вектор потенциал имеет только одну составляющую А_z. Интегрируем это уравнение

,

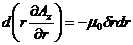откуда .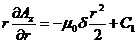

Беря повторный интеграл, находим .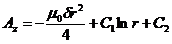

Вне цилиндра d = 0, и, следовательно, А_z = С₃lnr + С₄,

где С₃ и С₄ новые постоянные (учитывая различие в граничных условиях внутри и вне провода).

Для определения постоянных интегрирования найдем значение магнитной индукции. В области внутри провода

.

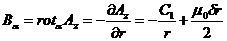В области вне провода ,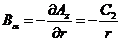

(остальные компоненты ротора тождественно равны нулю).

Определим постоянные C₁ и С₂ для области внутри провода. Так как В должно остаться всюду конечным, то C₁ = 0; примем, что при x = 0 векторный потенциал A = 0, тогда получим, что С₃ = 0. Следовательно, А_z = .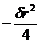

В области вне провода постоянные C₃ и C₄ определяются из условия непрерывности векторного потенциала на границе r = а

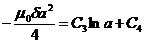
и непрерывности тангенциальной составляющей вектора Н, что при m=const означает непрерывность тангенциальной составляющей вектора В. Из двух последних уравнений определяем

; ,

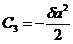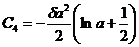что позволяет написать значение А_z

.

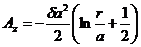Основные формулы

Закон полного тока

.

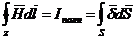Закон Био-Савара:

.

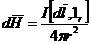Закон Ампера:

dF = I[dl,B] .

Зависимость между магнитной индукцией и напряженностью магнитного поля (изотропные среды):

B = m_aH = mm₀H = m₀H + J ,

m₀ = 4·10^-7 Гн/м – магнитная постоянная; m - относительная магнитная проницаемость; m_а – абсолютная магнитная проницаемость.

Интенсивность намагничивания:

J = m₀c_мH,

где c_м – относительная магнитная восприимчивость.

Первое уравнение Максвелла для постоянных токов:

rotH = d = gE; div m_aH = 0.

Зависимость между напряженностью магнитного поля и векторным потенциалом:

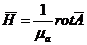; div A = 0 .

Вектор магнитного поля:

.

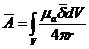Основные уравнения магнитного поля:

rot A = B = m_aH; ѲA = - m_ad .

Граничные условия в магнитном поле:

B_1n – B_2n = 0; H_1t – H_2t = s,

где σ = 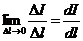- поверхностная плотность тока.

Энергия магнитного поля:

.

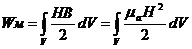Магнитный поток: .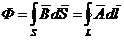

Соленоидальность магнитного поля:

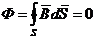, или .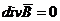

Векторный потенциал линейного тока: .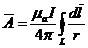

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какое поле называется потенциальным полем?

2. Можно ли магнитное поле рассматривать, как потенциальное, то есть определять напряженность поля Н как градиент некоторого скаляра?

3. Как определяется напряженность магнитного поля из векторного магнитного потенциала?

4. Каково физическое значение векторного потенциала?

5. Что такое закон полного потока?

6. Какие величины магнитного поля аналогичны в формально-математическом отношении электростатическому полю и полю постоянного тока?

7. В чем состоит сущность метода зеркальных изображений при расчете магнитных полей?

Глава тринадцатая

МАГНИТНОЕ ПОЛЕ ПОСТОЯННОГО ТОКА