Круговые процессы. Обратимые и необратимые процессы. Тепловая машина. II начало термодинамики
Круговой процесс (цикл) – это процесс, в результате которого система, пройдя через ряд промежуточных состояний, возвращается в исходное состояние.
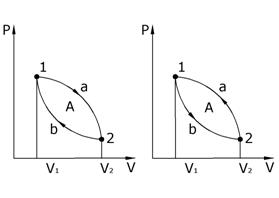 | Любой цикл включает два процесса: расширения газа (участок 1–2, а рис. 6.6, а), в котором работа А12 > 0, и сжатие газа (участок 2–1, b), где работа А21 < 0. Таким образом, работа за цикл определяется как А = А12 – А21. |
| Рис. 6.6 |
Так как система возвращается в исходное состояние, то ее внутренняя энергия остается постоянной. Рис. 6.6, а иллюстрирует прямой цикл, который лежит в основе действия тепловой машины, а 6.6, б – обратный, реализованный в холодильной установке. Схема работы тепловой машины представлена на рис. 6.7.
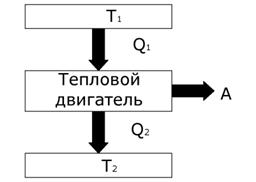 | За цикл рабочее тело получает от нагревателя количество тепла 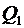 и отдает холодильнику количество теплоты и отдает холодильнику количество теплоты 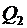 . Полезная работа определяется разностью полученной и отданной теплоты . Полезная работа определяется разностью полученной и отданной теплоты 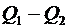 , а коэффициент полезного , а коэффициент полезного |
| Рис. 6.7 |
действия выражается как

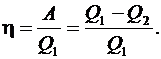 (6.46)
(6.46)
Все циклы, а также тепловые процессы, протекающие в природе, являются необратимыми.
Термодинамический процесс (цикл) называется обратимым, если при совершении его сначала в прямом, а затем в обратном направлениях, как сама система, так и все внешние тела возвращаются в исходное состояние. Если это не выполняется, то процесс необратим.
II начало термодинамики допускает несколько формулировок:
Невозможен вечный двигатель второго рода, т. е. периодически действующий двигатель, совершающий работу за счет охлаждения одного источника теплоты.
Невозможен процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя в эквивалентную ей работу (формулировка Кельвина).
Теплота никогда не может переходить сама собой от тел с более низкой температурой к телам с более высокой температурой (формулировка Клаузиуса).
Цикл Карно и его КПД
Карно рассмотрел работу идеальной тепловой машины, обладающей наибольшим коэффициентом полезного действия  .
.
В основе цикла Карно лежит круговой процесс, представленный на рис. 6.8, состоящий из двух изотерм (1–2 и 3–4) и двух адиабат (2–3 и 4–1). В качестве рабочего тела используется один моль идеального газа, заключенный в сосуд с подвижным поршнем.
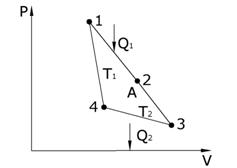 | Работа на участке 1–2 (T = const) количество тепла, полученное газом от нагревателя 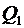 , равно работе расширения газа , равно работе расширения газа 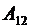 , которая определяется как , которая определяется как |
| Рис. 6.8. |
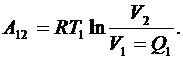 (6.47)
(6.47)
При адиабатическом расширении газа (участок 2–3) работа равна:
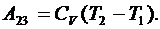 (6.48)
(6.48)
Количество теплоты 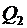 , отданное газом холодильнику, при изотермическом сжатии (участок 2–3), равно работе сжатия А34:
, отданное газом холодильнику, при изотермическом сжатии (участок 2–3), равно работе сжатия А34:
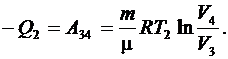 (6.49)
(6.49)
На участке 4–1 работа адиабатического сжатия определяется как
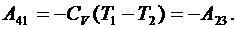 (6.50)
(6.50)
Таким образом, работа за цикл 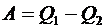 , так как
, так как  и определяется площадью кругового процесса на рис. 6. 8.
и определяется площадью кругового процесса на рис. 6. 8.
Коэффициент полезного действия цикла согласно формуле (6.46) равен
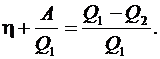 (6.51)
(6.51)
Из уравнений адиабат следует, что
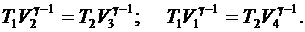
Откуда
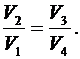 (6.52)
(6.52)
Подставив выражения (6.47) и (6.49) для 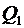 и
и 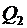 в формулу (6.52), получим
в формулу (6.52), получим
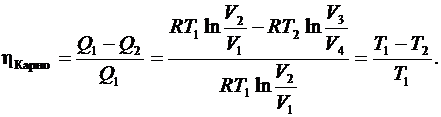 (6.53)
(6.53)
Формула (6.53) была получена Клаузиусом. КПД цикла Карно определяется только температурой нагревателя и холодильника
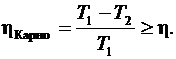 (6.54)
(6.54)
Таким образом, идеальная тепловая машина, работающая по обратимому циклу Карно, имеет наибольший КПД, определяемый температурой нагревателя Т1 и холодильника Т2, не зависящий от конструкции машины.
Энтропия
Понятие энтропии введено Клаузиусом. Коэффициент полезного действия реальной тепловой машины всегда меньше h идеальной машины, т. е.
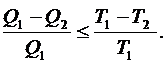 (6.55)
(6.55)
Выражение (6.55) можно записать в следующем виде
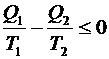 – неравенство Клаузиуса, (6.56)
– неравенство Клаузиуса, (6.56)
где 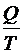 – приведенная теплота; знак «–» учитывает, что на каком-то участке цикла тепло отдается.
– приведенная теплота; знак «–» учитывает, что на каком-то участке цикла тепло отдается.
Из неравенства Клаузиуса следует, что для обратимого цикла алгебраическая сумма приведенной теплоты равна нулю.
Если разбить весь обратимый цикл Карно на бесконечно малые циклы, то для каждого из них можно записать
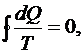 (6.57)
(6.57)
где 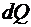 – бесконечно малое количество теплоты, переданное (отнятое) телу при температуре Т.
– бесконечно малое количество теплоты, переданное (отнятое) телу при температуре Т.
Из (6.57) следует, что 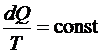 и является функцией состояния, которую Клаузиус назвал энтропией S, что по-гречески означает «превращение», т. е.
и является функцией состояния, которую Клаузиус назвал энтропией S, что по-гречески означает «превращение», т. е.
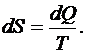 (6.58)
(6.58)
Изменение энтропии не зависит от пути перехода из одного состояния в другое, а определяется состоянием системы.
II начало термодинамики можно сформулировать, используя понятие энтропии. Если в изолированной системе происходят только обратимые процессы, то ее энтропия остается постоянной, т. е.
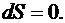 (6.59)
(6.59)
И, наоборот, при необратимых процессах энтропия в изолированной системе возрастает
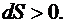 (6.60)
(6.60)
В открытой системе энтропия может как возрастать, так и убывать, или оставаться неизменной.
