Частица находится в потенциальном ящике в основном состоянии. Какова вероятность обнаружения частицы: в средней трети ящика; в крайней трети ящика.

27. Частица находится в бесконечно глубоком одномерном прямоуголь-ном потенциальном ящике. Найти отношение разности ∆Е_n,n+1 соседних энергитических уровней к энергии ∆Е_n частицы в трех случаях :1) n = 2; 2) n = 5; 3) n →∞.

28. Используя соотношение неопределенностей, оценить наименьшие ошибки ∆р в определении импульса электрона и протона, если координаты центра масс этих частиц могут быть установлены с неопределенностью ∆х = 0,01 мм.

29. Время жизни τ возбужденного ядра порядка 1 нс, длина волны излучения равна 0,1 нм. С какой наибольшей точностью (∆ε) может быть определена энергия излучения?

30. Частица находится в бесконечно глубоком одномерном прямо-угольном потенциальном ящике в основном состоянии. Какова вероятность ω обнаружения частицы в крайней четверти ящика?

31. Атом испустил фотон с длиной волны 800 нм. Продолжительность излучения 10 нс. Определить наибольшую точность (∆λ), с которой может быть измерена длина волны излучения.

32. Альфа – частица находится в бесконечно глубоком, одномерном потенциальном прямоугольном ящике. Используя соотношение неопределенностей, оценить ширину ящика, если известно, что минимальная энергия α – частицы 8 МэВ.

33. Электрон находится в бесконечно глубоком одномерном прямоуголь-ном потенциальном ящике шириной L. В каких точках в интервале 0<x<L плотности вероятности нахождения электрона на втором и третьем энергитических уровнях одинаковы? Вычислить плотность вероятности для этих точек. Решение пояснить графиком.

34. Электрон находится в бесконечно глубоком одномерном прямоуголь-ном потенциальном ящике шириной L= 0,1 нм. Определить в электрон – вольтах наименьшую разность энергетических уровней электрона.

35. Частица находится в бесконечно глубоком одномерном прямо-угольном потенциальном ящике шириной L в возбужденном состоянии n = 3. Определить в каких точках интервала 0<x<L плотность вероятности нахождение частицы имеет максимальное и минимальное значения.

Оценить наименьшие ошибки, которыми можно определить скорость электрона, протона и шарика массой 1 мг, если координаты частиц и центра шарика установлены с неопределенностью 1 мкм.

Оценить с помощью соотношения неопределенностей скорости элек-трона в атоме водорода, полагая размер атома 0,1 нм. Сравнить полученную величину со скоростью электрона на первой боровской орбите данного атома.

Оценить с помощью соотношения неопределенностей минимальную возможную энергию электрона в атоме водорода и соответствующее эффективное расстояние его от ядра.

Электрон с кинетической энергией 4 эВ локализован в области размером 1 мкм. Оценить с помощью соотношения неопределенностей относительную неопределенность его скорости.

Оценить с помощью соотношения неопределенностей кинетическую энергию электрона, движущегося в области размер которой 0,1 нм.

41. Электрон движется со скоростью 10⁶ м/с. Допустим, что мы можем измерить его положение с точностью до 10^{-12 м. Сравнить неопределен-ность импульса электрона ∆р с самим значением его импульса р.}

42. Теннисный мяч массой 200 г движется со скоростью 30 м/с. Если мы можем определить положение мяча с ошибкой, соизмеримой с длиной волны света, используемого при наблюдении (например, 500 нм), то как соотносится неопределенность в установлении его импульса с самим импульсом мяча?

43. Оценить неопределенность импульса протона в ядре. Размер ядра 10^{-15 м.}

Радиоактивность.

Основной закон радиоактивного распада:

,

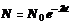
где N – число нераспавшихся атомов в момент времени t; N₀ – число нераспавшихся атомов в момент, принятый за начальный (при t = 0); e – основание натуральных логорифмов; λ – постоянная радиоактивного распада.

Период полураспада Т_½ – промежуток времени, за который число нераспавшихся атомов уменьшается в два раза. Период полураспада связан с постоянной распада соотношением:

Т_½ =

Число атомов, распавшихся за время t

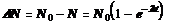
Если промежуток времени ∆t <<Т_½ , то для определения числа рас-павшихся атомов можно применять приближеггую формулу:

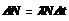
Среднее время жизни τ радиоактивного ядра – промежуток времени, за которой число нераспавшихся ядер уменьшается в е раз:

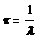
Число атомов, содержащихся в радиоактивном изотопе:

,

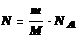
где m – масса изотопа;М – молярная масса; N_A – постоянная Авогадро.

Активность А нуклида в радиоактивном источнике (активность изотопа) если величина, равна отношению числа dN ядер, распав-шихся в изотопе, к промежутку времени dt, за которое произошел распад.

Активность определяется по формуле:

,

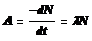
или после замены N по основному закону радиоактивного распада

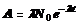
Активность изотопа в начальный момент времени (t = 0)

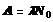
Активность изотопа изменяется со временем по тому же закону, что и число нераспавшихся ядер:

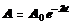
Массовая активность а радиоактивного источника есть величина, рав-ная отношению его активности А к массе m этого источника:

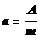
Если имеется смесь ряда радиоактивных изотопов, образующихся один из другого, и если постоянная распада λ, первого члена ряда много меньше постоянных всех остальных членов ряда, то в смеси устанавливается состояние радиоактивного равновесия, при котором активности всех членов ряда равны между собой:

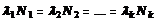
Пример решения задачи.

При определении периода полураспада T_1/2 короткоживущего радиоактивного изотопа использован счетчик импульсов. За время Δt = 1мин в начале наблюдения (t = 0) было насчитано Δn₁ = 250 импульсов, а по истечении t = 1ч за то же время Δt — Δn₂ = 92 импульса. Определить постоянную радиоактивного распада λ и период полураспада T_1/2 изотопа.

Решение. Число импульсов Δn, регистрируемых счетчиком за время Δt, пропорционально числу распавшихся атомов ΔN. Таким обра­зом, при первом измерении

Δn₁=kΔN₁= kN₁(1 – e^-λΔt) (1)

где N₁ — количество радиоактивных атомов к моменту начала отсчета;

к — коэффициент пропорциональности (постоянный для данного при­бора и данного расположения прибора относительно радиоактивного изо­топа).

При повторном измерении (предполагается, что расположение прибо­ров осталось прежним)

Δn₂=kΔN₂= kN₂(1 – e^-λΔt) (2)

где N₂ — количество радиоактивных атомов к моменту начала второго измерения.

Разделив соотношение (1) на выражение (2) и приняв во внимание, что по условию задачи Δt одинаково в обоих случаях, а также, что N₁ и N₂ связаны между собой соотношением N₂= N₁ e^-λt, получим

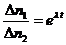
где t — время, прошедшее от первого до второго измерения. Для вы­числения λ выражение следует прологарифмировать: 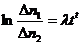, откуда

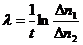
Подставив числовые данные, получим постоянную радиоактивного распада, а затем и период полураспада:

λ = 1 ч^-1; Т_1/2 = 41,5 мин.

Ответ: λ = 1 ч^-1; Т_1/2 = 41,5 мин.

Задачи.

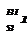1. Определить начальную активность А₀ радиоактивного препарата магния ²⁷Mg массой 0,2 мкг, а так же его активность А через время 6 ч. Период полураспада Т_½ магния считать известным.

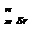2. Определить число N атомов радиоактивного препарата иода массой 0,5 мкг, распавшихся в течении времени: 1) t₁ = 1 м; 2)t₂ = 7 сут.