Н.А. Очкина, С.С. Саранцева, О.А. Захаров

Н.А. Очкина, С.С. Саранцева, О.А. Захаров

ФИЗИЧЕСКАЯ КАРТИНА МИРА

Часть 3. КВАНТОВО-ПОЛЕВАЯ КАРТИНА МИРА

Учебное пособие

Пенза 2012

УДК 535(100)

ББК 22.314

О94

Рецензент –

кандидат технических наук, доцент кафедры «Физики» Тертычная С.В. (ПГУ)

ОчкинаН.А. Физическая картина мира. Ч.3. Квантово-полевая картина мира [Текст]: учеб. пособие / Н.А. Очкина, С.С. Саранцева, О.А. Захаров. Под общей редакцией Г.И. Грейсуха. – Пенза: ПГУАС, 2012. – 85 с.

В учебном пособии рассматривается квантово-полевая картина мира (КПКМ) как этап формирования общих представлений о физической картине мира.

Пособие содержит: формулировку основополагающих гипотез и полное изложение теоретического материала по истории открытия явлений, а также введения новых понятий и тер­минов, лежащих в основе КПКМ; формулировку основных законов и описание осно­вополагающей теории КПКМ – квантовой механики; изложение основных положений и принципов КПКМ. В конце теоретической части пособия приведёны вопросы для самопроверки, которые помогут студентам самостоятельно оценить качество усвоения материала.

В сборник включёны методические указания к лабораторным работам по волновой оптике и квантовой теории электромагнитного излучения, в которых приведены общие методические сведения об изучаемом явлении, описание лабораторной установки, порядок проведения измерений и обработки экспериментальных данных.

Учебное пособие разработано на кафедре физики ПГУАС и предназначено для использования студентами специальностей «Менеджмент» и «Маркетинг», выполняющими лабораторные работы по курсу «Концепции современного естест­вознания».

Настоящее пособие может быть рекомендовано для инженерно-экономических и гума­нитарных специальностей вузов по курсу «Концепции современного естест­вознания».

© Пензенский государственный университет

архитектуры и строительства, 2012

© Очкина Н.А., Саранцева С.С.,

Захаров О.А., 2012

ПРЕДИСЛОВИЕ

Настоящее пособие является третьей частью раздела «Физическая картина мира» по курсу «Концепции современного естествознания» для инженерно-экономических и гуманитарных специальностей уни­верситетов.

В качестве главных взаимосвязанных целей изучения данного раздела приняты следующие:

– формирование представлений о том, что явления микромира принципиально познаваемы;

– понимание того, что основой познания объектов и явлений микромира является эксперимент, представляющий собой непосредственное материальное взаимодействие между средствами исследования субъекта и объектом изучения;

– осознание того, что в микромире причинность (как один из элементов всеобщей связи и взаимообусловленности вещей, явлений и событий материального мира) реализуется через многообразие случайностей, поэтому микропроцессам свойственны не динамические, а статистические закономерности;

– признание объективного существования физического мира, т.е. его существования независимо от человека и его сознания;

– изучение практических результатов развития квантовой физики (микро- и наноэлектроника, лазерные технологии, ядерная и термоядерная энергетика, компьютерная техника и информационные технологии).

Достижение поставленных целей с учетом относительно неболь­шого объёма изучаемого раздела потребовало взвешенного подхода к отбору материала, обеспечения сбалансированного изложения с еди­ных позиций наиболее фундаментальных вопросов естествознания и их прикладных аспектов.

В первой части пособия содержится:

– полное изложение теоретического материала по истории открытия физических явлений, получивших объяснение с помощью квантовых представлений;

– введение новых понятий и терминов;

– описание основополагающей теории КПКМ – квантовой механики;

– изложение основных положений и принципов КПКМ.

Во второй части пособия приведены методические указания к лабораторным работам по волновой оптике и квантовой теории электромагнитного излучения, выполнение которых позволяет студентам глубже освоить теоретический материал, а также приобрести элементарные навыки экспериментирования на совре­мен­ном оборудовании.

В тексте данного учебного пособия наиболее важные положения и термины, а также формулировки законов выделены жирным шрифтом или курсивом. Это способствует более быстрому усвоению материала студентами. Вопросы для самопроверки, поме­щённые в конце глав, помогут студентам самостоятельно оценить качество усвоения материала.

ВВЕДЕНИЕ

Квантово – полевая картина мира (XX в.) формируется на основе:

— квантовой гипотезы немецкого физика Макса Планка (1858-1947гг.);

— волновой механики австрийского физика-теоретика Эрвина Шрёдингера (1887-1961гг.);

— квантовой механики немецкого физика-теоретика Вернера Гейзенберга (1901-1976гг.);

— квантовой теории атома датского физика Нильса Бора (1885-1962гг.).

В рамках КПКМ сложились квантово – полевые представления о материи:

– материя обладает корпускулярными и волновыми свойствами, т. е. каждый элемент материи имеет свойства частицы и волны.

– движение становится лишь частным случаем физического взаимодействия.

– пространство и время – относительны, зависимы от материи и друг от друга, образуя единый четырёхмерный пространственно – временной континуум.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

ИНТЕРФЕРЕНЦИЯ СВЕТА. МЕТОДЫ ПОЛУЧЕНИЯ КОГЕРЕНТНЫХ ПУЧКОВ

Интерференцией(от лат. inter – взаимно и ferio – ударяю)света называется явление пространственного перераспределения энергии светового излучения при наложении двух или нескольких световых волн.

Впервые явление интерференции обнаружили в XVII в. независимо друг от друга английские физики Роберт Бойль (1627-1691 гг.) и Роберт Гук (1635-1703 гг.). Они наблюдали разноцветную окраску тонких плёнок (масляных или бензиновых пятен на поверхности воды).

Открытое ими явление исследовал И. Ньютон, однако он не смог его объяснить с точки зрения своей корпускулярной теории света. Правильное объяснение интерференции света как типично волнового явления было дано только в начале XIX века английским учёным Томасом Юнгом (1773-1829гг.) и французским физиком Огюстеном Френелем (1788-1826гг.).

В 1801 году Юнг, ввёл принцип суперпозиции и объяснил «цветастость» тонких пленок интерференцией лучей, отражённых от внешней и внутренней поверхности плёнки. Толщина плёнки обычно меняется от места к месту, поэтому она окрашивается во все цвета радуги.

Устойчивая во времени интерференционная картина – ряд чередующихся тёмных и светлых полос может наблюдаться только при наложении когерентных волн.

Когерентныминазываются волны с одинаковой частотой, поляризацией и постоянной разностью фаз.

Юнг был первым, кто понял, что волны от двух разделённых в пространстве и независящих друг от друга источников света не когерентны. Поэтому он пропустил в тёмную комнату солнечный свет через узкую щель (шириной около 1 мкм), затем с помощью двух щелей и такой же ширины, находящихся друг от друга на расстоянии порядка нескольких микрон, разделил этот пучок света на два (рис.1.1). Проходя через каждую из щелей, световой пучок уширялся вследствие дифракции, поэтому на белом экране Э световые пучки, прошедшие через щели и , перекрывались. В области перекрытия световых пучков наблюдалась устойчивая интерференционная картина в виде чередующихся светлых и темных полос. В центре экрана видна полоса белого солнечного света. Остальные интерференционные максимумы окрашены.

Рис.1.1. Опыт Юнга

В своём опыте Юнг достаточно точно определил длину световой волны: для крайней фиолетовой части спектра он получил значение длины волны 0,42 мкм, для красного света – 0,7 мкм.

Таким образом, в классическом опыте Юнга когерентные световые пучки были получены путём разделения и последующего сведения лучей, исходящих от общего источника света.

Разделение света на когерентные пучки можно осуществить и другими методами: с помощью зеркал и преломляющих поверхностей (метод зеркал Френеля, метод зеркала Ллойда, метод бипризмы Френеля, метод тонких пленок и др.).

Рассмотрим некоторые из них.

Зеркало Ллойда.

В опыте, предложенном ирландским физиком Хэмфри Ллойдом (1800-1881гг.), источником света служит узкая щель, параллельная плоскости зеркала (рис. 1.2). Расходящийся световой пучок от источника падает на плоское зеркало (зеркало Ллойда), расположенное перпендикулярно к экрану . Отразившись от зеркала, он попадает на экран. Этот пучок света можно представить исходящим от мнимого изображения источника света , образованного зеркалом. Кроме того, на экран попадают лучи, идущие непосредственно от источника света . В той области экрана, где перекрываются оба пучка света, т.е. накладываются две когерентные волны, наблюдается интерференционная картина.

Рис 1.2. Опыт Ллойда

Особенность интерференционной картины, наблюдаемой с помощью зеркала Ллойда, заключается в том, что центральная полоса получается не светлой, а темной. Это указывает на то, что лучи, проходящие одинаковые геометрические пути, все же сходятся в опыте Ллойда с разностью хода . Такая «потеря» полуволны (или, другими словами, изменение фазы на π) происходит при отражении света от поверхности стекла, коэффициент преломления которого больше, чем воздуха.

Зеркала Френеля.

Френель предложил в качестве двух когерентных источников воспользоваться двумя изображениями одного и того же действительного источника света в двух плоских зеркалах и , образующих двугранный угол , отличающийся от 180° всего на несколько угловых минут.

Схема опыта Френеля представлена на рисунке 1.3.

Рис. 1.3. Зеркала Френеля

– расстояние от источника света до места соприкосновения зеркал.

Для построения изображений источника в обоих зеркалах воспользуемся тем, что мнимое изображение, даваемое плоским зеркалом, лежит за зеркалом на таком же расстоянии, на каком источник расположен перед зеркалом. Проведем из точки окружность с радиусом и опустим из точки перпендикуляр на продолжение прямой . Точка пересечения продолжения этого перпендикуляра с окружностью является мнимым изображением источника в первом зеркале . Аналогично строится мнимое изображение источника во втором зеркале .

На экране, где пучки, отражённые от зеркал, перекрываются, наблюдается интерференционная картина в виде равноотстоящих тёмных и светлых полос.

Бипризма Френеля.

Бипризма Френеля состоит из двух стеклянных призм, соединенных боковыми сторонами (рис. 1.4).

– преломляющий угол призмы; 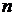– абсолютный показатель преломления материала призмы.

Рис.1.4. Получение когерентных пучков с помощью бипризмы Френеля

Свет от источника преломляется в обеих призмах, в результате чего за призмой распространяются пучки, как бы исходящие от мнимых источников и , разнесённых на расстояние и являющихся когерентными. На экране, расположенном за бипризмой эти пучки интерферируют.

Интерференционную картину, создаваемую когерентными волнами, можно наблюдать визуально, фотографировать, измерять расстояние между светлыми и темными полосами и т.д. Некогерентные лучи не дают стабильной интерференционной картины. Непрерывное изменение фаз складываемых колебаний в каждой точке пространства создает быстро меняющуюся картину, которую невоз­мож­но использовать для измерительных целей.

ЗАКОНОМЕРНОСТИ ИНТЕРФЕРЕНЦИИ

Пусть волны от двух точечных источников света и одинаковой частоты и одинаковой поляризации (в этом случае можно отвлечься от векторного характера электрического поля световой волны) освещают экран

(рис. 1.5).

Рис.1.5. Интерференция света

Определим интенсивность света в точке экрана.

Электрические векторы волн в точке соответственно равны

(1.1)

где и оптические пути, пройденные волнами от источников и до точки в среде с абсолютным показателем преломления волновое число; длина волны в вакууме; и амплитуды напряженностей электромагнитных волн в точке ; и начальные фазы.

Введя обозначения и (1.2)

перепишем уравнения (1.1) в виде

(1.3)

Амплитуду результирующего колебания легко найти с помощью векторной диаграммы, изображенной на рис. 1.6.

Рис. 1.6. Векторная диаграмма для определения амплитуды результирующего колебания

По теореме косинусов

(1.4)

Учитывая, что интенсивности волн, пропорциональны квадратам их амплитуд, выразим интенсивность результирующего колебания по формуле

(1.5)

Так как в реальных некогерентных источниках излучателями являются отдельные атомы, не связанные друг с другом, то разность фаз непрерывно изменяется, принимая с равной вероятностью любые значения, так что среднее по времени значение равно нулю. В этом случае интенсивность волны во всех точках экрана равна сумме интенсивностей складываемых волн

(1.6)

Интенсивность света во всех точках экрана просто равна сумме интенсивностей, что соответствует закону сохранения энергии. Поэтому при сложении некогерентных волн интерференция не возникает.

Если же разность фаз возбуждаемых волнами колебаний равна нулю или остается постоянной во времени, то волны являются когерентными. Источники таких волн также когерентны. В этом случае имеет постоянное во времени, но свое для каждой точки экрана значение, в результате чего в одних местах возникают максимумы интенсивности, а в других – минимумы, т.е. наблюдается интерференционная картина.

Рассмотрим случай сложения когерентных колебаний от двух синфазных источников

При , т.е. при (где целое число 0, 1, 2..., называемое порядком интерференционного максимума), интенсивность результирующего колебания будет максимальна и равна

(1.7)

При т.е. при интенсивность результирующего колебания будет минимальной

(1.8)

Принимая во внимание обозначения (1.2), можно выразить разность фаз по формуле

, (1.9)

где – оптическая разность хода волн.

С учетом формулы (1.9), условия возникновения максимумов и минимумов интенсивности результирующей волны можно записать в виде:

если , (1.10)

если . (1.11)

Интерференционные максимумы наблюдаются в точках пространства, для которых оптическая разность хода интерферирующих волн равна целому числу длин волн.

Интерференционные минимумы наблюдаются в точках пространства, для которых оптическая разность хода интерферирующих волн равна нечётному числу полуволн.

Таким образом, суммарная интенсивность зависит от положения точки наблюдения. На экране будут наблюдаться светлые и тёмные интерференционные полосы. Интенсивность периодически изменяется вдоль оси от до Пространственный период изменения интенсивности называется шириной интерференционной полосы (рис.1.5).

ПРИМЕНЕНИЕ ИНТЕРФЕРЕНЦИИ

Явление интерференции света находит широкое применение в современной технике. Например, интерференция света в тонких плёнках используется для просветления оптики.

Просветление оптики – это уменьшение отражения света от поверхности линзы в результате нанесения на неё специальной плёнки.

Отполированная поверхность стекла отражает примерно 4% падающего на неё света. Современные оптические приборы состоят из большого числа деталей, изготовленных из стекла. Проходя через каждую из этих деталей, свет ослабляется на 4%. Общие потери света в объективе фотоаппарата составляют примерно 25%, в призменном бинокле и микроскопе – 50%.

Для уменьшения световых потерь в оптических приборах все стеклянные детали, через которые проходит свет, покрывают тонкой плёнкой, толщина и показатель преломления которой выбираются с таким расчётом, чтобы в отражённом свете возник интерференционный минимум. В результате в проходящем свете возникает интерференционный максимум, т.е. через линзу пройдёт больше света, чем при отсутствии плёнки. Таким образом, оптика просветляется.

Чаще всего для просветления оптики используют прозрачный материал – с показателем преломления , меньшим, чем показатель преломления стекла ( ).

	При отражении света от границ раздела воздух-плёнка и плёнка-стекло возникает интерференция когерентных лучей 1' и 2' (рис. 1.7). Чтобы эти лучи гасили друг друга, их амплитуды должны быть равны, а в оптической разности хода должна укладываться полуволна . (1.12) С другой стороны, при падении луча перпендикулярно плёнке,
Рис.1.7. Просветляющее покрытие

, (1.13)

где – толщина пленки.

Из уравнений (1.12) и (1.13) следует, что минимальная толщина просветляющей плёнки составляет четверть длины волны

. (1.14)

Интерференция света широко используется при спектральном анализе для точного измерения расстояний и углов.

С помощью интерферометров – приборов, в которых явление интерференции используется для прецизионных (весьма точных измерений), можно измерить коэффициенты линейного расширения твёрдых тел, а также измерить весьма малое изменение размеров ферромагнетиков в магнитном поле или сегнетоэлектриков в электрическом поле (магнитострикционный и электрострикционный эффекты).

С помощью интерференционных методов измеряют коэффициенты преломления веществ, в частности газов; определяют весьма малые концентрации примесей в жидкостях и газах; проверяют качество шлифовки поверхностей. Если на исследуемой поверхности имеется царапина или вмятина, то это приводит к искривлению интерференционных полос. По характеру искривления полос можно судить о глубине царапины.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Из всех видов излучения наиболее распространённым является температурное, или тепловое.

Тепловым излучением называется электромагнитное излучение, возникающее за счет внутренней энергии излучающего тела и зависящее только от температуры и оптических свойств этого тела.

Тепловое излучение свойственно всем телам при температуре выше абсолютного нуля. Оно имеет сплошной спектр, т.е. содержит элект­ро­магнитные волны всех длин от нуля до бесконечности.

Характерная особенность теплового излучения состоит в том, что в адиабатно замкнутой (теплоизолированной) системе устанавливается тепловое равновесие между тепловым излучением и излучающим телом.

Количественной мерой энергии, излучаемой телом в единицу времени, является поток (мощность) излучения 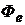, численно равный отношению энергии 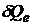, переносимой излучением за малый промежуток времени 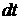, к величине этого промежутка

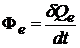. (2.1)

Поток теплового излучения, испускаемый с единицы площади поверхности излучателя в телесный угол 2p во всем интервале длин волн, называется энергетической светимостью тела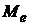

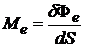. (2.2)

Для характеристики распределения излучения по длинам волн, т.е. для оценки энергетической светимости в единичном спектральном диапазоне, используют спектральную плотность энергетической светимости
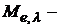физическую величину, численно равную отношению энергетической светимости 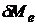в малом спектральном интервале (от 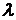до 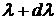) к ширине этого интервала

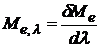. (2.3)

Тогда суммарное излучение тела, т.е. его энергетическую светимость можно рассчитать по формуле

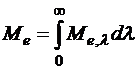(2.4)

При падении на тело поток излучения в общем случае разделяется на три части: одна часть пропускается телом, другая отражается, а третья поглощается и, увеличивая внутреннюю энергию тела, повышает его температуру.

С количественной стороны эти части характеризуются:

Коэффициентом пропускания

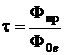, (2.5)

Коэффициентом отражения

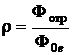(2.6)

и коэффициентом поглощения

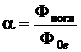, (2.7)

где 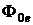– поток (мощность) падающего излучения; Ф_пр – поток прошедшего излучения; Ф_отр – поток отражённого излучения; Ф_погл – поток поглощённого излучения.

Коэффициенты t, r и a зависят от свойств самого тела и длины волны падающего излучения. Спектральная зависимость, т.е. зависимость коэффициентов от длины волны, определяет цвет как прозрачных, так и непрозрачных (t= 0) тел.

Согласно закону сохранения энергии

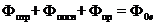. (2.8)

Разделив обе части равенства (2.8) на 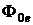, получим:

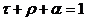(2.9)

Тело, для которого 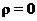, , 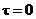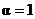называется абсолютно чёрным.

Абсолютно чёрное тело – это тело, которое при любой не разрушающей его температуре полностью поглощает всю энергию падающего на него излучения любой длины волны. Все реальные тела не являются абсолютно чёрными. Однако некоторые из них в определенных интервалах длин волн близки по своим свойствам к абсолютно чёрному телу. Например, в области длин волн видимого света коэффициенты поглощения сажи, платиновой черни и черного бархата мало отличаются от единицы.

Наиболее совершенной моделью абсолютно чёрного тела может служить малое отверстие в замкнутой полости сферической формы. Свет, попадающий через отверстие внутрь полости, будет многократно отражаться от стенок, прежде чем сможет выйти наружу. При каждом отражении свет, независимо от материала стенок, частично поглощается. В результате многократных отражений внутри полости излучение будет практически полностью поглощено, и отверстие снаружи кажется совершенно чёрным. Очевидно, что эта модель тем ближе по характеристикам к чёрному телу, чем больше отношение площади поверхности полости к площади отверстия (рис. 2.1).

Рис. 2.1. Модель абсолютно чёрного тела

Каждое тело может не только испускать, но и поглощать тепловое излучение. Опыты показывают, что чем больше энергии тело излучает при некоторой постоянной температуре, тем сильнее оно поглощает излучение такого же спектрального состава при той же температуре.

Спектральной характеристикой поглощения электромагнитных волн телом является спектральный коэффициент поглощения 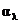– величина, определяемая отношением поглощённого телом потока излучения в малом спектральном интервале (от 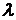до 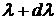) к потоку падающего на него излучения в том же спектральном интервале

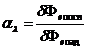. (2.10)

В 1859 г. немецкий физик Густав Кирхгоф (1824-1887гг.) на основании второго начала термодинамики установил один из основных законов теплового излучения.

Закон Кирхгофа: отношение спектральной плотности энергетической светимости равно­весного излучения тела к его спектральному коэффициенту поглощения не зависит от природы тела; для всех тел оно является универсальной функцией длины волны излучения и температуры тела

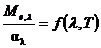. (2.11)

Закон Кирхгофа был подтвержден опытным путём.

Для абсолютно чёрного тела 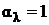. Поэтому из закона Кирхгофа следует, что

,

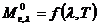где 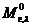– спектральная плотность энергетической светимости абсолютно чёрного тела.

Таким образом, универсальная функция Кирхгофа 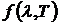представляет собой спектральную плотность энергетической светимости абсолютно чёрного тела. Поэтому выражение закона Кирхгофа (2.11) можно записать в виде

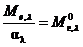. (2.12)

Из формулы (2.12) следует, что:

1) для всех тел отношение спектральной плотности энергетической светимости к спектральному коэффициенту поглощения равно спектральной плотности энергетической светимости абсолютно чёрного тела при тех же значениях 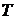и ;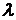

2) спектральная плотность энергетической светимости любого тела в любой области спектра всегда меньше спектральной плотности энергетической светимости абсолютно чёрного тела (при одних и тех же значениях длины волны и температуры);

3) если тело при некоторой температуре не поглощает электромагнитные волны в интервале длин от 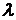до 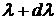, то оно их в этом интервале длин при данной температуре и не излучает;

4) тело, которое при данной температуре сильнее поглощает, должно интенсивнее излучать. Например, при накаливании платиновой пластинки, часть которой покрыта платиновой чернью, её зачернённый конец светится значительно ярче, чем светлый.

Аналитический вид функции 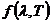для абсолютно черного тела
был установлен учеником Кирхгофа Максом Планком на основе квантовых представлений о природе излучения.

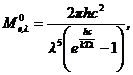(2.13)

где 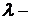длина волны излучения; 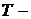температура излучающего тела; 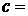3×10⁸ 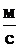– скорость света в вакууме; k = 1,38×10^-23 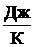– постоянная Больцмана; 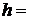6,63×10^-34 Дж×с – постоянная Планка.

Спектр излучения абсолютно черного тела имеет характерный максимум (рис. 2.2), который при повышении температуры сдвигается в коротковолновую часть (рис. 2.3).

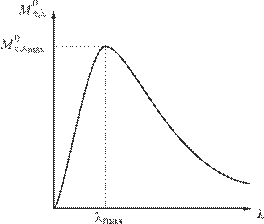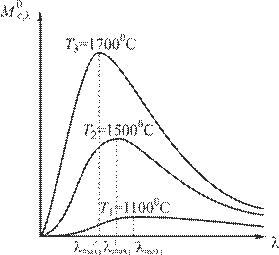Рис. 2.2. Кривая распределения энергии в спектре абсолютно чёрного тела	Рис. 2.3. Кривые спектральной плотности энергетической светимости при различной температуре излучающего тела

Положение максимума спектральной плотноcти энергетической светимости можно определить из выражения (2.13) обычным способом, приравняв к нулю первую производную:

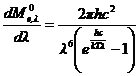
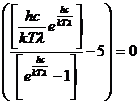. (2.14)

Обозначив 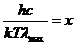, получим:

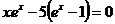. (2.15)

Решение этого трансцендентного уравнения численным методом дает значение 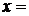4,965.

Следовательно,

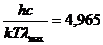, (2.16)

откуда

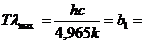2,898· 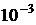м·K, (2.17)

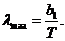(2.18)

где 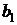– первая постоянная Вина.

Таким образом, функция 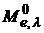достигает максимума при длине волны, обратно пропорциональной термодинамической температуре абсолютно чёрного тела.

Эта зависимость была установлена в 1893 г. немецким физиком Вильгельмом Вином(1864-1928гг.)на основе законовклассической термодинамики и электромагнитной теории света. Её называют законом смещения Вина, подчёркивая тем самым, что с ростом температуры максимум спектральной плотности энергетической светимости сдвигается в сторону меньших длин волн (больших частот).

Из закона Вина следует, что при низких температурах излучаются преимущественно длинные (инфракрасные) электромагнитные волны. По мере же возрастания температуры увеличивается доля излучения, приходящаяся на видимую область спектра, и тело начинает светиться. С дальнейшим ростом температуры яркость свечения увеличивается, а цвет изменяется. Поэтому цвет излучения может служить характеристикой температуры излучения. Примерная зависимость цвета свечения тела от его температуры приведена в табл. 2.1.

Таблица 2.1

Цвет излучения	Красный, едва видимый	Тёмно-красный	Вишнёво-красный	Оранжевый	Белый
Температура, ºС

Подставив формулу (2.18) в выражение (2.13), Вин показал, что максимальное значение функции 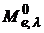пропорционально пятой степени термодинами­ческой температуры тела. Это утверждение носит название второго закона Вина. Он был получен в 1896 году.

Математическое выражение второго закона Вина имеет вид

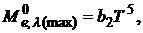(2.19)

где 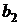– вторая постоянная Вина ( · ).

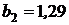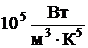В 1911 г. Вильгельм Винбыл удостоен Нобелевской премии по физике за работы по тепловому излучению.

Энергетическую светимость абсолютно чёрного тела можно найти из выражения (2.13) простым интегрированием по длине волны

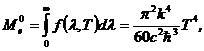(2.20)

где 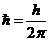– приведённая постоянная Планка,

или

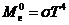(2.21)

где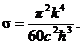

Энергетическая светимость абсолютно чёрного тела пропорциональна четвёртой степени его термодинамической температуры.

Это положение носит название закона Стефана – Больцмана по имени австрийских физиков Й