Уравнение баланса удельных энергий в потоке

Н _ср1 = Н_ср2 + Σh_п,

где Н_ср1 = N₁/Q_G и Н_ср2 = N₂/Q_G ,

Σh_п = N_П/Q_G, - суммарная потеря полного напора на участке между рассматриваемыми сечениями. Записав это уравнение в величинах напора, получим

Уравнение Бернулли для потока вязкой жидкости:

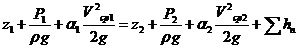(6.8)

От уравнения для элементарной струйки идеальной жидкости это уравнение отличается четвертым членом в правой части - потерей полного напора и коэффициентами Кориолиса, учитывающим неравномерность распределения скоростей. Скорости, входящие в это уравнение, являются средними скоростями в первом и втором сечениях потока.

Это уравнение Бернулли применимо не только для жидкостей, но для газов при условии, что скорость их движения значительно меньше скорости звука.

Графически уравнение можно представить диаграммой (рис.6.4.) подобно уравнению Бернулли для идеальной жидкости с учетом потерь напора. Потери напора вдоль потока возрастают.

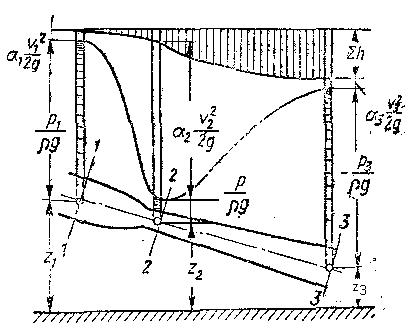
Рис.6.4.Уравнение Бернулли для потока реальной жидкости.

Уравнение Бернулли для струйки идеальной жидкости - это закон сохранения механической энергии.

Уравнение Бернулли для потока реальной жидкости - уравнение баланса энергии с учетом потерь.

Энергия, теряемая жидкостью на рассматриваемом участке течения, превращается в тепловую форму энергии.

Хотя удельная теплоемкость жидкостей велика и тепловая энергия непрерывно рассеивается, повышение температуры рабочей жидкости в гидросистемах бывает значительным. Процесс преобразования механической энергии в тепловую необратим.

Режимы движения жидкости

Разным скоростям потока в трубе одинакового сечения соответствуют разные режимы течения.

При небольших скоростях жидкость движется упорядоченными слоями, при дальнейшем увеличении скорости слои начинают перемешиваться, появляются радиальные составляющие скорости, вихри и режим движения меняется.

Ламинарным режимом движения жидкости называется ее течение упорядоченным слоями без перемешивания.

Турбулентным режимом движения жидкости называется ее течение неупорядоченным слоями с перемешиванием.

При движении жидкости по трубопроводу определенного диаметра с известной шероховатостью существует критическая скорость, при которой режим движения меняется с ламинарного на турбулентный.

Теоретических зависимостей, по которым можно определить Vкр не существует. В конце 19-го века Осборном Рейнольдсом с использованием теории размерности были установлены главные факторы, от которых зависит Vкр =f(d,μ, ρ), это диаметр, вязкость и плотность жидкости.

Размерность скорости[V] и размерность отношения [μ/d*ρ]оказались одинаковыми, а их отношение безразмерно.

.

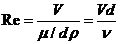где V- средняя скорость потока, d - диа­метр трубы; μ=ρν - динамическая вязкость жидкости, ν- кинематическая вязкость жидкости, ρ - плотность жидкости.

Это отношение называется числом Рейнольдса, его величины получают экспериментально.

Число Рейнольса определяет режим течения жидкости при его значении меньше Re_кр≤2300, режим течения жидкости ламинарный.

Струи жидкости при ламинарном режиме течения, находящиеся на разном удалении от оси движутся с различными скоростями. Наибольшую скорость имеет осевая струйка, на стенках скорость равна нулю.

Увеличение скорости понижает устойчивость ламинарного течения и нарушает его режим. На устойчивость ламинарного режима оказывают влияние1) шероховатость трубы, 2) вязкость жидкости, 3) плотность, 4) скорость движения частиц, 5) диаметр трубопровода.

При перекачивании жидкостей большой вязкости режим течения даже при увеличении скорости может долго оставаться ламинарным.

При увеличении скорости струйки разрываются, разрыву предшествует образование волнообразных колебаний. При усилении колебаний струйка полностью перемешивается с окружающей жидкостью. Движение частиц производит впечатление беспорядочных вихрей. Турбулизация жидкости может произойти даже при вибрации трубопровода. Поскольку есть значение Re_крможно определить соответствующую ему критическую скорость V_кр.

При числах Рейнольдса Re_кр ≤ 2300, движение происходит при ламинарном режиме. Эпюры скоростей ламинарного режима в круглой трубе (рис.6.5а) близки к параболическому закону, коэффициент Кориолиса α=V/Vcp=2-2,1.

При Re>2300-4000 – область перехода от ламинарного к турбулентному режиму, если скорость увеличивать постепенно, можно получить ламинарный режим до Reкр~10⁵.

При числах Рейнольса больше Re>2300 режим течения жидкости становится турбулентным.

Структура потока (рис.6.5б) для турбулентного режима движения состоит из ламинарного подслоя в области близкой к стенке трубы и турбулентного ядра. В подслое даже при увеличении скорости сохраняется ламинарный режим, вязкость жидкости в подслое играет значительную роль в сопротивлении потоку. В турбулентном ядре влияние вязкости незначительно, здесь происходят пульсации скорости и перемешивание частиц жидкости. Эпюры скоростей турбулентного режима в круглой трубе (рис.6.5б) близки к трапеции, коэффициент Кориолиса α=V/Vcp=1-1,1.

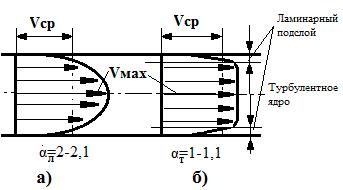
Рис.6.5. Распределение скоростей в круглой трубе,. а) эпюра скоростей ламинарного режима движения, коэффициент Кориолиса α=V/Vcp=2-2,1; б) эпюра скоростей турбулентного режима движения коэффициент Кориолиса α=V/Vcp=1-1,1.