Отличия моделей реальной вязкой жидкости от идеальной.
Динамика вязкой жидкости
Отличия моделей реальной вязкой жидкости от идеальной.
Мощность потока.
Коэффициент Кориолиса.
Энергобаланс потока.
Режимы движения жидкости.
Гидравлические потери: местные и на трение.
Принцип Вентури и его применение.
Отличия реальной (вязкой) жидкости от идеальной.
В идеальной жидкости работа сил, действующих на жидкость, полностью идет на изменение ее кинетической энергии, происходит преобразование кинетической энергии в потенциальную и наоборот.
В реальной жидкости часть работы теряется при преобразовании кинетической энергии в потенциальную из-за наличия сил трения. Возникают потери, эти потери необратимы.
Модель несжимаемой реальной жидкости учитывает влияние вязкости в виде:
1) потерь энергии потока;
2) неравномерности распределения скоростей слоев жидкости по сечению трубопровода.
Уравнения движения вязкой жидкости очень сложны и даже для простейших случаев решаются с помощью численных методов.
Для инженерных задач при изучении движения вязких жидкостей применяется метод усреднения характеристик потока, который позволяет учесть потери энергии, связанные с вязкостью.
При движении вязкой жидкости происходит торможение потока. В эпюре скоростей наибольшие значения достигаются в центральной части потока, а по мере приближения к стенке скорость уменьшается до нуля. Пример распределения скоростей в сечении показан на рис. 6.1.
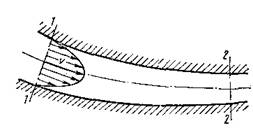
Рис.6.1 Эпюра скоростей в потоке реальной жидкости
Происходит скольжение или сдвиг одних слоев по другим и между слоями возникают касательные напряжения. Движение вязкой жидкости сопровождается вращением частиц, вихреобразованием и перемешиванием.
При движении реальной жидкости преодоление сопротивлений, связанных с вязкостью, требует затрат энергии, поэтому удельная энергия движущейся вязкой жидкости не остается постоянной, как в случае идеальной жидкости, а уменьшается вдоль потока.
Определить мгновенные скорости в различных точках сечения потока реальной жидкости сложно, поэтому рассматривают средние скорости, которые проще измерить.
При выводе уравнения Бернулли для потока реальной вязкой жидкости делают следующие допущения.
Рассматривают средние скорости и средние значения удельной энергии жидкости в данном сечении, то есть проводят осреднение характеристик потока.
Принимают, что в пределах рассматриваемых поперечных сечений потока, справедлив основной закон гидростатики, считают гидростатический напор величиной постоянной для всех точек данного сечения.
Мощность потока
Для усреднения характеристик вводится понятие мощности потока.
Мощность - отношение работы, выполненной за определенный промежуток времени к длительности этого промежутка.
Полная удельная энергии струйки идеальной жидкости или напор в данной точке
Н= z + p/(gρ) + (V2/2g). (6.1)
Элементарный весовой расход
δQG = ρg(V*δS),
V – скорость в сечении δS струйки.
Мощность элементарной струйки равна произведению δN = Н* δQG,
δN = H*δQG = (z + p/ρg + v2/2g)*ρg* V*δS (6.2)
Средний напор - это удельная механическая энергия потока единицы веса в данном сечении
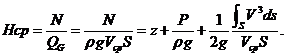
Коэффициент Кориолиса
Умножив и разделив последний член на V 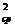 , получим третью степень скорости в знаменателе
, получим третью степень скорости в знаменателе
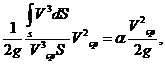 (6.6)
(6.6)
где α – безразмерный коэффициент Кориолиса, учитывающий неравномерность распределения скоростей и равный
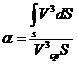 (6.7)
(6.7)
Умножив в этом отношении числитель и знаменатель на ρ/2, получим
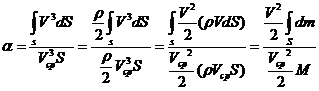
Коэффициентом Кориолиса называется отношение кинетической энергии потока в данном сечении, определенной по действительным скоростям, к кинетической энергии такого же потока, в том же сечения при усредненной скорости и равномерном распределении скоростей, поскольку интеграл 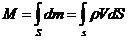 – масса потока в данном сечении.
– масса потока в данном сечении.
Энергобаланс потока
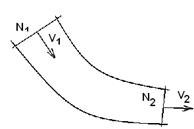
Рис.6.3. Энергобаланс потока
В двух живых сечения потока мощность обозначим, как N1 и N2. Это будет энергия, проносимая потоком через сечения канала S1 и S2 в единицу времени.
Если жидкость невязкая
N1=N2 ,
если жидкость вязкая из-за потерь энергии между сечениями
N1>N2 ,
Разность между значениями мощности в сечениях 1 и 2 это потери на трение или мощность на преодоление гидравлических потерь
NП=N1 - N2.
N1 и N2 характеризуют состояние энергии в сечениях, NП характеризует баланс мощности между сечениями, т.е. потери энергии потока между сечениями.
Поделив величины этого уравнения на весовой расход, получим
Режимы движения жидкости
Разным скоростям потока в трубе одинакового сечения соответствуют разные режимы течения.
При небольших скоростях жидкость движется упорядоченными слоями, при дальнейшем увеличении скорости слои начинают перемешиваться, появляются радиальные составляющие скорости, вихри и режим движения меняется.
Ламинарным режимом движения жидкости называется ее течение упорядоченным слоями без перемешивания.
Турбулентным режимом движения жидкости называется ее течение неупорядоченным слоями с перемешиванием.
При движении жидкости по трубопроводу определенного диаметра с известной шероховатостью существует критическая скорость, при которой режим движения меняется с ламинарного на турбулентный.
Теоретических зависимостей, по которым можно определить Vкр не существует. В конце 19-го века Осборном Рейнольдсом с использованием теории размерности были установлены главные факторы, от которых зависит Vкр =f(d,μ, ρ), это диаметр, вязкость и плотность жидкости.
Размерность скорости[V] и размерность отношения [μ/d*ρ]оказались одинаковыми, а их отношение безразмерно.
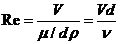 .
.
где V- средняя скорость потока, d - диаметр трубы; μ=ρν - динамическая вязкость жидкости, ν- кинематическая вязкость жидкости, ρ - плотность жидкости.
Это отношение называется числом Рейнольдса, его величины получают экспериментально.
Число Рейнольса определяет режим течения жидкости при его значении меньше Reкр≤2300, режим течения жидкости ламинарный.
Струи жидкости при ламинарном режиме течения, находящиеся на разном удалении от оси движутся с различными скоростями. Наибольшую скорость имеет осевая струйка, на стенках скорость равна нулю.
Увеличение скорости понижает устойчивость ламинарного течения и нарушает его режим. На устойчивость ламинарного режима оказывают влияние1) шероховатость трубы, 2) вязкость жидкости, 3) плотность, 4) скорость движения частиц, 5) диаметр трубопровода.
При перекачивании жидкостей большой вязкости режим течения даже при увеличении скорости может долго оставаться ламинарным.
При увеличении скорости струйки разрываются, разрыву предшествует образование волнообразных колебаний. При усилении колебаний струйка полностью перемешивается с окружающей жидкостью. Движение частиц производит впечатление беспорядочных вихрей. Турбулизация жидкости может произойти даже при вибрации трубопровода. Поскольку есть значение Reкрможно определить соответствующую ему критическую скорость Vкр.
При числах Рейнольдса Reкр ≤ 2300, движение происходит при ламинарном режиме. Эпюры скоростей ламинарного режима в круглой трубе (рис.6.5а) близки к параболическому закону, коэффициент Кориолиса α=V/Vcp=2-2,1.
При Re>2300-4000 – область перехода от ламинарного к турбулентному режиму, если скорость увеличивать постепенно, можно получить ламинарный режим до Reкр~105.
При числах Рейнольса больше Re>2300 режим течения жидкости становится турбулентным.
Структура потока (рис.6.5б) для турбулентного режима движения состоит из ламинарного подслоя в области близкой к стенке трубы и турбулентного ядра. В подслое даже при увеличении скорости сохраняется ламинарный режим, вязкость жидкости в подслое играет значительную роль в сопротивлении потоку. В турбулентном ядре влияние вязкости незначительно, здесь происходят пульсации скорости и перемешивание частиц жидкости. Эпюры скоростей турбулентного режима в круглой трубе (рис.6.5б) близки к трапеции, коэффициент Кориолиса α=V/Vcp=1-1,1.
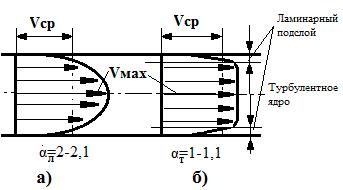
Рис.6.5. Распределение скоростей в круглой трубе,. а) эпюра скоростей ламинарного режима движения, коэффициент Кориолиса α=V/Vcp=2-2,1; б) эпюра скоростей турбулентного режима движения коэффициент Кориолиса α=V/Vcp=1-1,1.
От числа Рейнольдса,
Струйный насос (эжектор)
Состоит из плавно сходящегося насадка, осуществляющего сжатие потока, и постепенно расширяющейся трубки, установленной на расстоянии от насадка в камере.
Скорости потока в струе на выходе насадка увеличивается, в камере давление понижается и возникает разрежение. Под действием разрежения жидкость из нижнего резервуара всасывается по трубе в камеру, где происходят слияние и дальнейшее перемешивание двух потоков. Далее при расширении трубки скорость уменьшается, давление возрастает.
Задача о струйном насосе. Водоструйный насос получает воду под давлением из резервуара А, подсасывает воду из резервуара В на высоту Н1=4 м и нагнетает ее в резервуар С Н2=2м. Выходной диаметр сопла d1=20мм, диаметр смесительной камеры d2= 40мм, выходной диаметр диффузора d3=100мм. Определить минимальный напор h min, при котором насос перестает подсасывать воду из резервуара В. Каков будет при этом расход из сопла? Учитывать потери на расширение в цилиндрической камере и в диффузоре, к-т потерь φд=0,25. Когда насос перестает подсасывать, вакуум составит Н1 м.вод.ст.
1.Расход Q в сечениях 1,2 и 3 связан уравнением неразрывности
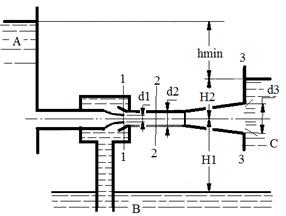
Рис.6.12 Струйный насос
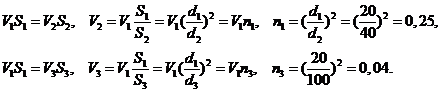
Все скорости в уравнении Бернулли приведены к скорости в сечении 1-1.
2. Уравнение Бернулли для сечений 1 и 3
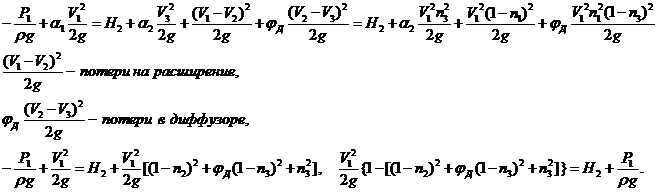 3. Из уравнения Бернулли выражаем скорость
3. Из уравнения Бернулли выражаем скорость
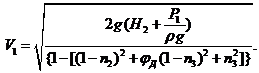
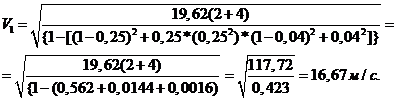
4.Затем находим расход
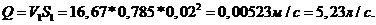
Динамика вязкой жидкости
Отличия моделей реальной вязкой жидкости от идеальной.
Мощность потока.
Коэффициент Кориолиса.
Энергобаланс потока.
Режимы движения жидкости.
