Потери напора, скорость, расход при ламинарном течении. Формула Пуазейля
Потери напора, скорость, расход при ламинарном течении. Формула Пуазейля
Формула Вейсбаха-Дарси.
Начальный участок ламинарного течения
Ламинарное течение в зазоре
Ламинарное течение в зазоре. Случай подвижных стенок.
Ламинарное течение в зазоре. Случай концентрических зазоров.
Потери напора, скорость и расход при ламинарном движении жидкости.
Формула Пуазейля.
При перемещении слоев вязкой жидкости возникают силы внутреннего трения, направленные по касательной к поверхности слоев. Действие этих сил проявляется в разности скоростей слоев (рис.10.1а).
Трение при движении вязкой жидкости было открыто Ньютоном. Он обнаружил пропорциональность между силой внутреннего трения, площадью соприкасающихся слоев и относительной скоростью перемещения.
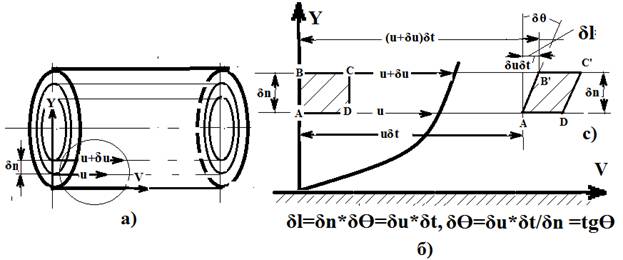
Рис.10.1 Сдвиг слоев реальной жидкости и возникновение деформации сдвига.
При ламинарном режиме в трубе круглого сечения жидкость движется кольцевыми концентрическими слоями ( рис.10.1а) толщиной δn. Скорость слоев уменьшается от стенок к оси. Разность скоростей в соседних слоях равна δu. На поверхности соприкасающихся слоев возникают силы внутреннего трения.
Элементарный объем (рис.10.1б) из-за различия скоростей верхнего и нижнего слоя деформируется, скорость сдвига слоя
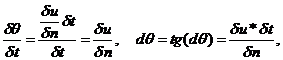
где δu/δn – градиент скорости
Закон внутреннего трения, открытый Ньютоном
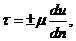(10.1)
где μ – коэффициент динамической вязкости, dθ/dt – скорость деформации сдвига.
В зависимости от направления отсчета от стенки или от оси градиент скорости может быть положительным или отрицательным.
При ламинарном режиме движения слои жидкости скользят один по другому не перемешиваясь. В жидкости преобладают силы вязкости, поэтому силы инерции и силы тяжести при выводах, связанных с ламинарным движением могут не учитываться.
Для определения скоростей, расхода и потерь при ламинарном движении в прямой круглой трубе, расположенной горизонтально, с внутренним диаметром равным d = 2rо,выделяют цилиндрический объем длиной l между сечениями "1-1" и "2-2", радиусом r, соосный с трубой и имеющий основания в выбранных сечениях.
В сечении "1 – 1" давление равно Р1, а в сечении "2 – 2" равно Р2. При одном и том же внутреннем диаметре трубы средняя скорость жидкости будет постоянной V1=V2 , коэффициент Кориолиса α не будет изменяться вдоль потока.
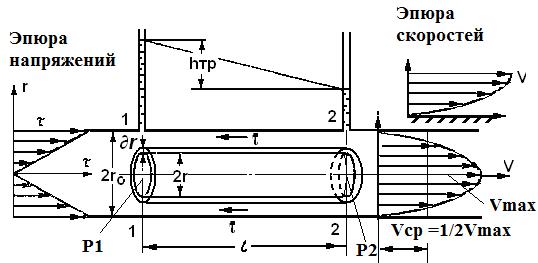
Рис.10.2.Ламинарное движение жидкости в круглой трубе.
Уравнение Бернулли для выбранных сечений "1-1" и "2-2
.
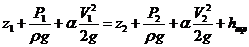При z1=z2, V1=V2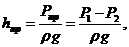 
где hтр = Ртр /(ρg), — потеря напора на трение по длине, эту величину показывают пьезометры, установленные в этих сечениях.
Равновесие выделенного объема рассматривается под действием сил давления и сил трения в слоях окружающей жидкости.
По поверхности цилиндра действуют касательные напряжения τ. При малой длине цилиндра, можно считать, что напряжения равномерно распределенными по поверхности, поэтому уравнение равновесия цилиндра приобретает вид
(Р1 - Р2)πr2-2πrlτ = 0, Ртр *πr2=2πrlτ, откуда
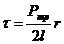. (10.2),
где Ртр =(Р1-Р2) –перепад давлений на основаниях цилиндра.
Касательные напряжения в поперечном сечении трубы изменяются по линейному закону в функции радиуса. Эпюры касательного напряжения показаны на рис.10.2 в начале трубы.
Выразим касательное напряжение τ через динамическую вязкость и градиент скорости, используя радиус r
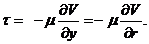
Подставляя τ из уравнения (10.2) , получим
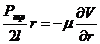
Дифференциал скорости: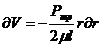 
Выполнив интегрирование, получим мгновенную скорость в любой точке
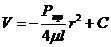
При r = r0 ,V = 0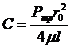 
.
Используя С, получаем
Формула Вейсбаха-Дарси.
Формула потерь на трение для ламинарного режима течения в круглой трубе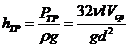 
может быть выражена, как формула Вейсбаха—Дарси.
Подставляя в формулу Дарси среднюю скорость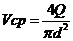 
, группируя и сокращая множители, получим 
значение λ для ламинарного режима движения жидкости в формуле Дарси
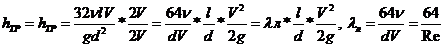
Формула Вейсбаха-Дарси для определения потерь на трение при ламинарном режиме движения жидкости
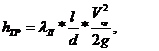(10.8)
где λл =64/Re - коэффициент потерь на трение для ламинарного режима движения
Потери напора, скорость, расход при ламинарном течении. Формула Пуазейля
Формула Вейсбаха-Дарси.