Диффузия в растворах электролитов

Диффузиейназывается процесс самопроизвольного выравнивания химического потенциала в изотермической системе. В случае, если химический потенциал вещества зависит только от его концентрации, диффузия описывается законом Фика:

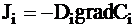, (5 - 1)

где J_i - диффузионный поток вещества i, представляющий собой количество (или массу) вещества, проходящего через единичную поверхность, расположенную перпендикулярно потоку, за единицу времени, gradC_i - градиент концентрации, D_i - коэффициент диффузии, зависящий от типа растворенного вещества, растворителя и температуры.

Знак минус показывает, что диффузионный поток направлен против градиента концентрации, то есть в сторону от высоких концентраций к низким.

Если концентрация изменяется только вдоль одной координатной оси, например, Y, то такая диффузия называется одномерной или линейной. В этом случае закон Фика можно записать в следующей форме:

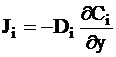. (5 - 2)

Диффузионный поток можно выразить, используя среднюю скорость движения диффундирующих частиц 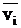. В этом случае поток равен произведению концентрации вещества на среднюю скорость движения частиц:

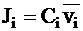. (5 - 3)

Из уравнений (5 - 1) и (5 - 2) для идеальных растворов следует:

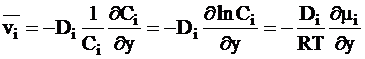. (5 - 4)

Среднюю скорость движения частиц можно рассматривать как величину, зависящую от движущей силы f, приходящейся на одну диффундирующую частицу, и коэффициента сопротивления среды B:

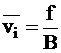. (5 - 5)

Так как движущей силой является градиент химического потенциала, отнесенный к одной частице, то нетрудно найти зависимость коэффициента диффузии предельно разбавленного раствора D⁰_i от коэффициента сопротивления среды:

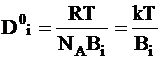. (5 - 6)

Уравнение (5 - 6), в которое входит постоянная Авогадро N_A или постоянная Больцмана, называется уравнением Нернста - Эйнштейна.

Для сферических частиц, имеющих гидродинамический радиус r, коэффициент сопротивления определяется по формуле Стокса:

B = 6phr,

в которой h - вязкость среды. Уравнение (5 - 6) приобретает следующий вид:

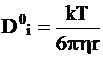. (5 - 7)

Уравнение (5 - 7) называется уравнением Эйнштейна - Стокса.

Для концентрированных растворов используется уравнение, учитывающее влияние молярной доли диффундирующего вещества x_i на коэффициент активности f_i:

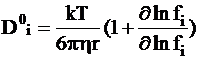. (5 - 7a)

Особенностью диффузии электролитов является то, что различия коэффициентов диффузии ионов приводит к их частичному разделению. В свою очередь пространственное разделение зарядов приводит к скачку потенциала. Таким образом, при диффузии электролитов одновременно действует как собственно диффузионный фактор, так и градиент электрического потенциала gradj. В связи с этим движущей силой диффузии электролитов является не градиент химического потенциала, а градиент электрохимического потенциала.

Электрохимический потенциал ионов i, имеющих заряд z_i, можно выразить через их молярность C_i (см. стр. 113, ч.I данного «Курса»):

.

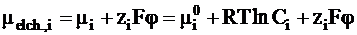В соответствии с основным феменологическим закономтермодинамики необратимых процессов (см. стр. 126, ч. I данного «Курса физической химии») поток ионов i выражается уравнением:

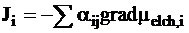. (5 - 8)

Поток ионов можно представить также как сумму двух потоков: диффузионного J_d, определяемого градиентом концентраций, и миграционного J_m, определяемого градиентом электрического потенциала, т.е.

J_i = J_d,i + J_m,i. (5 - 9)

Потоки катионов J_c и анионов J_a для электролита i можно выразить через молярные концентрации и средние скорости движения ионов:

;

.

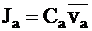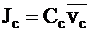На границе двух растворов очень быстро устанавливается такое динамическое состояние, при котором распределение концентраций ионов остается постоянным. Это состояние называется стационарным.

Возникновение стационарного состояния можно объяснить следующим образом.

Если скорость движения одних ионов, например, катионов, больше скорости движения других, то происходит микроскопическое пространственное распределение зарядов, которое упрощенно можно представить как возникновение двух разноименно заряженных обкладок плоского конденсатора. Чем больше различия в скорости движения ионов, тем больше плотность заряда на этих обкладках и тем сильнее они притягиваются друг к другу. Со временем плотность заряда на каждой воображаемой обкладке также возрастает. Наконец, плотность заряда достигает такой величины, что сила электростатического притяжения компенсирует различия в движущей силе диффузии и ионы начинают двигаться с одинаковой скоростью, то есть выполняется условие:

.

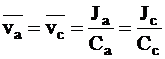Если при диссоциации одной молекулы электролита i образуется n_а анионов и n_с катионов, то поток этого электролита определяется равенством:

.

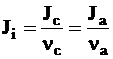Молярную концентрацию этого электролита можно найти из соотношения:

.

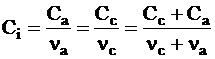Для стационарного состояния из условия общей скорости движения ионов следует:

.

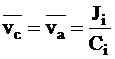Коэффициент диффузии иона можно найти по закону Фика:

.

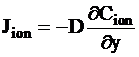Кроме того уравнение Эйнштейна - Стокса можно модифицировать, приняв во внимание следующее.

Коэффициент сопротивления среды B представляет собой отношение силы, вызывающей движение частицы (молекулы или иона), к скорости ее движения. На каждый ион со стороны электрического поля действует сила, равная

,

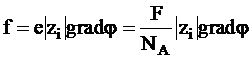где F - постоянная Фарадея, N_A - постоянная Авогадро, z_i - заряд иона в а.е.з.

Коэффициент сопротивления среды можно представить следующим образом:

,

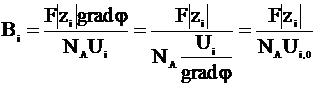где U_i - скорость движения иона, вызываемая электрическим полем, U_i,0 - скорость движения иона при условии, что градиент потенциала равен единице.

Величина U_i,0 называется абсолютной подвижностью иона.

Коэффициент диффузии иона можно выразить следующим образом:

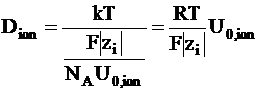. (5 - 10)

Это уравнение называется уравнением Нернста - Эйнштейна.

Уравнение (5 - 10) можно видоизменить для выражения абсолютной подвижности ионов через коэффициент диффузии:

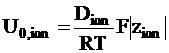. (5 - 11)

Поток ионов при диффузии электролита в целом определяется как диффузионной составляющей, отвечающей уравнению Фика, так и миграционной составляющей, возникающей при градиенте электрического потенциала.

Выразим миграционную составляющую следующим образом:

.

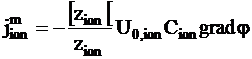С учетом изложенного найдем потоки катионов и анионов:

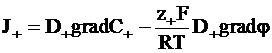; (5 - 12)

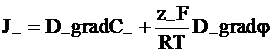. (5 - 12а)

Из равенства скоростей ионов в стационарном состоянии следует:

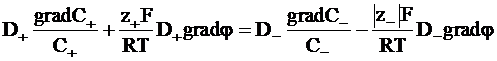. (5 - 13)

Так как C₊=n₊C и C₋=n₋C, то gradC₊/C₊=gradC₋/C₋= gradC/C и из равенства (5 - 13) следует:

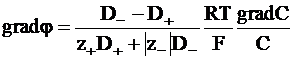. (5 - 14)

Скорость движения ионов окажется равной

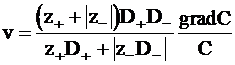. (5 - 15)

Из уравнений (5 -2) - (5 - 4) следует:

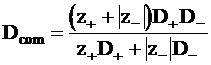. (5 - 16)

D_com является коэффициентом совместной диффузии ионов электролита. Эта величина называется также эффективным коэффициентом диффузии.

Используя, уравнение (5 - 9), D_com можно выразить через абсолютные подвижности ионов:

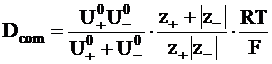. (5 - 17)

Уравнение (5 - 17) называется уравнением Нернста.

Для достаточно концентрированных растворов, которые нельзя считать идеальными, коэффициент диффузии зависит от среднего коэффициента активности g_±:

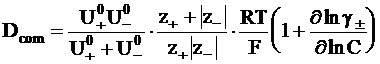. (5 - 18)

Уравнение (5 - 18), используемое для неидеальных растворов, называется уравнением Нернста - Хартли.

Диффузионный потенциал

Скачок потенциала, вызываемый различиями коэффициентов диффузии ионов и возникающий между двумя растворами, называется диффузионным потенциалом.

Для расчета диффузионного потенциала можно воспользоваться уравнением, получаемым интегрированием уравнения (5 ‑ 14). Действительно, из уравнения (5 - 14) следует для одномерного движения частиц (движения вдоль одного координатного направления):

;

;

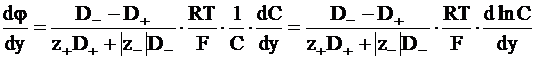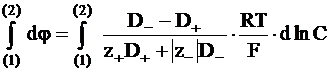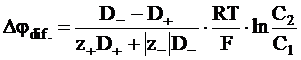. (5 - 19)

Кроме уравнения (5 - 19), для расчета диффузионного потенциала на границе двух растворов можно воспользоваться уравнением, в котором вместо коэффициента диффузии отдельных ионов используются их абсолютные подвижности. Такое уравнение можно получить, используя равенства типа (5 - 11):

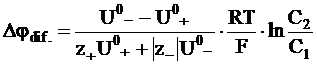. (5 - 20)

Для достаточно концентрированного бинарного электролита вместо концентрации используется активность электролита:

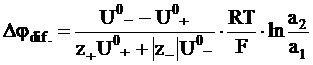. (5 - 21)

Уравнение (5 - 21) является частным случаем более общего уравнения, полученного М. Планком.

Планк разработал квазитермодинамическую теорию диффузионного потенциала.

Основная идея этой теории заключается в предположении, что пространственное разделение зарядов в результате неодинаковой диффузии ионов сопровождается электрической работой.

Если между граничащими растворами взять предельно узкую часть пространства, ограниченную двумя плоскостями, то ей должна соответствовать разность потенциалов, равная dj. Выбрав такую границу, чтобы через плоскости проходил заряд, равный постоянной Фарадея F, найдем, что электрическая работа равна

.

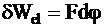В предположении, что разделение зарядов в диффузионном процессе происходит квазистатически (это предположение не соответствует полностью термодинамическим представлениям о квазистатическом процессе и по этой причине теория называется квазитермодинамической), можно принять, что при постоянных Р и Т работа происходит за счет убыли энергии Гиббса:

dW_el = −dG.

Если при переходе от одной плоскости к другой термодинамическая активность i-го вещества изменяется на da_i, то перенос одного моля этого вещества приводит к изменению энергии Гиббса на величину, равную

dG_i⁽¹⁾ = RTdlna_i.

Перенос n_i молей этого вещества приводит к изменению энергии Гиббса на следующую величину:

dG_i = n_iRTdlna_i.

Перенос всех веществ через эти плоскости приводит к полному изменению энергии Гиббса:

.

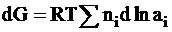Таким образом, скачок потенциала между выбранными плоскостями окажется равным

,

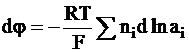а скачок потенциала между двумя растворами, то есть на протяжении всей границы, можно получить как результат интегрирования:

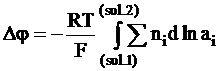. (5 - 22)

Заряд, переносимый данным сортом ионов i, при условии, что заряд одного иона в а.е.з. равен z_i, а число моль ионов равно n_i, будет выражен z_in_i.

Введем новое понятие – число переноса, которое представляет собой переносимую данным сортом ионов долю общего заряда, проходящего по цепи.

В соответствии с этим определением число переноса t_i может быть выражено равенством

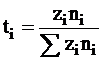. (5 - 23)

Так как было условлено, что суммарный заряд, переносимый по цепи, равен постоянной Фарадея, то в этом случае Sz_in_i = 1, t_i =z_in_i и n_i =t_i/z_i. Следовательно, уравнению (5 - 22) можно придать следующий вид:

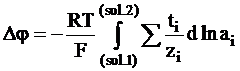. (5 - 24)

Для бинарного электролита число переноса равно отношению абсолютной подвижности данного сорта ионов к сумме абсолютных подвижностей обоих сортов ионов и мы вновь приходим к уравнению (5 - 21).

Экспериментальные данные показывают, что диффузионный потенциал может достигать нескольких десятков милливольт. Таким образом, при расчете стандартных электродных потенциалов может вкрасться серьезная ошибка.

Уравнение (5 - 21) позволяет понять, каким образом можно устранить влияние диффузионного потенциала.

Диффузионный потенциал окажется минимальным, если растворы соединяют солевым мостиком, содержащим концентрированный раствор электролита, образующего ионы с близкими абсолютными подвижностями.