Исследование упругого соударения шаров

Цель работы: экспериментальное определение импульсов двух упруго соударяющихся шаров до и после соударения. Проверка выполнения закона сохранения импульса для замкнутой системы тел.

Теоретическое введение

В физике взаимодействие тел может быть рассмотрено на простейшей модели – центрального удара двух шаров. Удар называется центральным, если шары до удара движутся вдоль прямой, проходящей через их центры.

Существуют два предельных вида удара: абсолютно упругий и неупругий удары. Эти взаимодействия шаров принципиально отличаются друг от друга. При абсолютно неупругом ударе кинетическая энергия движущихся шаров полностью или частично превращается в их внутреннюю энергию (тепло, энергию остаточных деформаций). После удара шары движутся с одинаковой скоростью, как единое целое, либо покоятся. При абсолютно неупругом ударе выполняется только закон сохранения импульса, закон же сохранения механической энергии не соблюдается.

В случае абсолютно упругого удара кинетическая энергия обоих шаров сначала превращается в потенциальную энергию упругих деформаций тел. Затем тела возвращаются к первоначальной форме, отталкивая друг друга. В итоге потенциальная энергия упругих деформаций снова переходит в кинетическую энергию движущихся шаров. При центральном абсолютно упругом ударе выполняются закон сохранения механической энергии и закон сохранения импульса замкнутой системы тел (шаров).

На основе этих законов сохранения можно получить выражение для расчета скоростей шаров после абсолютно упругого удара.

Закон сохранения импульса имеет вид

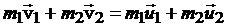, (5.1)

а закон сохранения энергии

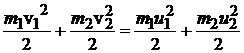(5.2)

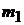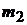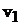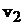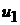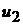где , – массы шаров; и – скорости шаров до удара; и – скорости шаров после удара.

Рассмотрим случай, когда один из шаров массой 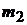до удара неподвижен, т.е. 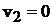. Тогда законы сохранения импульса и механической энергии запишутся в форме:

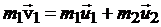, (5.3)

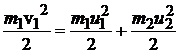. (5.4)

Совместное решение системы уравнений (5.3) и (5.4) (с учетом того, что центры шаров движутся по одной прямой) позволяет определить скорости шаров после удара:

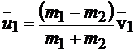, (5.5)

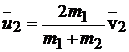. (5.6)

Методика измерений

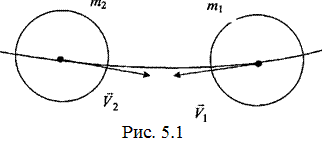В лабораторной работе исследуется центральный упругий удар шаров, когда до удара шары сближаются по линии, проходящей через их центры масс (рис.5.1). Такой удар реализуется в установке с двумя подвешенными на нитях равной длины шарами. Расстояние между точками подвеса равно сумме радиусов обоих шаров.

Пусть левый шар массой 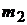до удара покоится. Выведем из положения равновесия правый шар массой 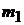на некоторый угол 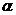и отпустим. Скорости шаров после удара можно определить по углам отклонения 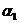и 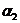первого и второго шаров от положения равновесия.

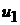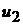Получим рабочие формулы для вычисления скоростей шаров и после удара. Скорость первого шара 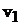до удара определим, используя закон сохранения энергии. Считая, что потенциальная энергия шара массой 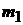, отклоненного на угол 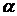, полностью преобразуется в его кинетическую энергию, запишем

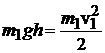(5.7)

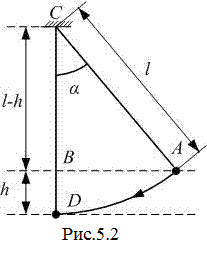
где 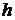– высота подъема шара (рис. 5.2); 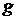– ускорение свободного падения. Как видно из прямоугольного треугольника ABC на рис.5.2,

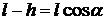. (5.8)

Следовательно,

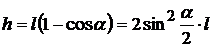(5.9)

Подставляя (5.9) в (5.7), получим: 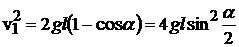, или

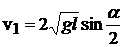(5.10)

Значение скоростей шаров в точке 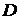непосредственно после удара определяется аналогично по углам отклонения от положения равновесия 1-го (правого) 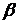и 2-го (левого) шаров :

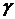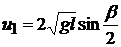(5.11)

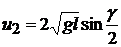, (5.12)

Суммарный импульс системы шаров до первого удара

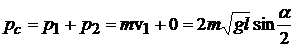(5.13)

После первого удара левый шар получает импульс

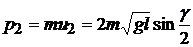, (5.14)

а правый шар останавливается (см. (5.5), ; ) .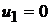

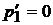Суммарный импульс системы шаров после 1-го удара

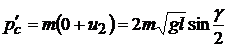(5.15)

После 2-го удара правый шар получает импульс

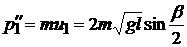, (5.16)

а левый шар останавливается ( ).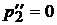

Тогда суммарный импульс системы шаров после 2-го удара

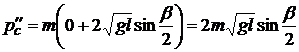(5.17)

Для проверки выполнения закона сохранения импульса необходимо сравнить суммарный импульс системы шаров до и после 1-го и 2-го ударов.

После проведения прямых измерений углов 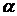, , 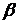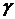следует вычислить по формулам (5.13), (5.15), (5.17) импульс системы шаров до и после ударов, а затем сравнить полученные результаты.

Экспериментальная часть

Приборы и оборудование: экспериментальная установка для изучения центрального удара шаров.

Изучаемый объект представляет собой два одинаковых шара, подвешенных на нитках равной длины. Центры масс шаров лежат в горизонтальной плоскости на расстоянии, равном расстоянию между точками подвеса нитей. Диаметры шаров составляют 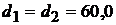мм. Массы шаров 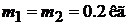. Шары изготовлены из специального полимерного материала. Анализ физико-химических свойств этого полимера позволяет считать, что при соударении шаров условия (5.1) и (5.2) реализуются с хорошей точностью.

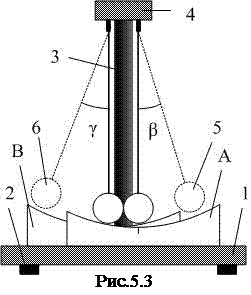Внешний вид установки представлен на рис 5.3. Основание 1 установлено строго горизонтально на лабораторном столе через регулируемые антивибрирующие ножки 2. На верхнем конце штанги 3, закрепленной перпендикулярно основанию, предусмотрен механизм подвеса 4. Он позволяет регулировать длину нитей подвеса шаров 5 и 6 и расстояние между точками подвеса. Для регистрации угловых положений шаров 5 и 6 на основании установлены две шкалы: шкала А – для правого шара 5 и шкала В – для левого шара 6. Таким образом, углы 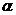и 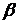фиксируются по шкале А, а угол 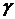– по шкале В.

Правый шар 5 отклоняют вправо на некоторый угол 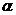и отпускают. Необходимо следить, чтобы шар был расположен точно над шкалой А. Тогда траектория его движения будет лежать в плоскости, где лежат центры масс обоих шаров и обе измерительных шкалы (А и В). Только в этом случае удар будет центральным. Левый шар 6 при этом качнется влево, двигаясь точно над шкалой В. Если по какой-то причине этого не произошло (шар 6 качнулся в сторону), эксперимент следует повторить.