Взаимодействие света с веществом
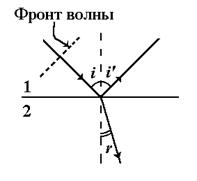 Рис. 8.1.1 Рис. 8.1.1 |
На границе раздела двух прозрачных сред падающая волна расщепляется на две: отраженную и преломленную (рис. 8.1.1). Преломление волны на границе раздела двух сред объясняется тем, что скорости распространения света в средах 1 и 2 различны (и1 и и2 соответственно). Согласно закону преломления
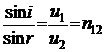 . (8.1.1)
. (8.1.1)
Относительный показатель преломления п12 равен отношению скоростей света в средах.
Для характеристики преломляющих свойств каждой отдельной среды рассматривают преломление при переходе света из вакуума в эту среду. В этом случае и1 = с (скорость света в вакууме), и2 = и и тогда
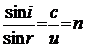 , (8.1.2)
, (8.1.2)
где п ‑ абсолютный показатель преломления среды.
Уменьшение скорости света в диэлектрической среде связано с тем, что под действием электромагнитного поля падающей волны электроны атомов вещества совершают вынужденные колебания и сами становятся источниками электромагнитных волн. Электромагнитное поле волны, распространяющейся в диэлектрике, является результатом суперпозиции поля «исходной» волны и полей, созданных колеблющимися электронами вещества. Поскольку вынужденные колебания всегда отстают по фазе от колебаний вынуждающей силы, то сложение полей приводит к «замедлению» волны в среде в 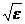 раз (ε - диэлектрическая проницаемость среды). Таким образом, п =
раз (ε - диэлектрическая проницаемость среды). Таким образом, п = 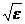 .
.
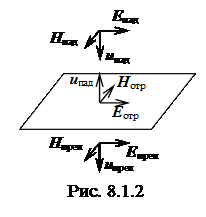 Энергия волны, падающей на границу раздела двух сред, распределяется между отражённой и преломлённой волнами. Рассмотрим нормальное падение световой волны на границу двух сред с абсолютными показателями преломления п1 и п2 (рис. 8.1.2). Условия непрерывности векторов напряжённостей электрического Е и магнитного Н полей имеют вид:
Энергия волны, падающей на границу раздела двух сред, распределяется между отражённой и преломлённой волнами. Рассмотрим нормальное падение световой волны на границу двух сред с абсолютными показателями преломления п1 и п2 (рис. 8.1.2). Условия непрерывности векторов напряжённостей электрического Е и магнитного Н полей имеют вид:
Епад + Еотр = Епрел и Нпад ‑ Нотр = Нпрел.
Используя выражения 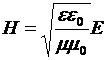 и п =
и п = 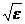 , а также учитывая, что в диэлектрике μ = 1, для амплитуды отражённой волны получим
, а также учитывая, что в диэлектрике μ = 1, для амплитуды отражённой волны получим
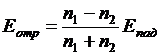 . (8.1.3)
. (8.1.3)
Из этого выражения следует, что при отражении света от оптически более плотной среды (n2 > n1) знак Еотр меняется, что соответствует изменению фазы колебаний вектора Е при отражении на π. В этом случае говорят о «потере полуволны» при отражении.
Коэффициент отражения Rпоказывает, какую долю интенсивности падающей волны Iпад составляет интенсивность волны отражённой Iотр:
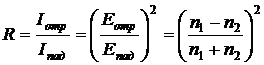 . (8.1.4)
. (8.1.4)
Коэффициент пропускания (прозрачности) Т равен:
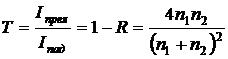 . (8.1.5)
. (8.1.5)
Абсолютный показатель преломления среды зависит от частоты световой волны. Это явление называют дисперсией. Дисперсия объясняется взаимодействием электромагнитной волны с электронами вещества.
Вынужденные колебания электронов атомов вещества под действием электромагнитного поля падающей волны сопровождаются периодическим смещением электронного облака от центра атома 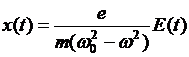 , где ω – частота световой волны, ω0 – собственная частота свободных колебаний электрона в атоме. В результате атом приобретает индуцированный дипольный момент р = е·х, определяющий диэлектрическую проницаемость вещества:
, где ω – частота световой волны, ω0 – собственная частота свободных колебаний электрона в атоме. В результате атом приобретает индуцированный дипольный момент р = е·х, определяющий диэлектрическую проницаемость вещества:
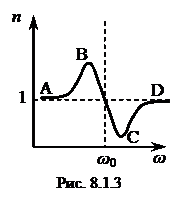
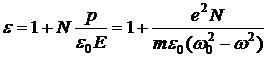 (8.1.6)
(8.1.6)
Показатель преломления вещества равен:
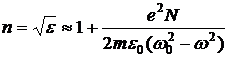 . (8.1.7)
. (8.1.7)
График зависимости n(ω) изображён на рис. 8.1.3. Увеличение показателя преломления с ростом частоты световой волны на участках АВ и СD называют нормальной дисперсией, а уменьшение n на участке ВС – аномальной дисперсией.
Линейно- или плоско-поляризованной называют световую волну, в которой колебания вектора Е происходят в одной фиксированной плоскости. Плоскость, в которой лежат колеблющиеся векторы Е, называют плоскостью поляризации.
Световые волны излучаются при колебании электронных оболочек атомов около ядер. Излучение света атомом происходит в 2 этапа: 1) возбуждение колебаний электронного облака, 2) колебания электронного заряда и испускание световой волны. Длительность одного акта “возбуждение ‒ излучение” очень мала, примерно 10-8 с. Поскольку число излучающих атомов тела очень велико, их излучение никак не согласовано и каждый акт излучения длится очень короткое время, то суммарная световая волна, являющаяся наложением отдельных атомных волн, очень быстро и хаотически меняет направление колебаний вектора E. Такой свет называют неполяризованным или естественным.
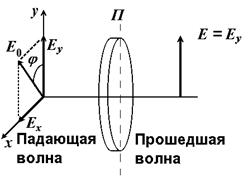 Рис . 8.1.4 Рис . 8.1.4 |
Поляризатором называют устройство, преобразующее естественный свет в поляризованный. Поляризатор П (рис. 4) полностью пропускает волны, поляризованные в y - направлении и полностью поглощает волны, поляризованные в перпендикулярном х - направлении. Направление y называется осью свободного пропускания.
В соответствии с принципом суперпозиции, падающую волну с амплитудой Е0 (рис. 8.1.4) можно представить в виде наложения двух волн, поляризованных в направлениях x и y с амплитудами Ех = Е0 sinj и Еy = E0 cosj.
После прохождения через П волна Ех будет полностью поглощена, следовательно, на выходе Е = Еy = E0cosj. Интенсивность прошедшей волны:
I = I0cos2j (8.1.8)
где I0 - интенсивность падающей волны. Выражение (5) называют законом Малюса.
Интенсивность пучка естественного света после прохождения через идеальный поляризатор уменьшается в два раза: 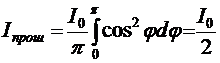 .
.
 При прохождении света через анизотропные среды наблюдается явление двойного лучепреломления. Анизотропия – это неодинаковость физических свойств вдоль различных направлений в среде. Анизотропия характерна для кристаллов.
При прохождении света через анизотропные среды наблюдается явление двойного лучепреломления. Анизотропия – это неодинаковость физических свойств вдоль различных направлений в среде. Анизотропия характерна для кристаллов.
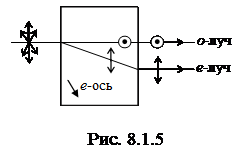
Если на прозрачный кристалл некубической системы направить неполяризованный свет, то внутри кристалла он разделится на два луча, распространяющихся в различных направлениях с разными скоростями (рис. 8.1.5). Один из лучей подчиняется закону преломления, и его называют обыкновенным лучом (о-луч). Ко второму лучу закон преломления не применим, и его называют необыкновенным лучом (е-луч). Эти лучи оказываются полностью поляризованными во взаимно перпендикулярных направлениях.
В ряде кристаллов есть выделенное направление, вдоль которого о- и е-лучи идут с одинаковой скоростью, не разделяясь. Это направление называют оптической осью кристалла (е-ось), а сами кристаллы называют одноосными. Обыкновенный луч поляризован перпендикулярно плоскости, в которой лежат луч и оптическая ось, а необыкновенный луч поляризован в плоскости е-оси.
Интерференция света
Интерференцией называют явление, возникающее при наложении в пространстве двух или нескольких волн одинаковой частоты и поляризации. При этом в некоторых точках пространства волны могут складываться в фазе, и интенсивность суммарной волны I будет больше суммы интенсивностей исходных волн (I > I1 + I2). В других точках пространства волны могут накладываться в противофазе, и интенсивность суммарной волны I будет меньше суммы интенсивностей исходных волн (I < I1 + I2). Устойчивое распределение в пространстве максимумов и минимумов интенсивности, возникающее при наложении двух или нескольких волн, называют интерференционной картиной.
При расчете интерференционной картины следует в каждой точке пространства найти амплитуду суммарного колебания вектора Е, возникающего при сложении колебаний Е1 и Е2, возбужденных в данной точке отдельными электромагнитными волнами. Для этого удобно применять графический метод сложения гармонических колебаний – метод векторных диаграмм.
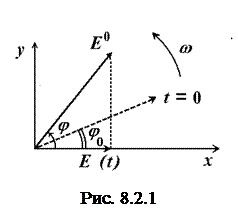 Гармоническое колебание Е(t) задают в виде вектора, равного по длине амплитуде колебания
Гармоническое колебание Е(t) задают в виде вектора, равного по длине амплитуде колебания 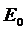 и вращающегося против часовой стрелки с угловой скоростью, равной круговой частоте колебаний w (рис. 8.2.1). Тогда проекция
и вращающегося против часовой стрелки с угловой скоростью, равной круговой частоте колебаний w (рис. 8.2.1). Тогда проекция 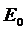 на ось х равна
на ось х равна 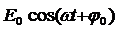 , то есть она описывает гармоническое колебание.
, то есть она описывает гармоническое колебание.
Пусть в точку наблюдения Р приходят две волны одинаковой частоты и поляризации. Они возбуждают колебания:
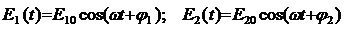 (8.2.1)
(8.2.1)
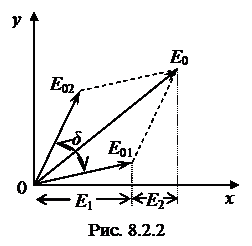 Изобразим их графически с помощью двух вращающихся векторов Е10 и Е20 (рис. 8.2.2). Поскольку w для обеих волн постоянны и одинаковы, то взаимная ориентация Е10 и Е20 в процессе вращения сохраняется. Угол между Е10 и Е20 равен разности фаз колебаний (1):
Изобразим их графически с помощью двух вращающихся векторов Е10 и Е20 (рис. 8.2.2). Поскольку w для обеих волн постоянны и одинаковы, то взаимная ориентация Е10 и Е20 в процессе вращения сохраняется. Угол между Е10 и Е20 равен разности фаз колебаний (1):
d = (wt+j2) - (wt+j1) = j 2- j1. (8.2.2)
Из рис. 8.2.2 видно, что в любой момент времени суммарное колебание равно сумме проекций вращающихся векторов Е10 и Е20. С другой стороны, эта сумма есть проекция вектора Е0, являющегося векторной суммой Е10 и Е20.на диаграмме.
Таким образом, сумма колебаний (8.2.1) с амплитудами Е10 и Е20 эквивалентна колебанию с амплитудой Е0. Амплитуду суммарного колебания находят векторным суммированием векторов Е10 и Е20, повернутых друг относительно друга на угол, равный разности фаз складываемых колебаний d.
Волны, способные при наложении давать устойчивую картину, называют когерентными. Важнейшими условиями когерентности волн являются одинаковость частот и поляризации волн.
Два независимых источника света не могут быть когерентными, поскольку характеристики их излучений, складывающихся из излучений отдельных атомов, меняются хаотически и независимо друг от друга. Для получения двух когерентных световых волн следует получить их от одного источника. Свет, идущий отисточника, нужно разделить на две волны, которые придут в точку наблюдения Р разными путями.
Пусть длины хода двух волн равны l1 и l2. Разность фаз колебаний, создаваемых в точке Р первой и второй волнами, равна:
d = (wt - kl1 + j0) - (wt - kl2 + j0) = k(l2 - l1 ) = kDl = 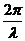 Dl. (8.2.3)
Dl. (8.2.3)
l ‑ длина волны в среде с показателем преломления п. l =l0/n, где l0 - длина волны в вакууме. Следовательно, d = 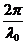 пDl. Величину D = пDl называют оптической разностью хода волн. Окончательно: d =
пDl. Величину D = пDl называют оптической разностью хода волн. Окончательно: d = 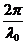 D.
D.
Из векторной диаграммы рис. 8.2.2 видно, что минимум суммарной амплитуды двух волн достигается при
d = p, 3p, 5p, … (2m + 1)p, где m = 0, 1, 2, … (Е10 и Е20 противоположны).
Максимум суммарной амплитуды будет иметь место при
d = 0, 2p, 4p, … m .2p, где m = 0, 1, 2, … (Е10 и Е20 совпадают по направлению).
Условия минимумов и максимумов интерференции можно выразить через оптическую разность хода волн D:
Минимумы: d = 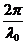 D = (2m + 1)p Þ Dl = (2m + 1)
D = (2m + 1)p Þ Dl = (2m + 1) 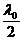 , (8.2.4)
, (8.2.4)
Максимумы:d = 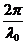 D = m2p Þ Dl = ml0. (8.2.5)
D = m2p Þ Dl = ml0. (8.2.5)
 Рис. 8.2.3 Рис. 8.2.3 |
Рассмотрим явления, возникающие при отражении света от тонкого слоя вещества с показателем преломления п (рис. 8.2.3). В отраженном свете мы будем иметь две волны (1 и 2), отраженные верхней и нижней границами слоя.
При нормальном падении света геометрическая разность хода волн равна удвоенной толщине слоя: Dl = 2d. Оптическая же разность хода равна
D = 2dn +l0/2. (8.2.6)
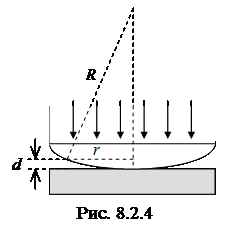 Слагаемое l0/2 учитывает “потерю полуволны” при отражении от поверхности раздела с оптически более плотной средой.
Слагаемое l0/2 учитывает “потерю полуволны” при отражении от поверхности раздела с оптически более плотной средой.
При освещении тонкой плёнки параллельными лучами белого света она приобретает цветную окраску вследствие усиления интенсивности волн с определённой длиной волны, для которых выполняется условие (8.2.5). Разность хода волн при этом должна быть малой (не более ~ 10 мкм), чтобы волны, отраженные верхней и нижней границами плёнки были когерентны.
Частным случаем интерференции света в тонкой плёнке являются так называемые кольца Ньютона. Явление возникает при нормальном падении света на поверхность плосковыпуклой линзы, лежащей на толстой плоскопараллельной стеклянной пластинке (рис. 8.2.4). Роль тонкой плёнки, от поверхностей которой отражаются когерентные волны, играет воздушный зазор между линзой и пластинкой. Вследствие симметрии описанной установки интерференционная картина в монохроматическом свете имеет вид чередующихся темных и светлых концентрических окружностей (колец).
Используя условия (8.2.4) и (8.2.5) максимального усиления и ослабления света в тонкой плёнке, можно получить выражение для радиусов светлых rk и темных rm колец в отраженном свете:
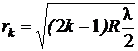 ,
, 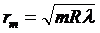 (8.2.7)
(8.2.7)
где k – номер светлого кольца, m – номер светлого кольца, R – радиус кривизны линзы.
Дифракция света
Дифракционные явления возникают при прохождении света через области пространства, содержащие непрозрачные тела, и заключаются в отклонении световых лучей от их первоначального направления.
Задачей теории дифракции является расчет дифракционных картин, т. е. перераспределения светового потока после прохождения света через щели, отверстия известной конфигурации в непрозрачных экранах.
Дифракционная картина возникает следующим образом. Исходная световая волна, падая на тела, возбуждает колебания их электронов. Колеблющиеся электроны сами становятся источниками световых волн. Таким образом, прошедший световой поток складывается из исходной световой волны и из огромного числа волн, испущенных электронными осцилляторами, которые возбуждены в телах исходной волной. Дифракционная картина, следовательно, есть интерференционная картина от очень большого числа волн, испущенных практически непрерывно распределенными источниками.
 Расчет дифракционной картины очень сложен, однако существует удобный расчетный прием, заменяющий строгое решение. Он основан на принципе Гюйгенса – Френеля: каждая точка, до которой дошла волна, становится точечным источником вторичных волн; амплитуда результирующей волны в любой точке пространства является результатом интерференции вторичных волн.
Расчет дифракционной картины очень сложен, однако существует удобный расчетный прием, заменяющий строгое решение. Он основан на принципе Гюйгенса – Френеля: каждая точка, до которой дошла волна, становится точечным источником вторичных волн; амплитуда результирующей волны в любой точке пространства является результатом интерференции вторичных волн.
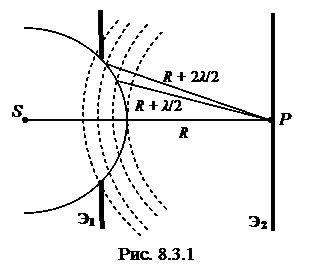
Пусть источник S излучает сферические световые волны (рис. 8.3.1) с длиной волны λ. Чтобы определить интенсивность света в некоторой точке Р, волновую поверхность разбивают на множество кольцевых зон, называемых зонами Френеля. Для этого проводят концентрические сферами с центром в точке P и с радиусами R, 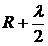 ,
, 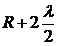 ,
, 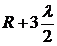 , … . Тогда оптическая разность хода волн, распространяющихся от соседних зон, равна λ/2 и волны складываются в точке Р в противофазе, ослабляя друг друга.
, … . Тогда оптическая разность хода волн, распространяющихся от соседних зон, равна λ/2 и волны складываются в точке Р в противофазе, ослабляя друг друга.
С помощью метода зон Френеля можно объяснить дифракцию от круглого отверстия в непрозрачном экране, а также от круглого диска.
Если установить на пути монохроматической сферической волны непрозрачный экран Э1 с круглым отверстием небольшого размера, как показано на рис. 8.3.1, то на удалённом экране Э2 можно наблюдать дифракционную картину в виде чередующихся светлых и тёмных концентрических колец. В центре картины Р будет светлое круглое пятно, если отверстие открывает нечётное число зон Френеля, и тёмное пятно при чётном числе открытых зон.
Если на пути монохроматической сферической волны поместить небольшой круглый диск, так, чтобы проекция источника волн S на плоскость диска совпадала с центром диска, то на удалённом экране будет возникать дифракционная картина в в виде чередующихся светлых и тёмных концентрических колец. В центре картины всегда будет светлое пятно.
Дифракционной решеткой называется устройство, представляющее собой периодическую структуру из большого числа элементов, на которых происходит дифракция света. Простейшая прозрачная дифракционная решетка представляет собой совокупность большого числа параллельных щелей одинаковой ширины. Расстояние между центрами щелей обозначается d и называется периодом решетки.
 Рис. 8.3.2 Рис. 8.3.2 |
Пусть плоская волна с длиной волны l нормально падает на дифракционную решетку с периодом d (рис. 8.3.2). Каждая щель дает расходящийся пучок света. Для некоторых выделенных направлений, задаваемых углом q, волны от всех щелей будут складываться в фазе и, следовательно, давать максимумы интенсивности. Это условие будет, очевидно, выполнено, если разность хода для волн от двух соседних щелей будет равна целому числу длин волн (рис. 8.3.2):
D = dsinq = ml, m = 0, 1, 2.... (8.3.1)
Формула (8.3.1) называется условием главных максимумов. Число m называют порядком главного максимума. Поскольку при m = 0 q = 0, то для всех волн главный максимум нулевого порядка наблюдается в одном месте - прямо по ходу исходного пучка. При m ¹ 0 каждой длине волны l соответствует свой угол отклонения q, что позволяет использовать дифракционную решетку в качестве спектрального прибора.
Можно показать, что в промежутках между соседними главными максимумами дифракционной картины содержится N - 1 равноотстоящих минимумов, между которыми находятся N - 2 побочных максимума очень малой интенсивности. При достаточно больших N побочными максимумами можно пренебречь.
 Разрешающей способностью дифракционной решётки называют величину
Разрешающей способностью дифракционной решётки называют величину 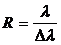 , где Δλ – наименьшая разность длин волн λ1 = λ и λ2 = λ + Δλ, максимумы для которых воспринимаются раздельно. Критерий Рэлея – дифракционные максимумы воспринимаются как раздельные, если минимум одного приходится на максимум другого (рис. 8.3.5).
, где Δλ – наименьшая разность длин волн λ1 = λ и λ2 = λ + Δλ, максимумы для которых воспринимаются раздельно. Критерий Рэлея – дифракционные максимумы воспринимаются как раздельные, если минимум одного приходится на максимум другого (рис. 8.3.5).
Из условия максимумов (1) имеем:
dsinq1 = ml1 = ml и
dsinq2 = ml2 = m(l + Δλ).
Согласно критерию Рэлея угол q2 должен соответствовать минимуму дифракционной картины для l1: dsinq2 = 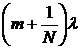 = m(l + Δλ). Следовательно,
= m(l + Δλ). Следовательно,
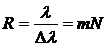 . (8.3.2)
. (8.3.2)
Таким образом, разрешающая способность решётки тем больше, чем выше порядок спектра и чем больше щелей содержит решётка.
9.1 Квантовые свойства
электромагнитного излучения
Тепловое излучение − это электромагнитное излучение оптического диапазона, осуществляемое за счет внутренней энергии тел. Тело, излучающее энергию, будут находиться в состоянии термодинамического равновесия с излучением, если в единицу времени тело будет поглощать столько же энергии, сколько и излучать. Опыт показывает, что тепловое излучение − единственный вид излучения, который может находиться в термодинамическом равновесии с излучающими телами.
Энергетическая светимость (интегральная плотность) потока излучения RТ - энергия, испускаемая в единицу времени единицей поверхности излучающего тела во всём диапазоне частот, по всем направлениям. Энергетическая светимость является функцией температуры.
Испускательная способность тела (спектральная плотность) 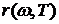 − количество энергии, излучаемой в единицу времени единицей поверхности тела по всем направлениям, в единичном интервале частот. Как и энергетическая светимость, испускательная способность зависит от температуры тела. Энергетическая светимость связана с испускательной способностью соотношением:
− количество энергии, излучаемой в единицу времени единицей поверхности тела по всем направлениям, в единичном интервале частот. Как и энергетическая светимость, испускательная способность зависит от температуры тела. Энергетическая светимость связана с испускательной способностью соотношением:
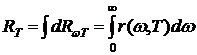 . (9.1.1)
. (9.1.1)
Нагретое тело не только испускает энергию, но и поглощает ее. Поглощательная способность тела а(ω, Т), или спектральный коэффициент поглощения, определяется отношением потока излучения, поглощенного телом в некотором малом интервале частот, к потоку падающего на тело излучения в том же интервале частот: 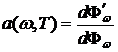 .
.
Абсолютно черное тело (АЧТ) - тело, способное поглощать при любой температуре все падающее на него излучение всех частот. Для абсолютно черного тела поглощательная способность а(ω, Т) ≡ 1.
Между испускательной и поглощательной способностями любого тела, измеренными при одной и той же температуре, имеется связь, устанавливаемая законом Кирхгофа: отношение испускательной и поглощательной способностей не зависит от природы тела, оно является для всех тел одной и той же универсальной функцией частоты (длины волны) и температуры:
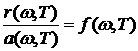 . (9.1.2)
. (9.1.2)
Для абсолютно черного тела по определению а(ω, Т) ≡ 1. Следовательно, для такого тела 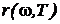 = f(ω, T). Таким образом, универсальная функция Кирхгофа совпадает с испускательной способностью АЧТ. Закон излучения Кирхгофа не распространяется на другие виды излучения.
= f(ω, T). Таким образом, универсальная функция Кирхгофа совпадает с испускательной способностью АЧТ. Закон излучения Кирхгофа не распространяется на другие виды излучения.
Изучение распределения энергии в спектре теплового излучения различных тел при различных температурах привело к установлению эмпирических законов излучения абсолютно черного тела.
Исходя из экспериментальных данных и общих термодинамических соотношений установлено, что энергетическая светимость АЧТ пропорциональна четвертой степени его термодинамической температуры. Эта зависимость называется законом Стефана - Больцмана:
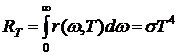 , (9.1.3)
, (9.1.3)
где RТ – энергетическая светимость абсолютно черного тела; σ – постоянная Стефана - Больцмана; T – термодинамическая температура.
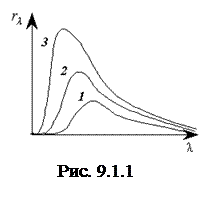 Закон смещения Вина. Распределение энергии в спектре излучения можно характеризовать как зависимостью от частоты излучения, так и зависимостью от длины волны. Закон распределения энергии в спектре излучения АЧТ в зависимости от температуры впервые получен Вином. Согласно этому закону, испускательная способность тела r(λ,Т) возрастает с увеличением длины волны, при некоторой длине волны λm достигает отчетливо выраженного максимума, а затем уменьшается.
Закон смещения Вина. Распределение энергии в спектре излучения можно характеризовать как зависимостью от частоты излучения, так и зависимостью от длины волны. Закон распределения энергии в спектре излучения АЧТ в зависимости от температуры впервые получен Вином. Согласно этому закону, испускательная способность тела r(λ,Т) возрастает с увеличением длины волны, при некоторой длине волны λm достигает отчетливо выраженного максимума, а затем уменьшается.
На рис. (9.1.1) представлены три кривые распределения (1, 2, 3) величины r(λ, Т) ≡ rλ при различных температурах соответственно: Т3 > Т2 > Т1. Согласно закону смещения Вина, с повышением температуры максимум излучения смещается в сторону более коротких волн. Длина волны λm в спектре излучения АЧТ, на которую приходится максимум испускательной способности, определяется по формуле Вина, установленной эмпирическим путем:
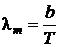 , (9.1.4)
, (9.1.4)
где λm – длина волны, на которую приходится максимум энергии излучения абсолютно черного тела; b – постоянная Вина.
Экспериментально полученное распределение энергии теплового излучения долгое время не удавалось подтвердить теоретически, с использованием классических представлений электромагнитной теории. Если для длинных волн удалось достичь совпадения теоретических результатов с экспериментом, то в области коротких волн (достаточно удаленная ультрафиолетовая область) расчетные значения rλ полностью расходились с экспериментальной кривой. В этом диапазоне теоретическая кривая уходила на бесконечность, и величина энергетической светимости получалась бесконечно большой. Создавшееся положение получило название «ультрафиолетовой катастрофы», которую классическая физика оказалась не в состоянии объяснить.
Решение проблемы было предложено М. Планком, выдвинувшим гипотезу о том, что электромагнитная энергия испускается и поглощается не непрерывно, а отдельными порциями, которые были названы квантами, величина которых пропорциональна частоте излучения. Согласно формуле Планка, энергия отдельного кванта равна:
Е = hν или Е = ħω, (9.1.5)
где h – постоянная Планка (названная так впоследствии); ħ – постоянная Планка, деленная на 2π; ν – частота кванта; ω– циклическая частота.
Исходя из гипотезы о квантовании энергии, Планк получил формулу для испускательной способности АЧТ (закон Планка), точно согласующуюся с экспериментом:
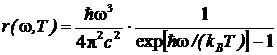 , (9.1.6)
, (9.1.6)
где kB − постоянная Больцмана. 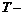 абсолютная температура АЧТ,
абсолютная температура АЧТ, 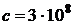 м/с – скорость света в вакууме.
м/с – скорость света в вакууме.
9.2. ФОТОЭФФЕКТ. ЭФФЕКТ КОМПТОНА.
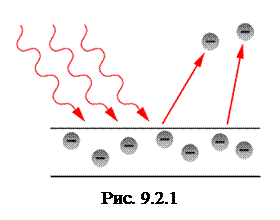 Внешним фотоэффектом называют явление испускания электронов веществом под воздействием света (рис.9.2.1). Электроны, вылетающие из вещества при внешнем фотоэффекте называются фотоэлектронами, а электрический ток, образуемый ими при упорядоченном движении во внешнем электрическом поле, называется фототоком.
Внешним фотоэффектом называют явление испускания электронов веществом под воздействием света (рис.9.2.1). Электроны, вылетающие из вещества при внешнем фотоэффекте называются фотоэлектронами, а электрический ток, образуемый ими при упорядоченном движении во внешнем электрическом поле, называется фототоком.
Испускание электронов может наблюдаться у твердых тел и жидкостей. Практическое значение имеет внешний фотоэффект, наблюдаемый у металлов. В полупроводниках и диэлектриках внешний фотоэффект, как правило, проявляется слабо (хотя в некоторых диэлектрических кристаллах фотоэмиссия достигает высоких значений).
Фотоэффект впервые было обнаружен Герцем в 1887 г и детально исследован профессором Московского университета Столетовым в 1888 г. Многочисленными экспериментами, которые были проведены сразу после открытия фотоэффекта, установлены его основные закономерности:
а) фототок насыщения пропорционален падающему световому потоку при одном и том же спектральном составе излучения;
б) для каждого вещества существует определенная максимальная длина волны света (или минимальная частота), при которой испускание фотоэлектронов прекращается;
в) максимальная кинетическая энергия фотоэлектронов линейно зависит от частоты облучающего света и не зависит от его интенсивности;
г) фотоэффект появляется практически мгновенно, промежуток времени между началом освещения и появлением фототока не превышает 10−9 с.
Перечисленные выше закономерности были совершенно непонятны с позиций классической электромагнитной теории, но оказалось, что все трудности отпадают, если фотоэффект рассматривать с использованием квантовых представлений о природе излучения, предложенных Планком.
Квантовая гипотеза Планка получила дальнейшее развитие в работах Эйнштейна. Представления о квантовом механизме испускания и поглощения электромагнитной энергии Эйнштейн дополнил квантовым механизмом распространения. Им была предложена гипотеза о распространении электромагнитного излучения в виде световых квантов, позднее названных фотонами. Эйнштейн показал, что все особенности внешнего фотоэффекта можно объяснить, если рассмотреть неупругое столкновение фотона с электроном, при котором фотон поглощается электроном. Энергия электрона увеличивается не постепенно, а сразу, в результате единичного столкновения. (Этим объясняется безинерционность фотоэффекта.) Часть этой энергии электрон тратит на выход из металла. Если энергия фотонов, полученная электронами твердого тела, достаточно велика, то они могут достичь поверхности тела и, преодолев потенциальный барьер, выйти за пределы тела. Для каждого материала имеется своя работа выхода А − наименьшая энергия, которую необходимо сообщить электрону, чтобы удалить его из вещества. Работа выхода электронов зависит только от химической природы вещества и состояния его поверхности. Оставшаяся энергия ( hv − А) равна максимальной кинетической энергии фотоэлектрона. Таким образом, весь процесс описывается соотношением, вытекающим из закона сохранения энергии, которое принято называтьуравнением Эйнштейна для фотоэффекта:
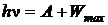 , (9.2.1)
, (9.2.1)
где hν – энергия фотона, падающего на поверхность металла;
Wmax – максимальная кинетическая энергия электрона.
Красная граница внешнего фотоэффекта.С уменьшением частоты падающего света кинетическая энергия фотоэлектронов уменьшается, и может стать равной нулю при некоторой минимальной частоте фотонов ν0 (или максимальной длине волны 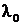 ), тогда фотоэффект прекратится.
), тогда фотоэффект прекратится.
Частота фотонов 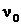 или длина волны
или длина волны 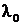 , при которой фотоэффект прекращается, называется «красной границей» фотоэффекта:
, при которой фотоэффект прекращается, называется «красной границей» фотоэффекта:
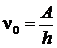 или
или 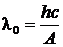 , (9.2.2)
, (9.2.2)
где 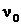 – минимальная частота света, при которой прекращается фотоэффект;
– минимальная частота света, при которой прекращается фотоэффект;
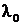 – соответствующая максимальная длина волны.
– соответствующая максимальная длина волны.
Внутренний фотоэффект - увеличение электропроводности веществ под действием света. Наблюдается у некоторых полупроводников и диэлектриков, при этом освобождаемые под действием света электроны не выходят наружу, а, оставаясь внутри тел, увеличивают их электропроводность. Электроны не покидают вещество, а теряют связь с атомами и переходят в свободное состояние, проводимость вещества при этом возрастает.
Приборы, действие которых основано на использовании фотоэффекта называются фотоэлементами.
Фотоэлементы нашли широкое применение в практике: схемы управления и сигнализации, техника кино и телевидения и т.д. Кремневые "солнечные" батареи применяются для питания радиоаппаратуры на искусственных спутниках Земли. На внутреннем фотоэффекте основано действие фотосопротивлений - приборов, сопротивление которых зависит от освещенности.
 Эффект Комптона. Переход от классических представлений к новым квантовым представлениям о природе электромагнитного излучения наиболее полно проявился в объяснении эффекта Комптона. Комптон исследовал рассеяние рентгеновских лучей (длина волны которых примерно в 1000 раз меньше, чем у световых) на атомах легких элементов. Он обнаружил, что в составе рассеянного излучения, наряду с первоначальным излучением с длиной волны λ, наблюдается смещенная линия излучения с бóльшей длиной волны λ0. Возникновение этой линии впоследствии получило название комптоновского смещения. Опыты показали, что разность Δλ = λ0 − λ не зависит от длины волны l падающего излучения и природы рассеивающего вещества, а определяется только углом рассеяния θ, т.е. углом между направлениями первоначального и рассеянного излучения. Объяснить этот эффект исходя из классических представлений не удавалось.
Эффект Комптона. Переход от классических представлений к новым квантовым представлениям о природе электромагнитного излучения наиболее полно проявился в объяснении эффекта Комптона. Комптон исследовал рассеяние рентгеновских лучей (длина волны которых примерно в 1000 раз меньше, чем у световых) на атомах легких элементов. Он обнаружил, что в составе рассеянного излучения, наряду с первоначальным излучением с длиной волны λ, наблюдается смещенная линия излучения с бóльшей длиной волны λ0. Возникновение этой линии впоследствии получило название комптоновского смещения. Опыты показали, что разность Δλ = λ0 − λ не зависит от длины волны l падающего излучения и природы рассеивающего вещества, а определяется только углом рассеяния θ, т.е. углом между направлениями первоначального и рассеянного излучения. Объяснить этот эффект исходя из классических представлений не удавалось.
Тогда Комптон представил этот процесс как рассеяние фотона рентгеновского излучения на свободном покоящемся электроне вещества. Объединив формулу Планка и релятивистское выражение для энергии-массы Эйнштейна 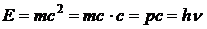 , Комптон получил выражение для импульса фотона:
, Комптон получил выражение для импульса фотона:
 , (9.2.3)
, (9.2.3)
где λ– длина волны фотона.
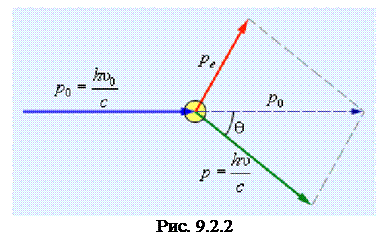
Затем, на основании законов сохранения импульса и энергии в случае упругого столкновения фотона с электроном, получил уравнение для величины разности Δλ в зависимости от угла рассеяния q (см. рис. 9.2.2). Полученное выражение хорошо согласовалось с результатами эксперимента и впоследствии названо формулой Комптона:
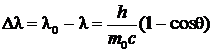 =
= 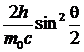 или
или 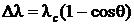 , (9.2.4)
, (9.2.4)
где λ – длина волны фотона, сталкивающегося со свободным электроном;
λ0 – длина волны фотона, рассеянного на угол θпосле столкновения;
m0 – масса покоящегося электрона.
Выражение перед скобками называют комптоновской длиной волны:

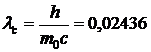 Å. (9.2.5)
Å. (9.2.5)
Таким образом, в объяснении эффекта Комптона квант излучения, предложенный Планком, окончательной обрел все свойства, присущие частицам: кроме энергии у него появился импульс.
По закону сохранения импульса:
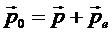 . (9.2.6)
. (9.2.6)
В случае обычного фотоэффекта фотон при встрече с электроном отдает ему всю свою энергию и существование фотона прекращается. При эффекте Комптона фотон отдает электрону часть энергии, т.к. энергия фотона при это уменьшается, то длина волны его увеличивается.
